Univariate beschrijving van de variabelen

In de regel begint men met een univariate inspectie: elke variabele wordt apart onderzocht. Het is absoluut aan te raden om hierbij eerst alle ruwe gegevens te bekijken door middel van grafieken (zie verder) alvorens naar samenvattingsmaten (zoals het gemiddelde) over te stappen. Dit laat toe om een idee te krijgen hoe de geobserveerde waarden van een veranderlijke verdeeld zijn in de studiegroep (bvb. welke verdeling de bloeddrukmetingen in de studie hebben) en of er eventuele uitschieters (d.i. extreme metingen of outliers) zijn. Met outliers worden observaties aangegeven die ten opzichte van de geobserveerde verdeling van de waarden in de data set, extreem zijn, buitenbeentjes.

#De data van de NHANES studie bevindt zich
#in het R package NHANES
library(NHANES) #laad NHANES package

#NHANES is een data frame met de gegevens
#De rijen bevatten informatie over elk subject
#De kolommen de variabelen die werden geregistreerd
#vb variabele Gender, BMI, ...
#Een variabele (kolom) kan uit de dataframe
#worden gehaald door gebruik van het $ teken
#en de naam van de variabele
# We slaan de frequentietabel voor variable Gender
# op in object 'tab'

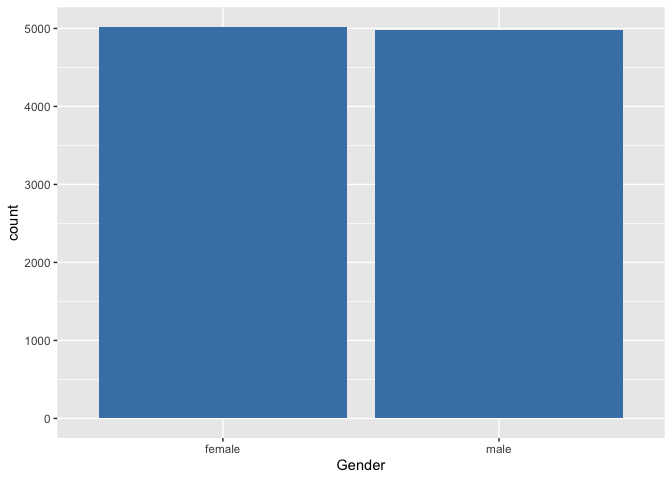
tab <- table(NHANES$Gender)
tab

## 
## female   male 
##   5020   4980

We maken nu een barplot voor de variabele gender

We pipen de NHANES data naar ggplot
Als aestetics definiëren we x=Gender
We voegen een laag met een barplot toe via de functie geom_bar. We definiëren de kleur via het argument fill

NHANES %>%
  ggplot(aes(x=Gender)) +
  geom_bar(fill="steelblue")

Er zijn weinig methoden voorhanden om nominale variabelen te beschrijven. In Voorbeeld 19 is de variable Gender kwalitatief nominaal. Alles is gezegd over de verdeling van het geslacht als we weergeven hoeveel vrouwen en mannen zijn opgenomen in de studie.

We stellen vast dat 5020 van de 10000 subjecten, ofwel 50.2% vrouwen in de studie zijn opgenomen.

Een staafdiagram geeft op de X-as de mogelijke uitkomsten van de variabele aan (bvb. geslacht). Daarbovenop komt een staaf met hoogte evenredig aan het totaal aantal keer dat die waarde voorkomt in de dataset. De staven staan los van elkaar met een breedte die constant is, maar verder willekeurig. Als de steekproef representatief is voor de populatie, dan krijgen we hier misschien een eerste impressie dat er iets meer vrouwen zijn in de populatie.

Voor numerieke continue variabelen wordt het moeilijk om de frequentie van alle uitkomstwaarden in een tabel te klasseren omdat veel waarden hoogstens 1 keer voorkomen. Het tak-en-blad diagram (in het Engels: stem and leaf plot is een middel om toch nog alle uitkomsten weer te geven. Een voorbeeld is weergegeven in onderstaande R-output voor het BMI in de NHANES studie.

stem(NHANES$BMI)

## 
##   The decimal point is 1 digit(s) to the right of the |
## 
##   1 | 33333333333333333344444444444444444444444444444444444444444444444444+37
##   1 | 55555555555555555555555555555555555555555555555555555555555555555555+1389
##   2 | 00000000000000000000000000000000000000000000000000000000000000000000+2264
##   2 | 55555555555555555555555555555555555555555555555555555555555555555555+2610
##   3 | 00000000000000000000000000000000000000000000000000000000000000000000+1693
##   3 | 55555555555555555555555555555555555555555555555555555555555555555555+635
##   4 | 00000000000000000000000000000000000000000000000000000000000000000000+255
##   4 | 55555555555555555555555556666666666666666666666666666666666777777777+46
##   5 | 0000011111122222233333444444444444
##   5 | 5556677777789999
##   6 | 133444
##   6 | 567899
##   7 | 
##   7 | 
##   8 | 111

Hier wordt van alle uitkomsten het eerste cijfer of de eerste paar cijfers op een verticale lijn in volgorde uitgezet in de vorm van een boomstam. Daaraan worden horizontaal de bladeren gehecht, met name de laatste cijfers van de geobserveerde uitkomsten. De output geeft bijvoorbeeld aan dat er 3 personen zijn waarvan het afgeronde BMI 55 bedraagt, 2 personen met een afgerond BMI van 56, …. Gezien de studie zo groot is, is het tak-en-blad diagram niet erg praktisch voor dit voorbeeld.

In een tak-en-blad diagram krijgt men alle individuele uitkomsten nagenoeg exact te zien, terwijl de vorm die het diagram aanneemt reeds een idee van de verdeling geeft zoals in een histogram (zie verder). Een vuistregel om de vorm van de verdeling het best te zien is het aantal takken ongeveer gelijk te maken aan \(1 + \sqrt{n}\), waarbij \(n\) het aantal observaties voorstelt. Dit aantal kan uiteraard aangepast worden aan de omstandigheden. Een populair alternatief voor het tak en blad diagram is de eenvoudige frequentietabel. Deze kan men bekomen door de continue variabele (bvb. BMI) om te zetten in een kwalitatieve ordinale variabele, waarvoor vervolgens een frequentietabel wordt weergegeven.

Het grafisch equivalent van dergelijke frequentietabel noemt een histogram, hetgeen men in ggplot bekomt via

Pipe de data van de NHANES study naar de ggplot functie
Selecteer de variable BMI als de data om in de x-coordinaat te visualiseren voor het aestetics argument van ggplot gebruik hiervoor de aes functie
Voeg een laag toe voor het histogram. Wanneer je geen aestetics aes meegeeft verkrijg je standaard absolute frequenties. Met fill=..counts.. in de aestetics kan je de balken van het histogram inkleuren a.d.h.v. de absolute frequenties.
Indien je het wenst kan je op een histogram met densities ook nog een laag toevoegen met een niet parametrische densiteitsschatter voor de verdeling d.m.v. de geom_density functie.

NHANES %>%
  ggplot(aes(x=BMI)) +
  geom_histogram(aes(y=..density.., fill=..count..),bins=30) +
  geom_density()

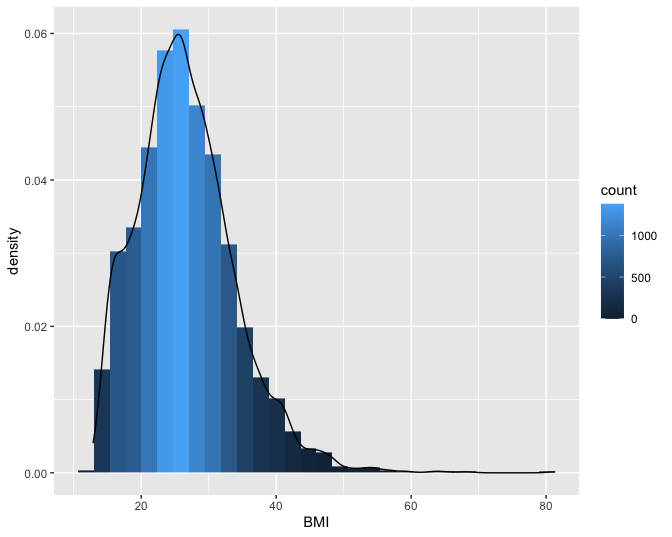
Figuur 5: Histogram van het BMI in de NHANES studie.

Wanneer alle klassen een zelfde breedte hebben, worden de absolute of relatieve frequenties per klasse weergegeven door de hoogte van de bijhorende kolom. Bij ongelijke klassebreedtes is het de oppervlakte van de kolom die met de bijhorende klassefrequentie correspondeert. Omdat een histogram met ongelijke klassebreedtes moeilijker te interpreteren is, zijn histogrammen met gelijke klassebreedtes vaak te verkiezen. Als histogrammen voor verschillende groepen bekeken worden, vergemakkelijkt het gebruik van relatieve frequenties i.p.v. absolute frequenties de visuele vergelijkbaarheid.

Op het histogram in Figuur 5 worden densiteiten weergegeven en klassen met een breedte iets meer dan 5 eenheden.

De keuze van het aantal klassen is van belang bij een histogram. Als er te weinig klassen zijn, dan gaat veel informatie verloren. Als er teveel zijn, dan wordt het algemene patroon verdoezeld door een grote hoeveelheid overbodige details. Gewoonlijk kiest men tussen 5 en 15 intervallen, maar de specifieke keuze hangt af van het beeld van het histogram dat men te zien krijgt.

Een histogram is vooral geschikt om de distributie te schatten in grote datasets. Daar kan men dan veel intervallen gebruiken. Daarom heeft de ggplot functie standaard 30 intervallen.

Indien een voldoende aantal gegevens beschikbaar is, dan kan men een gladdere indruk van de verdeling van de gegevens bekomen door een zogenaamde kernel density schatter te bepalen. Zo’n schatter is een positieve functie die genormaliseerd is in die zin dat de oppervlakte onder de functie 1 is. Ze kan zo geïnterpreteerd worden dat de oppervlakte onder de functie tussen 2 punten \(a\) en \(b\) op de X-as, de kans voorstelt dat een lukrake meting in het interval \([a,b]\) gevonden wordt. Figuur 5 toont een histogram met kernel density schatter van de het BMI.

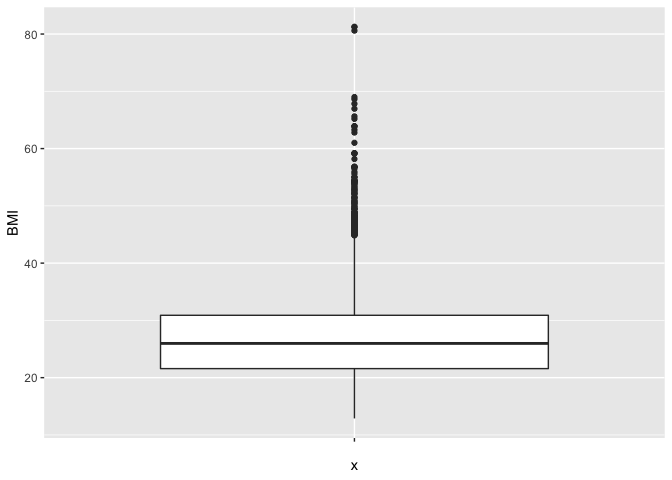
De verdeling kan ook geëvalueerd worden aan de hand van een box-and-whisker-plot, kortweg boxplot genoemd. Deze is meer compact dan een histogram en laat om die reden gemakkelijker vergelijkingen tussen verschillende groepen toe (zie verder). Een Boxplot voor het BMI wordt getoond in Figuur 6. De boxplot toont een doos lopend van het 25% tot 75% percentiel met een lijntje ter hoogte van de mediaan (het 50% percentiel) en verder 2 snorharen. Die laatste kunnen in principe lopen tot het minimum en maximum, of tot het 2.5% en 97.5 % of 5% en 95% percentiel. R kiest voor de kleinste en de grootste geobserveerde waarde die geen outlier of extreme waarde zijn. Een meting wordt hierbij een outlier genoemd wanneer ze meer dan 1.5 keer de boxlengte beneden het eerste of boven het derde kwartiel ligt. Een meting wordt een extreme waarde genoemd wanneer ze meer dan 3 keer de boxlengte beneden het eerste of boven het derde kwartiel ligt.

Definitie 10 (percentiel)

Het 25% percentiel of 25% kwantiel \(x_{25}\) van een reeks waarnemingen wordt gedefinieerd als een uitkomstwaarde \(x_{25}\) zodat minstens \(25\%\) van die waarnemingen kleiner of gelijk zijn aan \(x_{25}\) en minstens \(75\%\) van die waarnemingen groter of gelijk zijn aan \(x_{25}\). Het 75% percentiel of 75% kwantiel van een reeks waarnemingen definieert men als een uitkomstwaarde \(x_{75}\) zodat minstens 75% kleiner of gelijk zijn aan \(x_{75}\) en minstens \(25\%\) van die waarnemingen groter of gelijk zijn aan \(x_{75}\). Algemeen wordt het \(k\%\) percentiel van een reeks waarnemingen gedefinieerd als een waarde (van \(x\)) waarvoor de cumulatieve frequentie gelijk is aan \(k/100.\) Als er meerdere observaties aan voldoen neemt men vaak het gemiddelde van die waarden.

Einde definitie

In R kunnen die als volgt worden bekomen

quantile(NHANES$BMI,c(0.25,.5,.75),na.rm=TRUE)

##   25%   50%   75% 
## 21.58 25.98 30.89

Figuur 6: Boxplot van BMI in de NHANES studie.

In ggplot maak je de boxplot als volgt:

NHANES %>%
  ggplot(aes(x="",y=BMI)) +
  geom_boxplot()

Bij de inspectie van een dataset speelt het detecteren van outliers in het algemeen een belangrijke rol. Ze kunnen wijzen op fouten, zoals tikfouten of andere fouten die gecheckt en gecorrigeerd moeten worden. Als het geen foutief genoteerde waarden zijn, dan kan het soms wijzen op een subject dat niet echt in de studiepopulatie thuis hoort. Als het in alle opzichten om een bona fide waarde gaat, dan nog is het belangrijk om outliers te detecteren: ze kunnen zeer invloedrijk zijn op de schatting van statistische parameters (zie Sectie 4.3). Als de conclusies van een studie anders liggen met of zonder inclusie van de outlier, dan is dit een ongewenst fenomeen. Men wil immers nooit dat 1 observatie beslissend is voor de conclusies. Dit soort onzekerheid ondermijnt de geloofwaardigheid van de onderzoeksresultaten en vraagt om verdere studie. Binnen de statistiek bestaat een grote waaier aan technieken, zogenaamde robuuste statistische technieken, die erop gericht zijn om de invloed van outliers te minimaliseren. In deze cursus gaan we hier slechts in zeer beperkte mate op in (zie Sectie 4.3, mediaan).