In general, instead of arbitrarily choosing \(\lambda = 4\), it would be better to use cross-validation to choose the tuning parameter \(\lambda\). We can do this using the built-in cross-validation function, cv.glmnet(). By default, the function performs ten-fold cross-validation, though this can be changed using the argument folds. Note that we set a random seed first so our results will be reproducible, since the choice of the cross-validation folds is random.

> set.seed(1)
> cv.out <- cv.glmnet(x[train,], y[train], alpha = 0)
> plot(cv.out)
> bestlam <- cv.out$lambda.min
> bestlam
[1] 326.0828

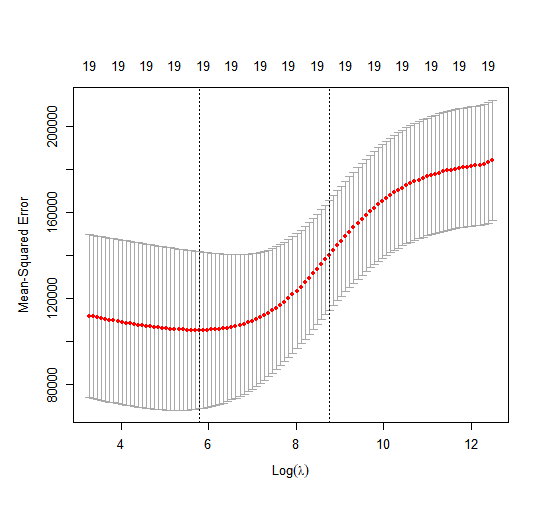
Therefore, we see that the value of \(\lambda\) that results in the smallest cross-validation error is 326. What is the test \(MSE\) associated with this value of \(\lambda\)?

> ridge.pred <- predict(ridge.mod, s = bestlam, newx = x[test,])
> mean((ridge.pred - y.test)^2)
[1] 139856.6

This represents a further improvement over the test \(MSE\) that we got using \(\lambda\) = 4. Finally, we refit our ridge regression model on the full data set, using the value of \(\lambda\) chosen by cross-validation, and examine the coefficient estimates.

> out <- glmnet(x, y, alpha = 0)
> predict(out, type = "coefficients", s = bestlam)[1:20,]
 (Intercept)        AtBat         Hits        HmRun 
 15.44383135   0.07715547   0.85911581   0.60103107 
        Runs          RBI        Walks        Years 
  1.06369007   0.87936105   1.62444616   1.35254780 
      CAtBat        CHits       CHmRun        CRuns 
  0.01134999   0.05746654   0.40680157   0.11456224 
        CRBI       CWalks      LeagueN    DivisionW 
  0.12116504   0.05299202  22.09143189 -79.04032637 
     PutOuts      Assists       Errors   NewLeagueN 
  0.16619903   0.02941950  -1.36092945   9.12487767 

As expected, none of the coefficients are zero, ridge regression does not perform variable selection!

Using the Boston dataset, try determining the lambda that minimizes the \(MSE\) (store it in bestlam) using the cross-validation approach (store the cross-validation output in cv.out). With the acquired \(\lambda\), determine the ridge regression predictions (store them in ridge.pred) and calculate the \(MSE\) (store it in ridge.mse).

---

Assume that:

• The MASS and glmnet libraries have been loaded
• The Boston dataset has been loaded and attached
• The seed is set on 1.
• The variables x, y created in exercise Ridge Regression 1¹ are already loaded
• The variables train, test, y.test and ridge.mod created in exercise Ridge Regression 4² are already loaded