ShellSort, genoemd naar zijn uitvinder D.L. Shell, is een sorteeralgoritme dat een rij sorteert door herhaaldelijk een ander sorteeralgoritme toe te passen op verscheidene door elkaar geweven deelrijen van de gegeven rij. Ondanks zijn tijdscomplexiteit met bovengrens \(O(n^2)\), zal ShellSort (mits goed gekozen deelrijen en intern algoritme) zijn ondergrens \(\Omega(n \log n)\) sterk benaderen.

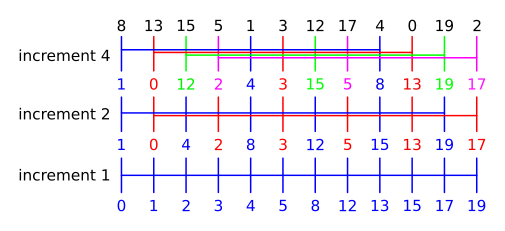
Het bepalen van de deelrijen gebeurt als volgt: in elke fase \(i\) van het algoritme wordt de deelrij gevormd door het doorlopen van de rij met een increment van \(h_i\). De reeks van gebruikte incrementen moet dalend zijn en moet eindigen met \(1\), m.a.w. \(h_1 > \cdots > h_i > \cdots > h_m = 1\). De efficiëntie van het algoritme is sterk afhankelijk van de incrementreeks, met \((1, 4, 13, 40, 121, \dots)\) gekend als één van de beste incrementreeksen.

Zoals vermeld werkt ShellSort met een intern sorteeralgoritme. Hiervoor worden vaak (varianten op) eenvoudige algoritmen als BubbleSort en InsertionSort gebruikt. Belangrijk: om als “goed” intern sorteeralgoritme te kwalificeren, dient het gekozen algoritme (bijna) lineair te presteren op een (bijna) gesorteerde rij.

Opgave

Schrijf een Python-functie shellsort(rij: list, incrementen: list) die de gegeven rij sorteert gebruik makende van het ShellSort-algoritme. De incrementen die gebruikt moeten worden, worden als tweede parameter aan de functie meegegeven. Na het uitvoeren van de functie moet de originele lijst aangepast zijn. Het is enkel toegelaten om elementen uit de lijst te vervangen. Je mag dus geen elementen verwijderen of toevoegen.

Voorbeelden

>>> rij = [8, 13, 15, 5, 1, 3, 12, 17, 4, 0, 19, 2]
>>> shellsort(rij, incrementen = [4])
>>> rij
[1, 0, 12, 2, 4, 3, 15, 5, 8, 13, 19, 17]
>>> rij = [8, 13, 15, 5, 1, 3, 12, 17, 4, 0, 19, 2]
>>> shellsort(rij, incrementen = [4, 2, 1])
>>> rij
[0, 1, 2, 3, 4, 5, 8, 12, 13, 15, 17, 19]