De wortelformule¹ is de algemene methode om een vierkantsvergelijking op te lossen. In deze opdracht ga je dit implementeren in Python code.

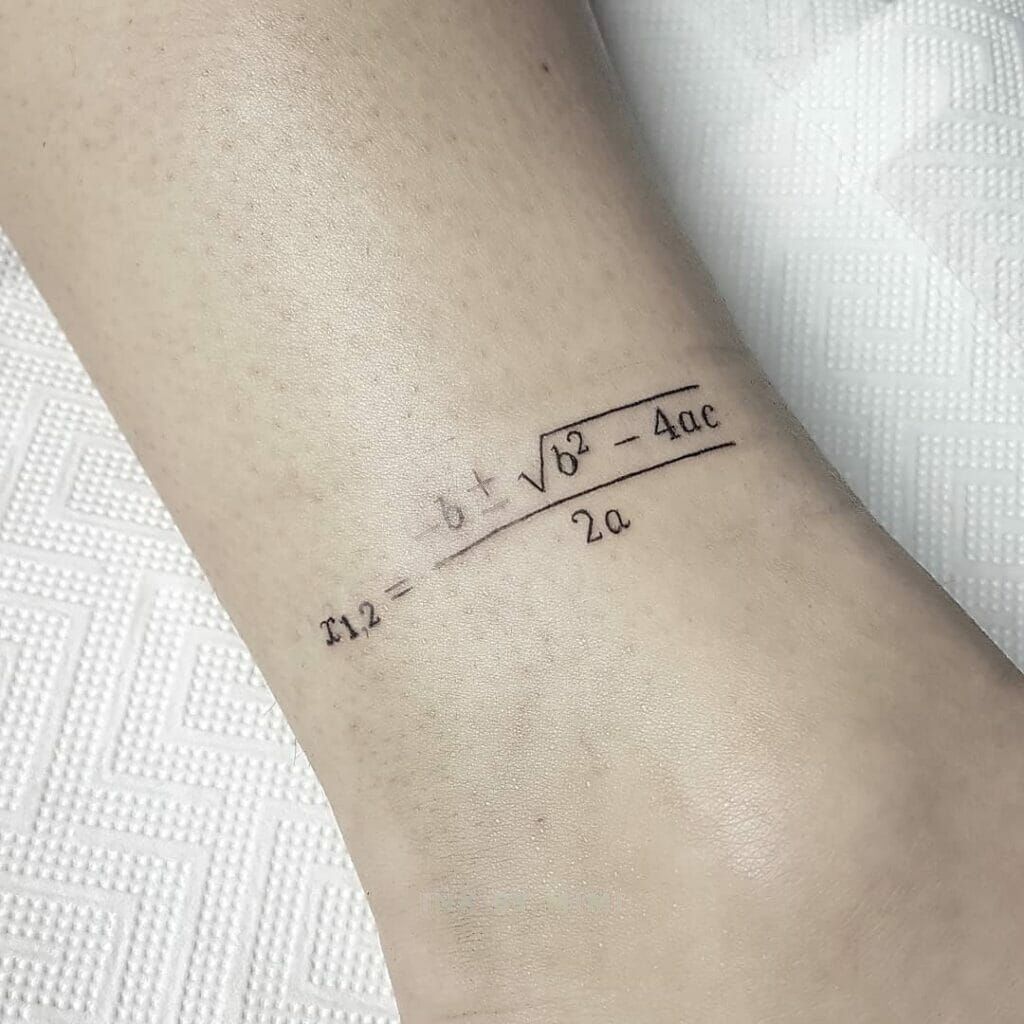
Opgave

Schrijf een programma dat van een vierkantsvergelijking (in de algemene vorm) \(\mathsf{ax^2+bx+c=0}\) achtereenvolgens de waarden van de coëfficienten \(\mathsf{a}\), \(\mathsf{b}\) en \(\mathsf{c}\) vraagt.

Daarna wordt, indien mogelijk, de oplossingenverzameling berekend. De mogelijke oplossingen worden op een specifieke manier weergegeven, de kleinste oplossing komt steeds eerst. Het resultaat wordt afgerond op twee cijfers na de komma.

Voorbeelden

De vierkantsvergelijking \(\mathsf{x^2+3x-4 = 0}\) heeft als oplossingenverzameling \(\mathsf{V = \{-4, 1\}}\).

Er zijn twee verschillende reële oplossingen, namelijk -4.0 en 1.0

De vierkantsvergelijking \(\mathsf{x^2+2x+1 = 0}\) heeft als oplossingenverzameling \(\mathsf{V = \{-1\}}\).

Er is exact één reële oplossing, namelijk: -1.0

De vierkantsvergelijking \(\mathsf{2x^2+6x+5 = 0}\) heeft geen reële oplossingen.

Er zijn geen reële oplossingen.