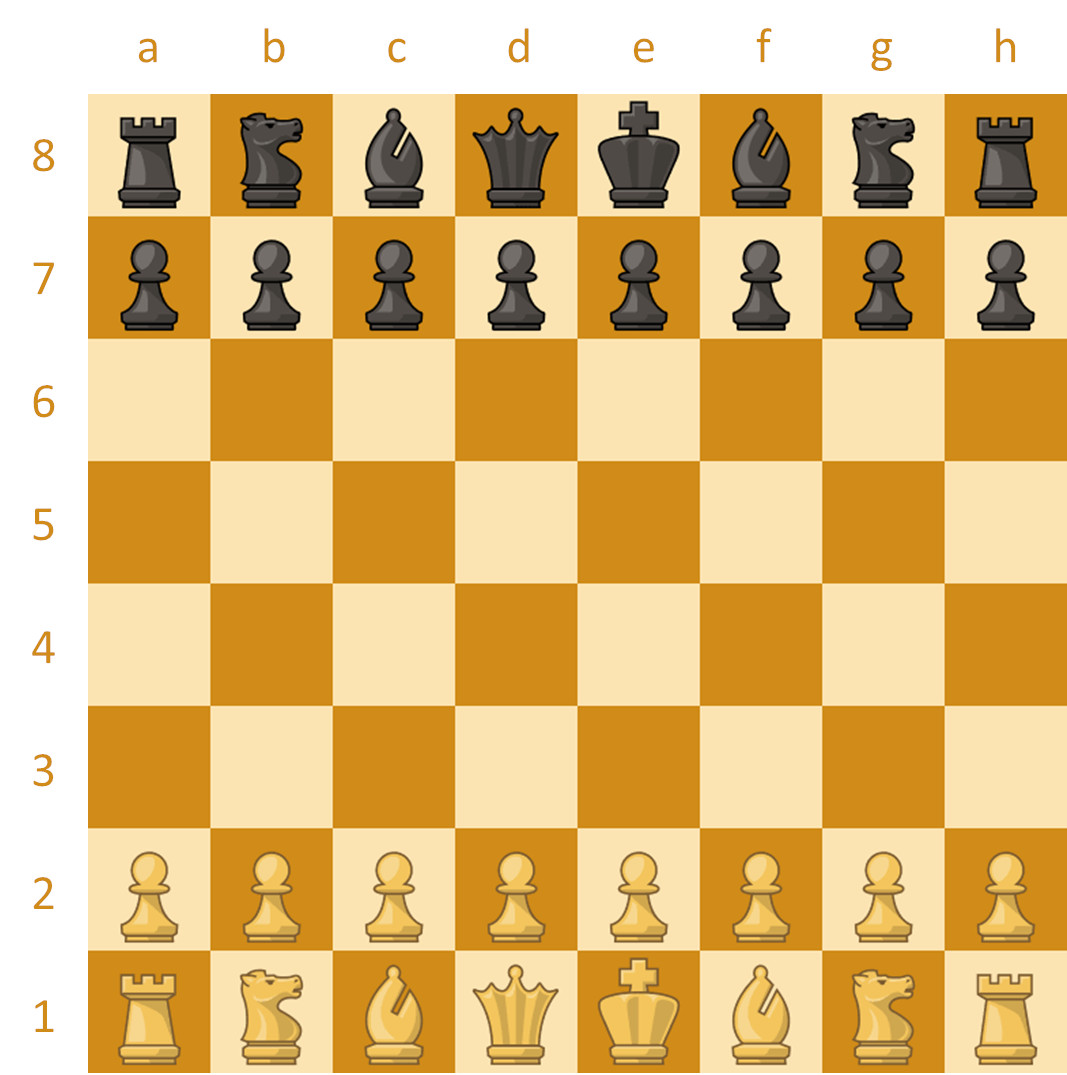
Bij schaken wordt gebruikgemaakt van een schaakbord: een vierkant spelbord dat wordt opgedeeld in 32 lichte en 32 donkere velden die elkaar afwisselen. De horizontalen worden rijen genoemd en zijn genummerd van 1 tot en met 8. De verticalen worden lijnen genoemd en worden aangegeven met de letters a tot en met h. Op die manier kan elk veld aangeduid worden door de combinatie van een letter en een cijfer: de witte koningin staat bijvoorbeeld in de beginstelling op d1. Het bord wordt zo neergelegd dat a1 en h8 — de hoekvelden links van de spelers — zwart zijn.

Elke speler beschikt over zestien speelstukken: 1 koning (king, K), 1 koningin (queen, Q), 2 torens (rook, R), 2 lopers (bishop, B), 2 paarden (knight, N) en 8 pionnen (pawn, P). De ene speler heeft witte speelstukken, de andere heeft zwarte speelstukken. Bij aanvang van het spel staan de speelstukken op de volgende manier op het bord.

Forsyth-Edwards Notation of FEN is een standaard voor het beschrijven van de opstelling van de speelstukken op een schaakbord. Het is gebaseerd op een systeem dat in de 19e eeuw werd ontwikkeld door de Schotse journalist David Forsyth, en dat later door Steven J Edwards werd uitgebreid zodat het kon gebruikt worden in computerprogramma's. Zo wordt bijvoorbeeld de beginopstelling van de speelstukken in FEN genoteerd als

rnbqkbnr/pppppppp/8/8/8/8/PPPPPPPP/RNBQKBNR

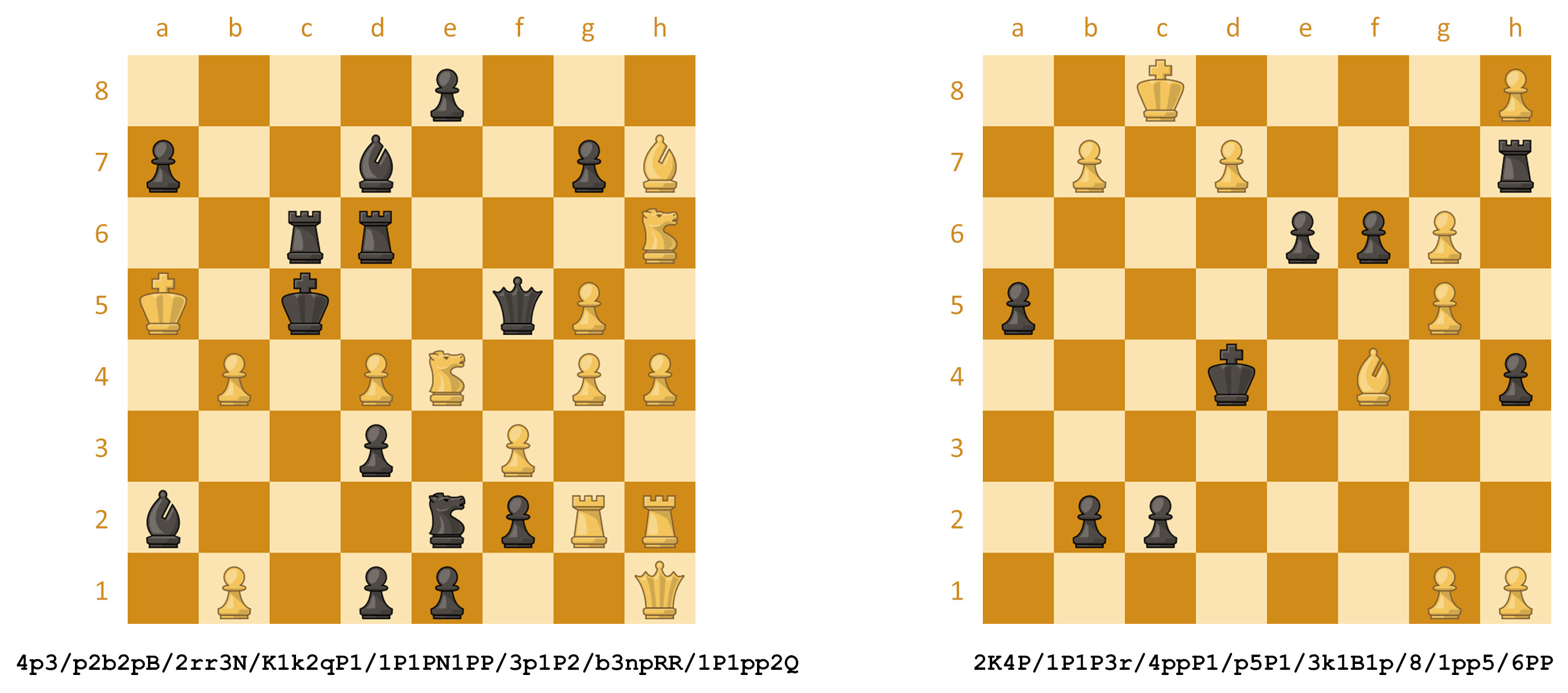
Hierbij wordt elke rij (gezien vanuit het standpunt van de witte speler) beschreven, beginnend met de achtste rij en eindigend met de eerste rij. De rijen worden gescheiden door een slash (/). Binnen elke rij wordt de inhoud van elk veld beschreven van de a-lijn tot de h-lijn. Witte stukken worden aangegeven met hun Engelse aanduiding in hoofdletters (KQRBNP), zwarte stukken met diezelfde aanduiding in kleine letters (kqrbnp). Het aantal opeenvolgende lege velden op een rij wordt aangegeven met een cijfer dat van 1 tot en met 8 kan lopen. Hieronder zie je nog twee voorbeelden van speelstukken op een schaakbord met bijhorende omschrijving in FEN-notatie.

Opgave

Elke regel van het tekstbestand FEN.txt¹ bestaat uit een patroon $$p \in \mathcal{P}$$, gevolgd door een spatie en een woord $$w \in \mathcal{W}$$. De verzameling $$\mathcal{P}$$ bevat de FEN-notaties van alle mogelijke manieren waarop een deel van de speelstukken op een schaakbord kunnen geplaatst worden. De verzameling $$\mathcal{W}$$ bevat alle woorden die enkel bestaan uit letters. Gevraagd wordt:

1. Bepaal zo kort mogelijke reguliere expressies voor de volgende deelverzamelingen van $$\mathcal{P}$$:

   • $$\mathcal{P}_1 = \{\,p \in \mathcal{P}\,|\,$$er staan 8, 9, 10, 11 of 12 pionnen op het schaakbord$$\,\}$$

     voorbeeld:	1p3qp1/R2P2Pp/2n5/1pP5/kbP2p2/1P4B1/5K2/2B1Q2N $$\in \mathcal{P}_1$$
     	7R/1p6/2b1B1P1/3npp2/1pn5/Q3PP2/1r5K/4q1R1 $$\not \in \mathcal{P}_1$$

   • $$\mathcal{P}_2 = \{\,p \in \mathcal{P}\,|\,$$er staat minstens één pion op elke rij van het schaakbord$$\,\}$$

     voorbeeld:	ppQp1K2/2Pb4/3k2nP/5P2/1p5B/P3P1NR/2p1PpNP/7p $$\in \mathcal{P}_2$$
     	6pP/3p2P1/rP1n4/8/2Bp1P1b/8/3P1n2/K3Nr2 $$\not \in \mathcal{P}_2$$

   • $$\mathcal{P}_3 = \{\,p \in \mathcal{P}\,|\,$$op het schaakbord staan geen twee speelstukken van dezelfde soort maar met een verschillende kleur naast elkaar op dezelfde rij$$\,\}$$

     voorbeeld:	r1b2pp1/pq1r3R/8/P1b5/3p3Q/p1Pn4/PNN2R1p/1PB2P2 $$\in \mathcal{P}_3$$
     	1K5p/7P/3p3P/1P1p3p/5R1P/1np3p1/1k1Rr1B1/5Q2 $$\not \in \mathcal{P}_3$$

   • $$\mathcal{P}_4 = \{\,p \in \mathcal{P}\,|\,$$er staat een zwart paard op de buitenste rand van het schaakbord$$\,\}$$

     voorbeeld:	1P2P2B/6pn/1PP2bqp/1r5p/r2pPP1p/1R1NP3/3B4/Nn4p1 $$\in \mathcal{P}_4$$
     	QR4p1/1Pp5/3p2B1/N1n4b/2p2Nr1/1n5P/1P3B2/3p2RK $$\not \in \mathcal{P}_4$$

   Geef telkens een Unix commando waarin de reguliere expressie gebruikt wordt door een commando uit de grep familie om enkel de regels van het tekstbestand naar stdout te schrijven waarvan het patroon $$p$$ behoort tot $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$.

2. Bepaal als volgt de woorden $$w_1\ w_2\ w_3\ w_4$$ van een geheime boodschap:

   • het woord $$w_1$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_1 \cap \mathcal{P_2}$$

   • het woord $$w_2$$ staat op de unieke regel waarvan $$p$$ behoort tot $$ \mathcal{P}_2 \cap \mathcal{P_3}$$

   • het woord $$w_3$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_3  \cap \mathcal{P_4}$$

   • het woord $$w_4$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_4 \cap \mathcal{P_1}$$

   Geef telkens een Unix commando waarin de reguliere expressies voor de verzamelingen $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$ gebruikt worden door commando's uit de grep familie om het woord $$w_j\ (j = 1, 2, 3, 4)$$ op te zoeken in het tekstbestand en uit te schrijven naar stdout. Hierbij is het niet toegelaten om het woord $$w_j$$ letterlijk uit te schrijven (bv. echo $$w_j$$).