In 2012 schreef The Royal Society onder de titel Shut down or restart?1 een vernietigend rapport over de manier waarop het onderwijs in het Verenigd Koninkrijk van de 21ste eeuw vaardigheden in computerwetenschappen (computer science) nog steeds stiefmoederlijk bleef behandelen. De Britse politiek had massaal oor voor de grote tekortkomingen, en nam de radicale beslissing om computervaardigheden vanaf september 2015 een integraal onderdeel te laten uitmaken van de leerplannen voor het lager en middelbaar onderwijs. Het gevolg is dat alle Engelse kinderen sindsdien leren programmeren vanaf de leeftijd van 5 jaar.
In het kader van deze programmahervorming werd heel wat educatief materiaal ontwikkeld om kinderen de wondere wereld van de informatica te leren ontdekken. Zo is er het initiatief CS unplugged2 — computeren zonder computers — dat lesmateriaal ontwikkelt om probleemoplossend denken te stimuleren door enkel met potlood en papier puzzels op te lossen, of met stoepkrijt op de speelplaats.

Deze opgave is geïnspireerd op een activiteit die kinderen leert hoe computers fouten in gegevens kunnen opsporen3. Als gegevens worden opgeslagen op een harde schijf of worden verstuurd van een computer naar een andere, dan gaan we er doorgaans van uit dat er tijdens dat proces niets aan de gegevens gewijzigd wordt. Maar soms gaat het mis en treden er toch ongewenste wijzigingen op in de gegevens. In deze activiteit leren de kinderen hoe ze kunnen ontdekken of er fouten in de gegevens zijn geslopen, en hoe die kunnen gecorrigeerd worden. Voor de activiteit heb je niets anders nodig dan een complete set van 52 speelkaarten. Het verloop van de activiteit gaat als volgt:
-
Vraag een kind om de speelkaarten in een rechthoekig $$r \times k$$ rooster te leggen, met $$r$$ rijen en $$k$$ kolommen. Hierbij mogen de speelkaarten willekeurig met de beeldzijde naar boven of naar onder gelegd worden.
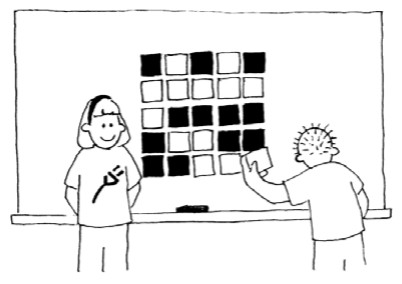
Stap 1: Leg speelkaarten willekeurig met de beeldzijde naar boven of naar onder in een rechthoekig rooster. -
Voeg zelf nog een extra rij en een extra kolom toe met de resterende speelkaarten, "om het nog een beetje moeilijker te maken". Deze kaarten vormen de sleutel tot de truc. Je moet de kaarten immers zo leggen dat er op elke rij en op elke kolom een even aantal kaarten met de beeldzijde naar boven liggen.
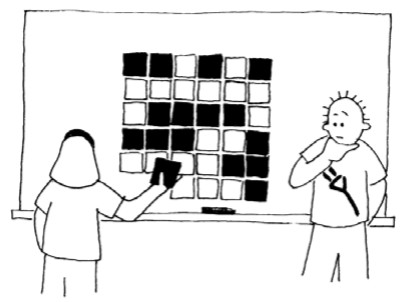
Stap 2: Vul het rooster aan met een extra rij en een extra kolom, zodat er op elke rij en op elke kolom een even aantal kaarten met de beeldzijde naar boven liggen. -
Vraag een ander kind om één van de speelkaarten om te draaien, terwijl je je ogen afdekt. De rij en de kolom die de omgedraaide speelkaart bevatten zullen nu een oneven aantal kaarten hebben die met de beeldzijde naar boven liggen, waardoor je zonder problemen de omgedraaide kaart kunt aanduiden.
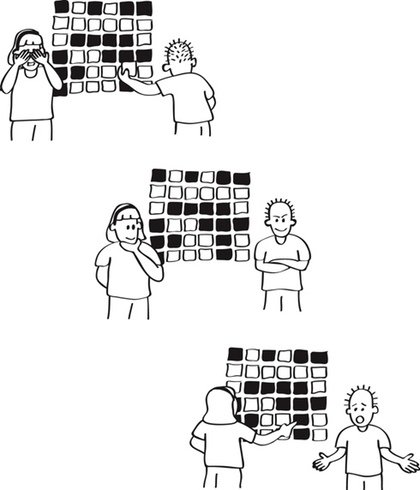
Stap 3: Draai een willekeurige kaart om, waardoor er op die rij en kolom nu een oneven aantal kaarten met de beeldzijde naar boven liggen. -
Vraag alle kinderen om te raden hoe de truc werkt. Werkt de truc ook nog als je twee of meer kaarten zou omdraaien in het rooster?
Opgave
Een complete set speelkaarten bestaat uit 52 kaarten die onderverdeeld worden in vier kleuren van elk 13 kaarten: 13 schoppen (♠), 13 harten (♥), 13 klaveren (♣) en 13 ruiten (♦). Van elke kleur zijn er telkens kaarten met een waarde van 2 tot en met 10, een boer, een vrouw, een heer en een aas. In deze opgave stellen we een speelkaart voor als een string van twee karakters. Het eerste karakter stelt de waarde van de speelkaart voor, met als mogelijke waarden de cijfers 2 tot en met 9 en de hoofdletters X (tien), J (boer, Engels: jack), Q (vrouw, Engels: queen), K (heer, Engels: king) en A (aas, Engels: ace). Het tweede karakter stelt de kleur van de speelkaart voor: S (schoppen, Engels: spades), H (harten, Engels: hearts), C (klaveren, Engels: clubs) of D (ruiten, Engels: diamonds). Zo stelt de string AS bijvoorbeeld schoppenaas voor.
In deze opgave vragen we je om vier functies te implementeren, die kunnen gebruikt worden om kaarten uit een complete set speelkaarten in een rechthoekig rooster te leggen, het rooster uit te breiden met een extra rij en een extra kolom, en een willekeurige kaart in het rooster te selecteren. Hierbij wordt een rechthoekig rooster van speelkaarten voorgesteld als een lijst van rijen speelkaarten opgelijst van boven naar onder, waarbij een rij speelkaarten zelf wordt voorgesteld als een lijst van speelkaarten opgelijst van links naar rechts. Alle speelkaarten in een rooster komen uit een complete set speelkaarten, waardoor eenzelfde speelkaart hoogstens één keer in het rooster kan voorkomen. Gevraagd wordt:
-
Schrijf een functie trekken die een willekeurige speelkaart uit een complete set speelkaarten teruggeeft, waarbij er moet voor gezorgd worden dat elke speelkaart uit de complete set evenveel kans maakt om getrokken te worden. De functie heeft een optionele parameter getrokken waaraan een container (een lijst, een tuple of een verzameling) van speelkaarten kan doorgegeven worden, die de speelkaarten voorstelt die reeds getrokken werden. Indien er een waarde aan de parameter getrokken wordt doorgegeven, dan mag de speelkaart die door de functie trekken wordt teruggegeven nooit tot de gegeven container van speelkaarten behoren.
-
Schrijf een functie leggen met twee optionele parameters rijen en kolommen (standaardwaarde is voor beide parameters gelijk aan 5). De functie moet een rechthoekig rooster van speelkaarten teruggeven, met het opgegeven aantal rijen en kolommen. De kaarten die in het rooster gelegd worden, moeten willekeurig getrokken worden uit een complete set speelkaarten. Daarbij geldt dat eenzelfde speelkaart hoogstens één keer kan getrokken worden. Het rooster moet minstens één rij en één kolom hebben, en kan uiteraard niet meer dan 52 kaarten bevatten. Indien dit niet het geval zou zijn, dan moet de functie een AssertionError opwerpen met de boodschap ongeldig rooster.
-
Schrijf een functie aanvullen waaraan een rechthoekig rooster van speelkaarten moet doorgegeven worden. De functie moet het gegeven rooster van speelkaarten uitbreiden door rechts een extra kolom van speelkaarten en onderaan een extra rij van speelkaarten toe te voegen. De speelkaarten waarmee het rooster wordt aangevuld, komen uit dezelfde complete set speelkaarten waarmee het gegeven rooster gevormd werd. Indien het gegeven rooster onmogelijk kan aangevuld worden met een extra rij en een extra kolom, omdat er niet voldoende speelkaarten in een complete set zitten, dan moet de functie een AssertionError opwerpen met de boodschap ongeldig rooster.
-
Schrijf een functie aanduiden waaraan een rechthoekig rooster van speelkaarten moet doorgegeven worden. De functie moet de positie van een willekeurige speelkaart in het rooster teruggeven. Hierbij wordt de positie van een speelkaart voorgesteld als een tuple met twee natuurlijke getallen die respectievelijk de rij- en kolomindex van de speelkaart in het rooster aangeven. De rijen worden van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf nul. Zorg ervoor dat elke speelkaart in het rooster evenveel kans maakt om aangeduid te worden.
Voorbeeld
>>> trekken()
'6S'
>>> trekken(['6H', '3C', '3D', '8C', 'AD', '9D', '7D', 'QC'])
'4D'
>>> trekken(getrokken=('3S', '8H', '8C', '2H', 'AC'))
'XH'
>>> trekken({'4C', 'AH', 'JS', '7S', '9H', '2H', 'QC', '2S', '3H', '7C'})
'9S'
>>> leggen(rijen=3, kolommen=4)
[['5D', '4D', '4C', '9S'], ['2D', '6C', '4S', 'AD'], ['QH', 'QS', '2S', '3D']]
>>> leggen(rijen=7, kolommen=8)
Traceback (most recent call last):
AssertionError: ongeldig rooster
>>> rooster = [['QH', '9S', '3C'], ['5D', '8C', '2H']]
>>> aanvullen(rooster)
>>> rooster
[['QH', '9S', '3C', 'JH'], ['5D', '8C', '2H', '9H'], ['XD', 'XC', '4C', '9C']]
>>> rooster = [['RA', 'K6', 'RV', 'H7'], ['R6', 'KX', 'KX', 'KV'], ['R8', 'R4', 'R7', 'K3']]
>>> aanduiden(rooster)
(1, 3)