In de wereldzeeën kom je nooit verder van het vasteland dan in Point Nemo voordat je je terug dichter bij land begint te begeven. Point Nemo ligt op exact 2688.22 kilometer (of 1450 zeemijlen) van de dichtste landmassa en er bestaat geen enkel ander punt in de oceaan dat zo ver van land verwijderd is. Het werd vernoemd naar het fictieve personage kapitein Nemo dat de hoofdrol speelt in Jules Vernes roman Twintigduizend mijlen onder zee (1870).
Op een planeet zoals de onze met haar complexe landmassa's en oceanen die bezaaid liggen met duizenden eilanden — waarvan sommige niet groter dan een voetbalveld — is het vinden van het meest geïsoleerde punt in de oceanen geen sinecure. Uit de meetkunde weten we bovendien dat een dergelijk punt niet altijd verst van één maar van drie kustlijnen moet verwijderd zijn, als het wil voldoen aan de voorwaarde dat het verst van elke landmassa verwijderd is. Gelukkig beschikken we vandaag de dag over computers met voldoende rekenkracht om de zoektocht naar dit punt te vergemakkelijken.
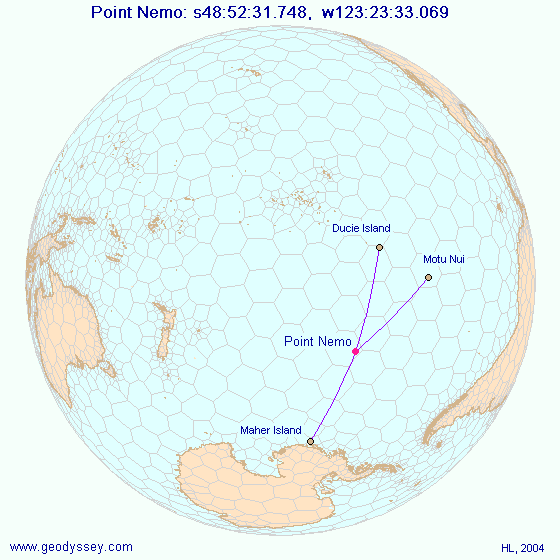
Met geografische coördinaten 48°52.6'Z 123°23.6'W ligt Point Nemo 2688.22 kilometer verwijderd van de volgende drie kustlijnen:
-
Ducie-eiland
-
Motu Nui
-
Maher-eiland
Ducie-eiland is een klein onbewoond C-vormig landstrookje met een diameter van nauwelijks twee kilometer. Motu Nui is ook een klein stukje land (nauwelijks 100 meter in doorsnede), maar het ligt in de buurt van een bekender groter eiland: Rapa Nui of beter bekend als Paaseiland. Het is op Rapa Nui dat je honderden Moai kunt zien — monolithische beelden die gehouwen werden uit vulkanisch gesteente. Het 20 kilometer brede vulkanische eiland Rapa Nui heeft zijn eigen luchthaven en ontwikkelde zich tot een toeristische bestemming. Het derde, Maher-eiland, is een klein hoefvormig eiland nabij het grotere Siple-eiland in de Zuidelijke Oceaan nabij de kustlijn van Marie Byrdland op Antartica.

Als je je echt heel erg eenzaam begint te voelen in de buurt van Point Nemo en beslist om terug te keren, dan is je beste optie om richting noordoosten te varen tot aan Paaseiland (een slordige 2688 kilometer van je vandaan), even te genieten van de historische Moai en daarna het eerste het beste vliegtuig huiswaarts te nemen.
Opgave
In deze opgave werken we met landkaarten die in een tekstbestand worden opgeslagen. De omschrijving van een kaart bestaat uit een aantal regels die allemaal even lang zijn. Elke regel bestaat enkel uit hekjes (#) die stukken land voorstellen en spaties die stukken oceaan voorstellen. Elke kaart heeft minstens één stuk land en minstens één stuk oceaan. Hieronder zie je een voorbeeld van een kaart die bestaat uit 25 regels die elk 80 karakters bevatten.
## ##### ##### # ####
## #### ########## ####
# #### ############ ##
##### ##################
##### ########### ###
##### # ######
###
##### ###
######## #######
##################
### ##################
#### ### #################
##### ##### ### #################
############ ##### ###########
########### ### ###### ########
######### ####### ####### ######
##### ####### ##### ###
## ####### ###
## ####### # #
#### ####### ## #
##### ###### #### ### #
###### ####### ########### #### # #
###### ###### ########### ##### ### #
###### ### ####### ########## #### ###
##### #### ####### #### #####
Een punt op de kaart wordt omschreven aan de hand van een tuple $$(r, k)$$ waarbij $$r$$ aangeeft op welke regel het punt gelegen is en $$k$$ aangeeft met welk karakter op die regel het punt correspondeert. Hierbij worden de regels van boven naar onder genummerd vanaf 0, en worden de karakters op een regel van links naar rechts genummerd vanaf 0. Het punt $$(0, 0)$$ ligt dus in de linkerbovenhoek van de kaart.
Om de afstand $$d_M$$ tussen twee punten $$(r_1, k_1)$$ en $$(r_2, k_2)$$ te bepalen, maken we in deze opgave geen gebruik van de Euclische afstand (vogelvlucht), maar van de Manhattan-afstand. Deze laatste wordt gedefinieerd als de som van de absolute verschillen tussen de coördinaten van de twee punten: \[ d_M((r_1, k_1), (r_2, k_2)) = |r_1 - r_2| + |k_1 - k_2|\] De naam verwijst naar de roostervormige opzet van de meeste lanen en straten op het eiland Manhattan, zoals vastgelegd in een plan uit 1811. Dit rooster zorgt ervoor dat de kortste route die een voetganger of auto kan nemen om de afstand tussen twee punten in de stad te overbruggen, een lengte heeft die gelijk is aan de afstand tussen twee punten in de Manhattan-afstand (zie onderstaande afbeelding voor een voorbeeld).
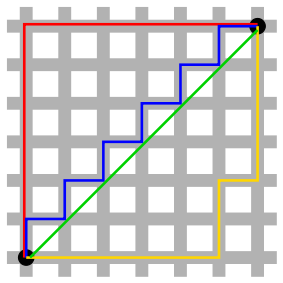
Je opdracht bestaat erin om alle punten op een gegeven kaart te bepalen met de grootste Manhattan-afstand tot de dichtste landmassa. Hiervoor definieer je een klasse Kaart die minstens ondersteuning moet bieden voor de volgende methoden:
-
Een initialisatiemethode waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit bestand moet de omschrijving van een landkaart bevatten in het formaat zoals hierboven omschreven.
-
Een methode isolement waaraan twee integers $$r$$ en $$k$$ moeten doorgegeven worden die de coördinaten $$(r, k)$$ van een punt op de kaart voorstellen. De methode moet de Manhattan-afstand van het punt $$(r, k)$$ tot de dichtste landmassa teruggeven.
-
Een methode nemo waaraan geen argumenten moeten doorgegeven worden. De methode moet een verzameling teruggeven met alle punten op de kaart waarvoor de Manhattan-afstand tot de dichtste landmassa het grootst is.
-
Een methode __str__ die een stringvoorstelling van de kaart teruggeeft. Deze stringvoorstelling moet dezelfde vorm hebben als de oorspronkelijke voorstelling van de kaart in het gegeven tekstbestand, maar waarbij alle punten op de kaart waarvoor de Manhattan-afstand tot de dichtste landmassa het grootst is worden voorgesteld door de hoofdletter X.
Opmerking: Los van het feit dat de Aarde bolvormig is, hoef je de gegeven landkaarten niet te zien als een vlakke projectie van een bol. Bij het bepalen van de afstanden hoef je dus GEEN rekening te houden met het feit dat de rechterkant moet aansluiten op de linkerkant, of dat de onderkant moet aansluiten op de bovenkant.
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat het bestand kaart.txt zich in de huidige directory bevindt.
>>> kaart = Kaart('kaart.txt')
>>> kaart.isolement(0, 0)
1
>>> kaart.isolement(1, 2)
0
>>> kaart.isolement(2, 3)
2
>>> kaart.isolement(7, 78)
12
>>> kaart.isolement(11, 74)
12
>>> kaart.nemo()
{(7, 78), (11, 74), (8, 77), (10, 75), (6, 79), (9, 76)}
>>> print(kaart)
## ##### ##### # ####
## #### ########## ####
# #### ############ ##
##### ##################
##### ########### ###
##### # ######
### X
##### ### X
######## ####### X
################## X
### ################## X
#### ### ################# X
##### ##### ### #################
############ ##### ###########
########### ### ###### ########
######### ####### ####### ######
##### ####### ##### ###
## ####### ###
## ####### # #
#### ####### ## #
##### ###### #### ### #
###### ####### ########### #### # #
###### ###### ########### ##### ### #
###### ### ####### ########## #### ###
##### #### ####### #### #####
Epiloog
In juni 1928 publiceert H.P. Lovecraft het sciene fiction kortverhaal De roep van Cthulhu, waarin voor het eerst gewag gemaakt wordt van Cthulhu. Deze fictieve monsterlijke godheid die miljoenen jaren geleden op aarde terechtkwam, wordt beschreven als een kolossaal wezen dat zijn tijd doorbrengt in de verzonken stad R'lyeh die zich vlak bij Point Nemo zou bevinden.
De virtuele Britse band Gorillaz
beweert dat Point Nemo de locatie is van haar voormalige hoofdkwartier,
een drijvend eiland gemaakt van ronddobberend afval dat bekend staat als
Plastic Beach.