De bitcoin is een digitale munteenheid waarvan de waarde dagelijks sterk kan fluctueren. Van een kennis met voorspellende gaven heb je een tabel gekregen met de waarde $$v_i$$ ($$i = 1, 2, \ldots, n$$) van de bitcoin in euro's voor de komende $$n$$ dagen. Daarmee kan je uiteraard aan de slag om zoveel mogelijk winst te proberen maken door in die periode bitcoins te kopen en te verkopen. Daarbij gelden de volgende regels:

aan het begin van de periode heb je geen bitcoin
aan het einde van de periode heb je ook geen bitcoin
je mag nooit meer dan één bitcoin tegelijkertijd in je bezit hebben
elke dag van de periode kan je ofwel een bitcoin kopen als je er geen in je bezit hebt, of de bitcoin die je in bezit hebt verkopen, of helemaal niets doen (op dezelfde dag mag je dus niet én de bitcoin die je hebt verkopen én een nieuwe bitcoin kopen)

Het doel is om op het einde van de periode zoveel mogelijk winst te maken. Voor grote waarden van $$n$$ wordt het al snel onmogelijk om alle mogelijkheden voor het kopen en verkopen van bitcoins te evalueren, om te zien welk van die mogelijkheden de maximale winst oplevert. We kunnen de maximale winst echter wel op een snelle manier bepalen door gebruik te maken van een algoritmische techniek die dynamisch programmeren genoemd wordt.

Concreet berekenen we de waarden $$p_i$$ ($$i = 1, 2, \ldots, n$$) die de maximale winst uitdrukken als we op het einde van dag $$i$$ geen bitcoin hebben, en de waarden $$p'_i$$ ($$i = 1, 2, \ldots, n$$) die de maximale winst uitdrukken als we op het einde van dag $$i$$ wel een bitcoin hebben. Deze waarden worden dag per dag berekend. Voor de eerste dag geldt dat: \[ \begin{cases} p_1 = 0 \\ p'_1 = -v_1 \end{cases} \] Voor alle volgende dagen ($$i = 2, 3, \ldots, n$$) geldt dan: \[ \begin{cases} p_i = \max(p_{i - 1}, p'_{i - 1} + v_i) \\ p'_i = \max(p'_{i - 1}, p_{i - 1} - v_i) \end{cases} \] De maximale winst op het einde van de periode van $$n$$ dagen (waarbij we geen bitcoin hebben op het einde van die periode) wordt dan gegeven door $$p_n$$.

Stel bijvoorbeeld dat bitcoins in de periode van de komende $$n = 10$$ dagen achtereenvolgens €5, €11, €4, €2, €8, €10, €7, €4, €3 en €6 waard zullen zijn. Op het einde van de eerste dag kunnen we de maximale winsten berekenen als $$p_1 = 0$$ en $$p'_1 = -v_1 = -5$$.

Maximale winst op de eerste dag.

Op basis van de maximale winsten op het einde van de eerste dag, kunnen we nu ook de maximale winsten op het einde van de tweede dag berekenen als \[ p_2 = \max(p_1, p'_1 + v_2) = \max(0, -5 + 11) = 6 \] en \[ p'_2 = \max(p'_1, p_1 - v_2) = \max(-5, 0 - 11) = -5 \] We krijgen dan

Maximale winst op de tweede dag.

Op een analoge manier kunnen we nu ook dag per dag de maximale winsten bepalen voor de overige dagen van de periode.

Maximale winst op de laatste dag.

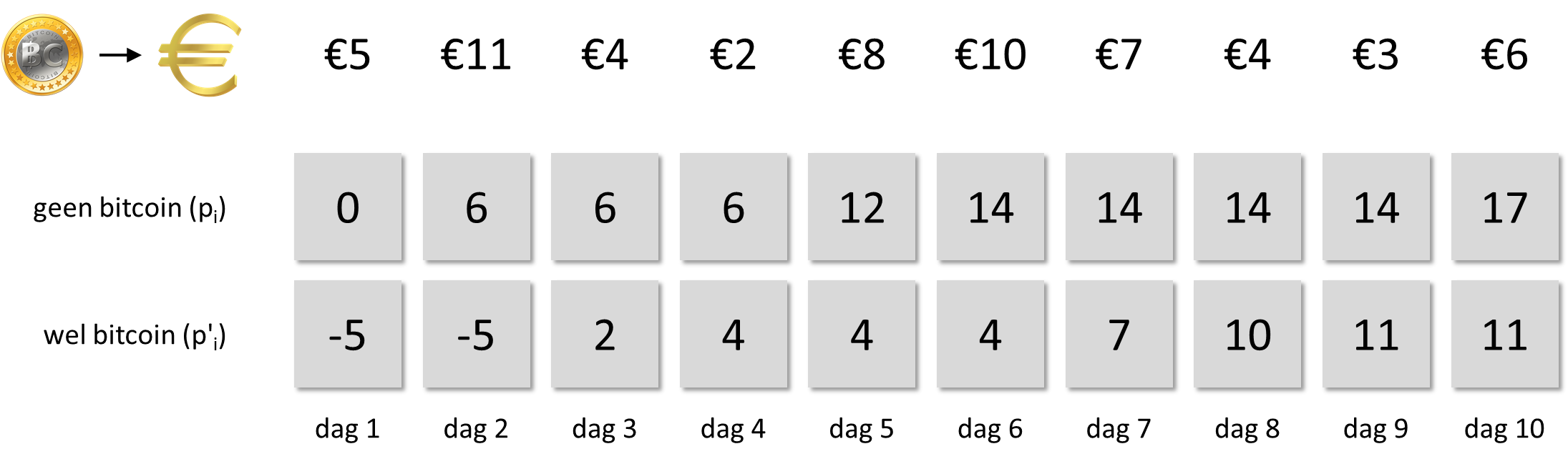
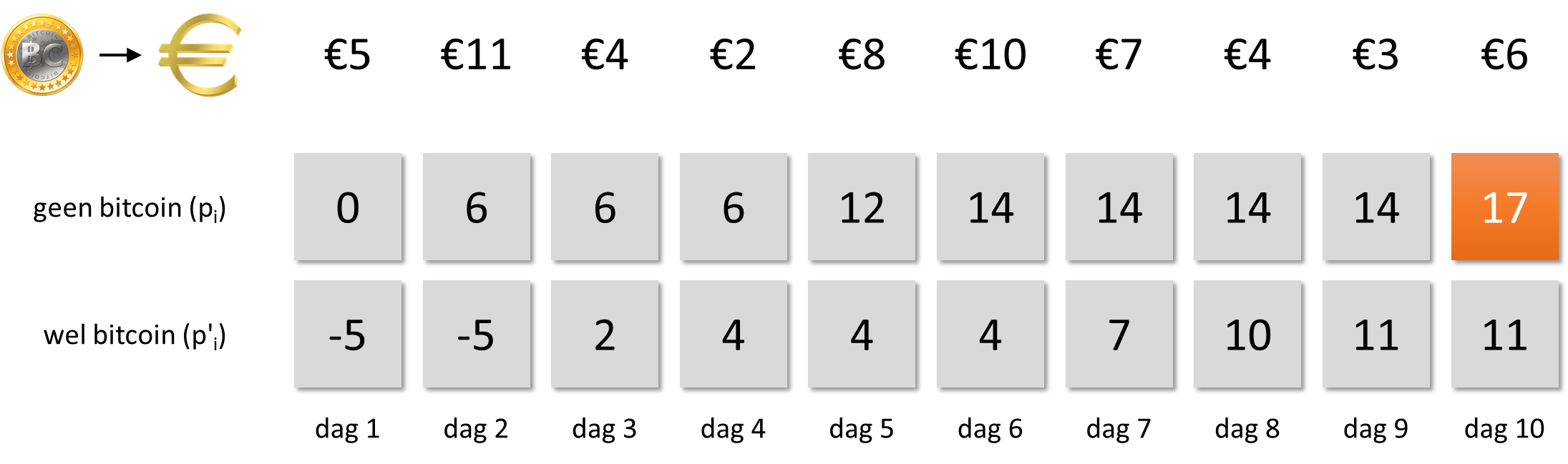
De maximale winst als we op het einde van de periode geen bitcoin in handen hebben, kunnen we nu gewoon aflezen uit de maximale winsten op de laatste dag van de periode.

Maximale winst als we op de laatste dag geen bitcoin hebben.

Opgave

We stellen de acties die we uitvoeren tijdens een periode van $$n$$ dagen waarin we bitcoins kopen en verkopen voor als een string (String) van $$n$$ karakters, waarbij enkel de volgende karakters kunnen voorkomen:

een hoofdletter K stelt voor dat we op die dag een bitcoin kopen
een hoofdletter V stelt voor dat we op die dag een bitcoin verkopen
een koppelteken (-) stelt voor dat we op die dag geen bitcoins kopen of verkopen

Uiteraard moeten deze acties voldoen aan de regels rond het kopen en verkopen van bitcoins zoals gesteld in de inleiding van deze opgave. Gevraagd wordt:

Schrijf een functie winst waaraan twee argumenten moeten doorgegeven worden: i) een array (Array) met $$n \in \mathbb{N}_0$$ integers (Number) die de waarde van de bitcoin (in euro) voorstellen doorheen een periode van $$n$$ opeenvolgende dagen en ii) een string (String) die de acties omschrijft die we uitvoeren tijdens deze periode van $$n$$ dagen waarin we bitcoins kopen en verkopen. De functie moet de winst (Number) teruggeven die we bekomen als we de gegeven acties uitvoeren binnen de periode van $$n$$ dagen, met de gegeven waarde van de bitcoin tijdens die periode. Indien de gegeven acties niet voldoen aan de regels rond het kopen en verkopen van bitcoins zoals gesteld in de inleiding van deze opgave, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige acties.
Schrijf een functie maximaleWinst waaraan een array (Array) met $$n \in \mathbb{N}_0$$ integers (Number) moet doorgegeven worden. Deze integers stellen de waarde van de bitcoin (in euro) voor doorheen een periode van $$n$$ opeenvolgende dagen waarbinnen we bitcoins kunnen kopen en verkopen. De functie moet de maximale winst (Number) teruggeven die je kunt bekomen door het kopen en verkopen van bitcoins tijdens deze periode, rekening houdend met de regels die gesteld werden in de inleiding van deze opgave. Merk op dat deze winst eventueel 0 kan zijn, aangezien je überhaupt niet verplicht bent om binnen de periode ook maar één bitcoin aan te kopen.

Voorbeeld

        > winst([5, 11, 4, 2, 8, 10, 7, 4, 3, 6], "KV-K-V--KV")
17
> winst([4, 2, 5, 11, 10, 4, 11, 7, 4, 11, 3, 11], "-K-V-KV-KVKV")
31
> winst([10, 9, 9, 10, 10, 9, 1, 4, 9, 3, 5, 6, 10], "-K-V--K-VK--V")
16
> winst([12, 4, 9, 5, 6, 7, 9, 9, 11, 7, 10], "-KVK----VKV")
14
> winst([10, 9, 8, 7, 6, 5, 4, 3, 2, 1], "----------")
0
> winst([10, 4, 2, 4, 8, 12], "K---VV")
AssertionError: ongeldige acties

> maximaleWinst([5, 11, 4, 2, 8, 10, 7, 4, 3, 6])
17
> maximaleWinst([4, 2, 5, 11, 10, 4, 11, 7, 4, 11, 3, 11])
31
> maximaleWinst([10, 9, 9, 10, 10, 9, 1, 4, 9, 3, 5, 6, 10])
16
> maximaleWinst([12, 4, 9, 5, 6, 7, 9, 9, 11, 7, 10])
14
> maximaleWinst([10, 9, 8, 7, 6, 5, 4, 3, 2, 1])
0
> maximaleWinst([10, 4, 2, 4, 8, 12])
10