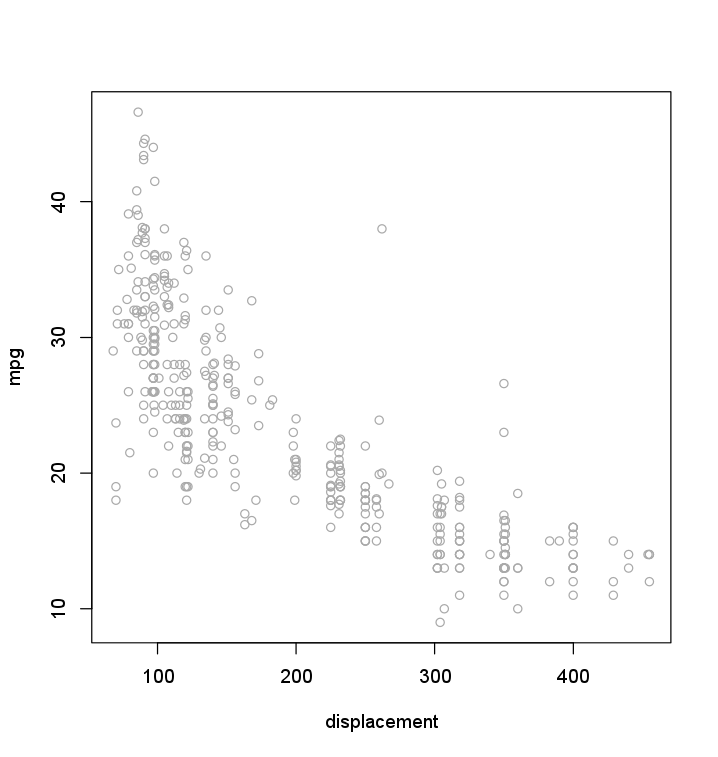
In this exercise, we use the Auto data set. There seems to be a nice non-linear relationships between displacement (the cylinder volume) and the dependent variable mpg. We fit a series of non-linear models to investigate the relationship.

Questions

Some of the exercises are not tested by Dodona (for example the plots), but it is still useful to try them.

1. Fit step functions for a range of different number of cuts (from 2 to 10), and perform 10-fold cross-validation to select the optimal number of cuts.
   1. Set a seed of 1. Write a for loop of 10 iterations. In each iteration i, fit a step function of displacement to predict mpg with i cuts.
   2. Store the CV error in the i-th element of the vector deltas.cut.

      Initialize the vector deltas.cut as a vector of length 10 with values NA.

   3. Plot the CV errors for the varying number of cuts.
   4. What is the optimal number of cuts? Store the answer in d.min.cut.
      
      
2. Fit natural splines for a range of different degrees of freedom (from 3 to 10), and perform 10-fold cross-validation to select the degrees of freedom.
   1. Set a seed of 1. Write a for loop of 10 iterations. In each iteration i, fit a natural spline of displacement to predict mpg with i degrees of freedom.
   2. Store the CV error in the i-th element of the vector deltas.ns.

      Initialize the vector deltas.ns as a vector of length 10 with values NA.

   3. Plot the CV errors for the varying degrees of freedom.
   4. What is the optimal degrees of freedom? Store the answer in df.min.ns.
      
      

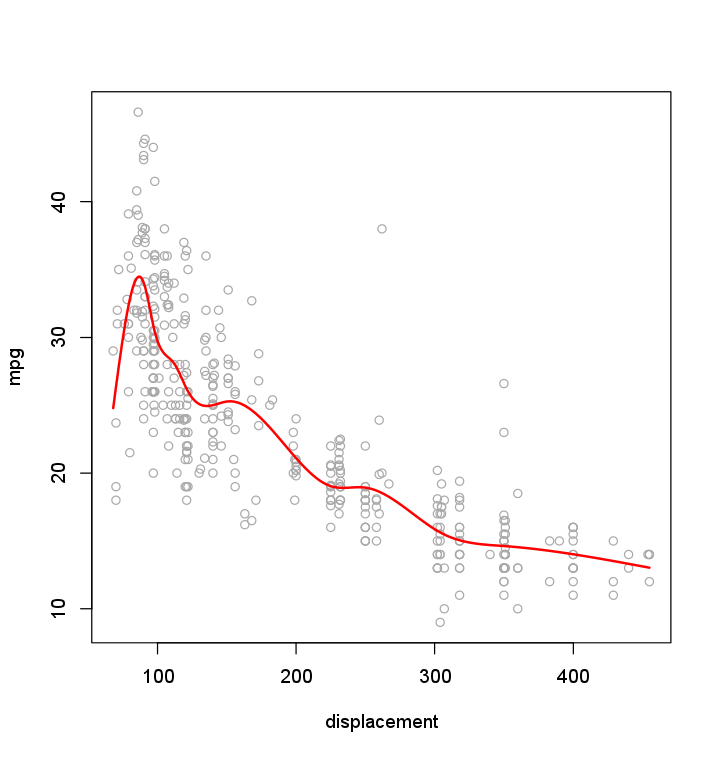
   Try to fit the best natural spline model on the plot above:

   1. Create a scatterplot of mpg vs displacement using all the data.
   2. Create a sequence displacement.grid of values ranging from the lowest displacement value in the data to the highest displacement value observed, in steps of 0.1.
   3. Create the model fit.ns using the optimal degrees of freedom df.min.ns,
   4. predict mpg for the entire sequence. Store the result in preds.
   5. Add the predictions preds on the plot.

---

Assume that:

• The ISLR2 library has been loaded
• The Auto dataset has been loaded and attached
• The boot library has been loaded
• The splines library has been loaded