Bacteriorhodopsine is een 7-transmembraan eiwit, wat betekent dat het is opgebouwd uit zeven helices die het celmembraan doorkruisen (zie onderstaande figuur, links). Als gevolg hiervan moet dit eiwit bestaan uit zeven hydrofobe (waterafstotende) segmenten die niet reageren met het vette celmembraan, afgewisseld met hydrofiele segmenten die niet reageren met het waterige cytoplasma en de omgeving buiten de cel. Aan elk aminozuur van een eiwit kan een gradatie van hydrofobiciteit toegekend worden, gaande van zeer hydrofoob naar zeer hydrofiel. Onderstaande tabel (rechts) geeft de hydrofobiciteitswaarden voor de verschillende aminozuren (positieve waarden zijn hydrofoob en negatieve waarden zijn hydrofiel) zoals die werden bepaald door Kyte en Doolittle1.
| residu | waarde |
|---|---|
| A | 1.8 |
| R | -4.5 |
| N | -3.5 |
| D | -3.5 |
| C | 2.5 |
| Q | -3.5 |
| E | -3.5 |
| G | -0.4 |
| H | -3.2 |
| I | 4.5 |
| residu | waarde |
|---|---|
| L | 3.8 |
| K | -3.9 |
| M | 1.9 |
| F | 2.8 |
| P | -1.6 |
| S | -0.8 |
| T | -0.7 |
| W | -0.9 |
| Y | -1.3 |
| V | 4.2 |
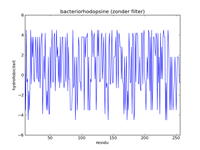
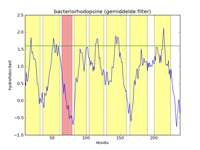
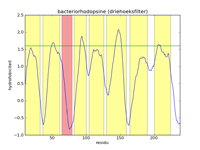
De linker figuur hieronder geeft een afbeelding van de lijst met datapunten die de hydrofobiciteitswaarden van bacteriorhodopsine voorstellen. Een hydrofobiciteitswaarde geeft de kans aan dat een bepaald aminozuur in een hydrofobe regio voorkomt. Het is echter geen exacte voorspelling. Een aminozuur met een hoge hydrofobiciteit kan nog steeds in water voorkomen, en omgekeerd. Hierdoor bevat het signaal heel veel ruis, en is het vrijwel onmogelijk om hydrofobe regio's te vinden in deze figuur. Door toepassing van een wiskundige filtertechniek kan de ruis onderdrukt worden. In de middelste figuur werd bijvoorbeeld gebruikgemaakt van een gemiddelde filter, en worden de zeven helices aangegeven als gele stroken. Hierin zien we duidelijk dat de filtering het signaal versterkt, en kunnen de pieken van hoge hydrofobiciteit duidelijk gelinkt worden aan de regio's waar de helices zich bevinden. De rechter figuur is analoog aan de middelste figuur, maar maakt gebruik van een driehoeksfilter. Het effect is dat het signaal nog verder versterkt wordt.
Opgave
Schrijf een functie hydrofobiciteit waaraan twee verplichte argumenten moeten doorgegeven worden: een eiwitsequentie (string bestaande uit letters die aminozuren voorstellen) en een dictionary die elk aminozuur afbeeldt op een corresponderende hydrofobiciteitswaarde. De functie moet als resultaat een lijst teruggeven met de hydrofobiciteitswaarden van de opeenvolgende aminozuren van de eiwitsequentie.
Stel dat we beschikken over een lijst van datapunten die we voorstellen als $$x_0, x_1, \ldots, x_n$$. Een filter bestaat uit een lijst van gewichten $$w_0, w_1, \ldots, w_m$$ (met $$m$$ even en $$m \leq n$$). Door de filter toe te passen op de lijst van datapunten bekomen we een nieuwe (afgevlakte) lijst van datapunten $$y_0, y_1, \ldots y_{n-m}$$, waarvan de waarden op de volgende manier berekend worden.
\[ y_i = \frac{\displaystyle\sum_{j=0}^m w_j x_{i+j}}{\displaystyle\sum_{j=0}^m w_j},\ 0 \leq i \leq n-m \]Schrijf een functie filter waaraan twee argumenten moeten doorgegeven worden: een lijst van datapunten en een lijst van gewichten. De datapunten en gewichten zijn reële getallen. De functie moet de afgevlakte lijst van datapunten teruggeven die resulteert na toepassing van de filter op de oorspronkelijke lijst van datapunten.Als alle gewichten van de filter eenzelfde waarde $$w$$ ($$w \neq 0$$) hebben, dan berekent de filter het gemiddelde van de waarde van een datapunt en een aantal naburige punten links en rechts van dit punt. Als we bijvoorbeeld de lijst [1, 1, 1, 1, 1] als filter gebruiken, dan worden 5 punten uitgemiddeld (een punt en twee punten links en rechts). We noemen dit een gemiddelde filter met breedte $$b = 5$$. Analoog gebruikt een gemiddelde filter met breedte $$b = 7$$ als filter de lijst [1, 1, 1, 1, 1, 1, 1]. Gebruik de functie filter om een functie filterGemiddelde te schrijven waaraan verplicht een lijst van datapunten (argument datapunten) en optioneel een breedte $$b$$ (argument breedte; gebruik $$b=5$$ als standaardwaarde) moeten doorgegeven worden. Deze functie moet als resultaat de afgevlakte lijst van datapunten teruggeven die resulteert na toepassing van een gemiddelde filter met breedte $$b$$. Indien de opgegeven breedte $$b$$ even is, dan moet de functie die met 1 verhogen (de breedte moet immers altijd oneven zijn).
Een driehoeksfilter maakt gebruik van een filter die in het eerste deel oploopt vanaf 1, en halverwege terug begint af te lopen. Zo maakt een driehoeksfilter met breedte $$b=5$$ gebruik van de filter [1, 2, 3, 2, 1], een driehoeksfilter met breedte $$b=7$$ van de filter [1, 2, 3, 4, 3, 2, 1], enzoverder. Gebruik de functie filter om een functie filterDriehoek te schrijven waaraan verplicht een lijst van datapunten (argument datapunten) en optioneel een breedte $$b$$ (argument breedte; gebruik $$b=5$$ als standaardwaarde) moeten doorgegeven worden. Deze functie moet als resultaat de afgevlakte lijst van datapunten teruggeven die resulteert na toepassing van een driehoeksfilter met breedte $$b$$. Indien de opgegeven breedte $$b$$ even is, dan moet de functie die met 1 verhogen (de breedte moet immers altijd oneven zijn).
Voorbeeld
>>> eiwit = 'AQITGRPEWI'
>>> kd = {
... 'A': 1.8, 'R':-4.5, 'N':-3.5, 'D':-3.5, 'C': 2.5,
... 'Q':-3.5, 'E':-3.5, 'G':-0.4, 'H':-3.2, 'I': 4.5,
... 'L': 3.8, 'K':-3.9, 'M': 1.9, 'F': 2.8, 'P':-1.6,
... 'S':-0.8, 'T':-0.7, 'W':-0.9, 'Y':-1.3, 'V': 4.2
... }
>>> datapunten = hydrofobiciteit(eiwit, kd)
>>> datapunten
[1.8, -3.5, 4.5, -0.7, -0.4, -4.5, -1.6, -3.5, -0.9, 4.5]
>>> filterGemiddelde(datapunten)
[0.34, -0.92, -0.54, -2.14, -2.18, -1.2]
>>> filterGemiddelde(datapunten, breedte=5)
[0.34, -0.92, -0.54, -2.14, -2.18, -1.2]
>>> filterDriehoek(datapunten, breedte=3)
[-0.175, 1.2, 0.675, -1.5, -2.75, -2.8, -2.375, -0.2]