In de sterrenkunde wordt de energiedichtheid van een zwarte straler¹ per tijdseenheid en per eenheid van golflengte bepaald door de stralingsenergieformule van Planck: \[\rho(T,\lambda) = \frac{8\pi hc}{\lambda^5}\frac{1}{e^{\frac{hc}{\lambda k T}}- 1}\] Hierbij is $$T$$ de temperatuur (uitgedrukt in Kelvin), $$\lambda$$ de golflengte (uitgedrukt in meter), $$h$$ de constante van Planck ($$6,62608 \times 10^{-34}$$ Js), $$c$$ de lichtsnelheid ($$2,99792458 \times 10^8$$ ms$$^{-1}$$), en $$k$$ de constante van Boltzmann ($$1,38066 \times 10^{-23}$$ JK$$^{-1}$$).

Hint: Controleer de uitvoer van je programma aan de hand van onderstaande figuur (bron: Wikipedia²):

De wet van Planck (gekleurde lijnen) beschrijft nauwkeurig de stralingsenergie van een zwart lichaam, met een voorstelling die zegt dat elektromagnetische straling³ uitgezonden werd door kwanta⁴. Deze wet lost met succes de ultravioletcatastrofe⁵ op — een groot probleem in de klassieke fysica — waarmee het een belangrijk resultaat neerzette voor de ontwikkeling van de kwantummechanica⁶.

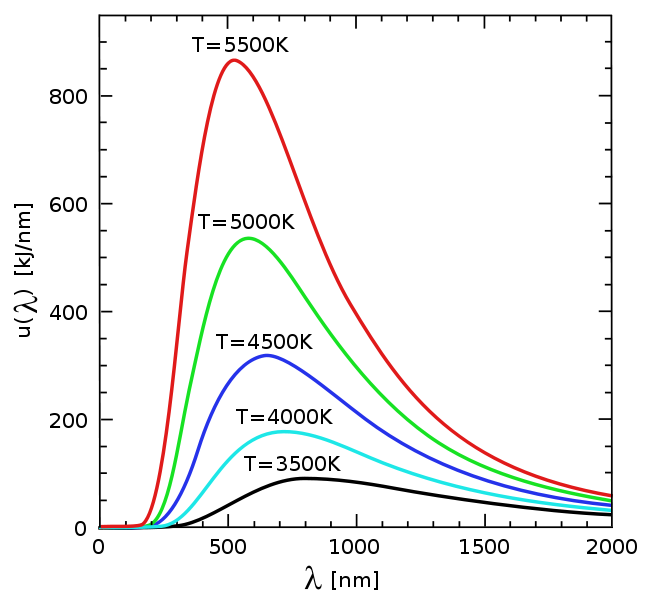
Invoer

De invoer bestaan uit $$t$$ testgevallen ($$t \leq 50$$). De eerste regel van de invoer bevat een natuurlijk getal $$t$$. Daarna volgen $$t$$ regels die de verschillende testgevallen omschrijven. Voor elk testgeval bevat de invoer twee regels. De eerste regel bevat een gegeven temperatuur $$T$$ uitgedrukt in Kelvin. De tweede regel bevat een gegeven golflengte $$\lambda$$ uitgedrukt in micrometer (1 micrometer = $$10^{-6}$$ meter).

Uitvoer

Voor elk testgeval de energiedichtheid $$\rho$$ in SI-eenheden (dit is Joule per m$$^4$$) die correspondeert met de gegeven temperatuur $$T$$ en golflengte $$\lambda$$.

Voorbeeld

Invoer:

Uitvoer:

858255.480667
267354.545955
42955.5563284
297696.258875
140690.424377