Darren zijn mannelijke bijen die geboren worden uit een onbevrucht eitje. Ze zijn een maatje groter dan de werkbijen, maar een maatje kleiner dan de koningin. Hun ogen zijn twee keer zo groot als de ogen van de werkbijen en de koningin, maar in tegenstelling tot de werkbijen kunnen darren niet steken.
Darren halen geen honing, geen stuifmeel, voeren geen larven, bouwen geen raten en laten zich het liefst van al voeren door de werkbijen. Hun bijdrage aan de kolonie is om een klein beetje te helpen bij de temperatuurregeling. Wanneer de temperatuur te laag wordt, gaan de darren en de werkbijen warmte genereren door te trillen en wanneer de temperatuur te hoog wordt, gaan de darren net als alle werkbijen met de vleugels wapperen ter ventilatie.
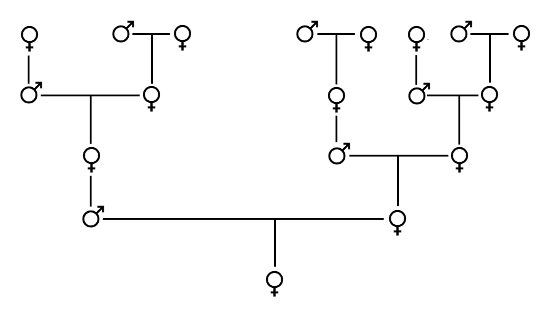
Daarnaast bestaat de enige andere taak van darren erin om te paren met de koningin. Net zoals de eitjes waaruit werkbijen en volgende generaties koninginnen geboren worden, worden eitjes waaruit de darren geboren worden, gelegd door de koningin zelf. Darren hebben dus een moeder maar geen vader, maar ze hebben wel een grootvader. Vrouwelijke bijen komen uit bevruchte eitjes en hebben dus ouders van beide geslachten. Hierdoor ontstaat een interessant patroon: het aantal darren in een bepaalde generatie is gelijk aan het aantal vrouwelijke bijen in de voorgaande generatie, en het aantal vrouwelijke bijen in een bepaalde generatie is gelijk aan het aantal vrouwelijke bijen in de voorgaande twee generaties.
| generatie | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| aantal vrouwelijke bijen | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 |
| aantal mannelijke bijen | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 |
| totaal aantal bijen | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
Het totaal aantal bijen — zowel mannelijke als vrouwelijke — in generatie $$n$$ is hierdoor dus gelijk aan het Fibonaccigetal $$F_n$$. Dit patroon werd in 1921 ontdekt door W. Hope-Jones.
Invoer
De invoer bestaat uit één getal $$n \in \mathbb{N}$$ dat het volgnummer van een generatie aangeeft. Generaties worden hierbij genummerd vanaf nul, waarbij we veronderstellen dat de eerste generatie (generatie 0) enkel bestaat uit één mannelijke bij.
Uitvoer
Er moeten drie regels uitvoer gegenereerd worden, die respectievelijk het aantal vrouwelijke bijen, het aantal mannelijke bijen en het totaal aantal bijen in generatie $$n$$ aangeven. Bekijk onderstaand voorbeeld om te zien hoe de uitvoer precies moet opgemaakt worden.
Voorbeeld
Invoer:
7Uitvoer:
aantal vrouwelijke bijen: 13
aantal mannelijke bijen: 8
totaal aantal bijen: 21