Een drakencurve vormt een herhaald patroon dat zichzelf nooit snijdt. Je krijgt een drakencurve van orde $$n$$ ($$n \geq 0$$) wanneer je een strook papier $$n$$ keer in twee vouwt, en daarna terug ontvouwt zodat de plooien rechte hoeken vormen. De naam is afgeleid van het feit dat het patroon sterke gelijkenissen vertoont met een bepaald mytisch wezen.

De instructies om een drakencurve te tekenen kunnen neergeschreven worden als een string die enkel bestaat uit de letters V, L en R. Hierbij staat de instructie V voor "teken een lijn terwijl je één stap vooruit zet", de instructie L betekent "draai 90° in tegenwijzerzin", en de instructie R betekent "draai 90° in wijzerzin". De sleutel tot het neerschrijven van de instructies komt voort uit de vaststelling dat een curve van orde $$n$$ ($$n > 0$$) gevormd wordt door een curve van orde $$n-1$$, gevolgd door de letter L en de curve van orde $$n-1$$ die wordt afgelegd in omgekeerde volgorde (string met instructies omkeren, L vervangen door R, en R vervangen door L). De curve van orde 0 bestaat eenvoudigweg uit een string met één enkele instructie: V. Onderstaande figuur toont de instructies om drakencurves van orde 0, 1, 2 en 3 te tekenen.

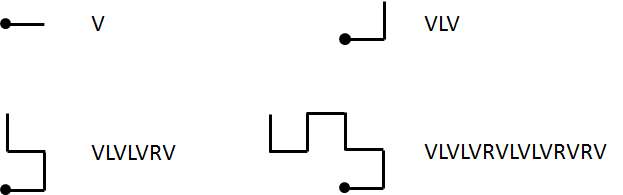
Opgave

1. Schrijf een functie drakencurve die de string met instructies teruggeeft die nodig zijn om een drakencurve van orde $$n$$ ($$n \geq 0$$) te tekenen. De orde $$n$$ moet als argument aan de functie doorgegeven worden.

2. Veronderstel een cartesisch vlak waarbij de $$x$$-as van het coördinatenstelsel naar rechts gericht is, en de $$y$$-as naar boven. Stel dat we ons initieel in de oorsprong (0,0) bevinden met onze neus in de richting van de positieve $$x$$-as. Als we nu bijvoorbeeld de instructie V van een drakencurve uitvoeren, dan komen we in het punt (1,0) terecht. Als we daarna de instructie L uitvoeren, dan staan we met onze neus richting positieve $$y$$-as. Als we nu opnieuw de instructie V uitvoeren, dan komen we in het punt (1,1) terecht.
   Schrijf een functie curve2posities waaraan een string moet doorgegeven worden die enkel bestaat uit de letters V, L en R, overeenkomstig de instructies die gebruikt worden voor het tekenen van een drakencurve. De string met instructies zelf hoeft dus niet noodzakelijk een drakencurve op te leveren. De functie moet de lijst van posities (punten in het cartesich vlak voorgesteld als tuples van lengte twee) teruggeven die achtereenvolgens bezocht worden als de instructies uit de gegeven string uitgevoerd worden.

Voorbeeld

>>> drakencurve(0)
'V'
>>> drakencurve(1)
'VLV'
>>> drakencurve(2)
'VLVLVRV'
>>> drakencurve(3)
'VLVLVRVLVLVRVRV'
>>> curve2posities('VLVLVRVLVLVRVRV')
[(0, 0), (1, 0), (1, 1), (0, 1), (0, 2), (-1, 2), (-1, 1), (-2, 1), (-2, 2)]
>>> curve2posities('VVLRLVLRLVRVVVLV')
[(0, 0), (1, 0), (2, 0), (2, 1), (1, 1), (1, 2), (1, 3), (1, 4), (0, 4)]
>>> curve2posities('LLLVRVLLVRRRVLRLV')
[(0, 0), (0, -1), (-1, -1), (0, -1), (0, 0), (-1, 0)]