Welk getal komt op de plaats van het vraagteken?

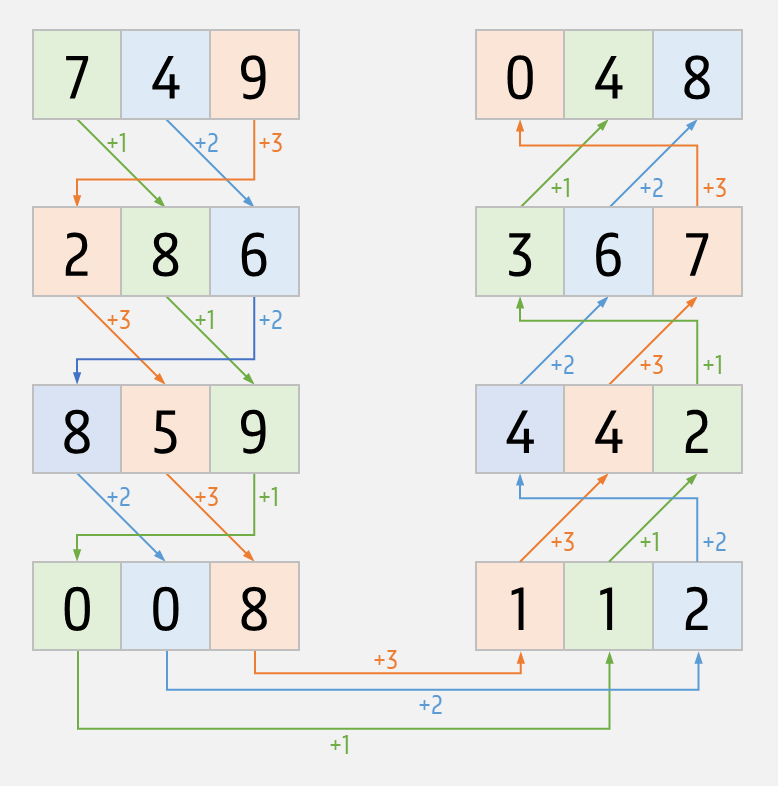
749, 286, 859, 008, 112, 442, 367, ?, …

Antwoord weergeven

Het volgende getal in de reeks is 048. Deze reeks getallen is immers een voorbeeld van een arithmetische progressie van getal 749 met verschuivingen 123.

Arithmetische progressie van 749 met verschuivingen 123.

Opgave

We stellen een getal $$d = d_1d_2\ldots d_n$$ met $$n$$ cijfers voor als een string (str).

Voor twee getallen $$d = d_1d_2\ldots d_n$$ en $$s = s_1s_2\ldots s_n$$ met $$n$$ cijfers is de arithmetische progressie van $$d$$ met verschuivingen $$s$$ een reeks getallen die begint met het getal $$d$$. Het volgende getal van de arithmetische progressie wordt telkens via een progressiestap bepaald uit het vorige getal van de reeks.

In de eerste progressiestap van de arithmetische progressie van 749 met verschuivingen 123 (rechts) verschuiven we eerst 749 met verschuivingen 123 om zo het getal 862 te bekomen (links). Daarna rollen we het getal 862 naar rechts, om zo het getal 286 te bekomen. Dit laatste getal is het resultaat van de progressiestap, en dus het tweede getal van de arithmetische progressie. Om het volgende getal van de arithmetische progressie te bepalen, gebruiken we bij de volgende progressiestap verschuivingen 312.

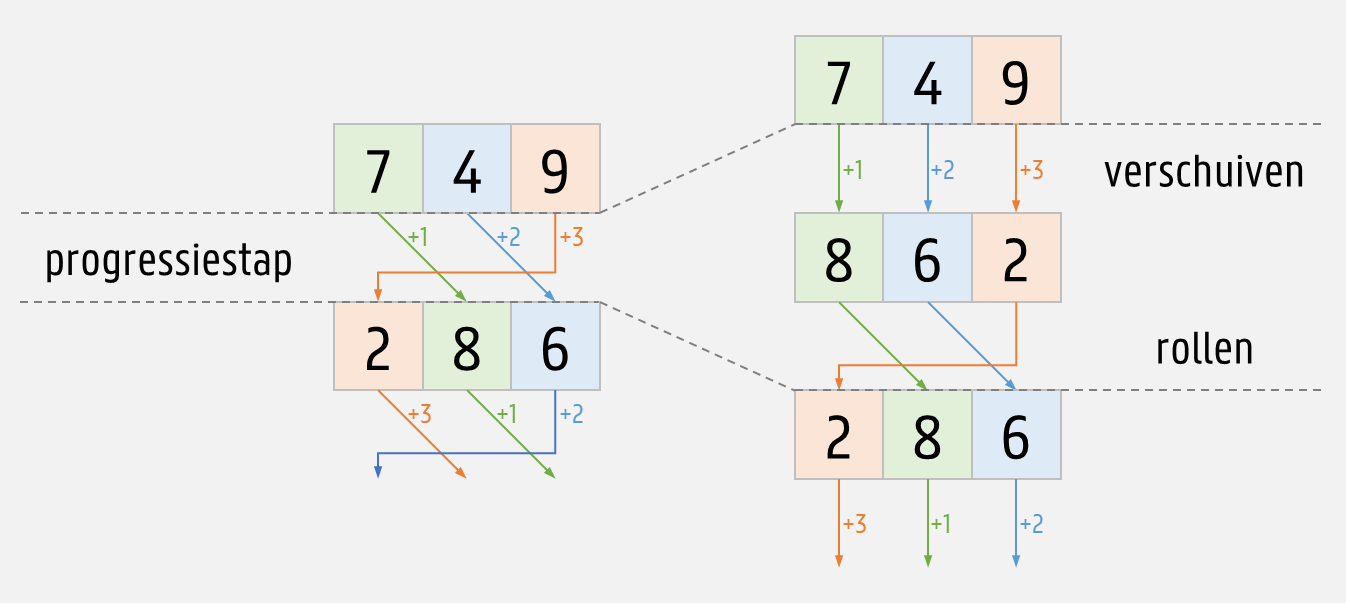
Bij een progressiestap verschuiven we eerste de cijfers van getal $$d = d_1d_2\ldots d_n$$ met verschuivingen $$s = s_1s_2\ldots s_n$$. Dit levert een nieuw getal $$d' = d'_1d'_2\ldots d'_n$$ van $$n$$ cijfers op, waarbij $$d'_i = (d_i + s_i)\!\!\!\!\mod{10}$$ voor $$i = 1, 2, \ldots, n$$ en waarbij $$\text{mod}$$ de bewerking is die de rest na deling bepaalt. Daarna rollen we het getal $$d'$$ naar rechts door alle cijfers één positie naar rechts te verplaatsen en het laatste cijfer vooraan te plaatsen. Dit levert een nieuw getal $$d'' = d'_nd'_1d'_2\ldots d'_{n-1}$$ van $$n$$ cijfers op.

De progressiestap bepaalt dus dat het getal $$d$$ in de arithmetische progressie gevolgd wordt door het getal $$d''$$. Om nu de opvolger van het getal $$d''$$ in de arithmetische progressie te bepalen, gebruiken we in de volgende progressiestap niet de verschuivingen $$s$$ maar rollen we die verschuivingen ook naar rechts. Daardoor werken we dus in de volgende progressiestap met de verschuivingen $$s'' = s_ns_1s_2\ldots s_{n-1}$$.

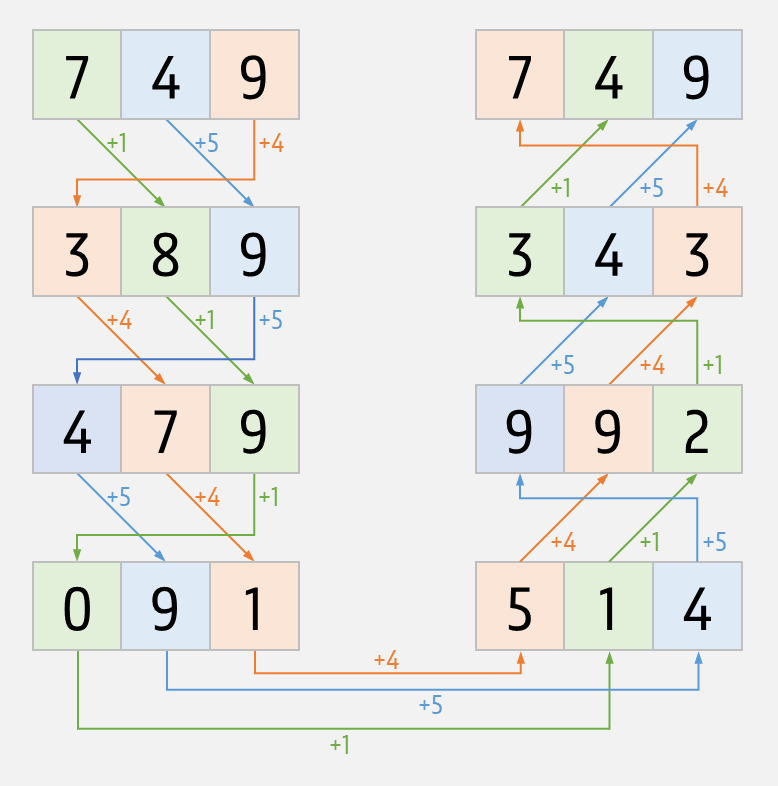
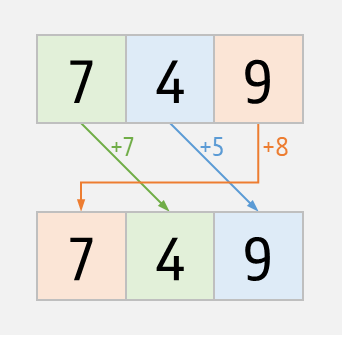
Voor twee getallen $$d$$ en $$s$$ met $$n$$ cijfers heeft de arithmetische progressie van $$d$$ met verschuivingen $$s$$ een cyclisch karakter. Het aantal progressiestappen waarna we terug bij het eerste getal $$d$$ uitkomen, noemen we de periode van de arithmetische expressie. Zo komen we in de arithmetische progressie van 749 met verschuivingen 123 bijvoorbeeld na 30 progressiestappen terug bij getal 749 uit. Dit is ook de maximale periode, want voor een getal met $$n$$ cijfers is de periode altijd kleiner of gelijk aan $$10 \times n$$. Er zijn echter ook kortere periodes mogelijk. Zo heeft de arithmetische expressie van 749 met verschuivingen 154 bijvoorbeeld een periode van 7, en met verschuivingen 758 krijgen we zelfs na één progressiestap terug het getal 749.

De arithmetische progressie van 749 met verschuivingen 154 heeft periode 7.

De arithmetische progressie van 749 met verschuivingen 758 heeft periode 1.

Gevraagd wordt:

Schrijf een functie rollen waaraan een getal $$d = d_1d_2\ldots d_n$$ van $$n$$ cijfers moet doorgegeven worden. De functie moet het getal $$d_nd_1d_2\ldots d_{n-1}$$ van $$n$$ cijfers teruggeven dat bekomen wordt door alle cijfers van $$d$$ één positie naar rechts te verplaatsen en het laatste cijfer vooraan te plaatsen.
Schrijf een functie verschuiven waaraan twee getallen $$d = d_1d_2\ldots d_n$$ en $$s = s_1s_2\ldots s_n$$ van $$n$$ cijfers moeten doorgegeven worden. De functie moet het getal $$d'_1d'_2\ldots d'_n$$ van $$n$$ cijfers teruggeven, waarbij $$d'_i = (d_i + s_i)\!\!\!\!\mod{10}$$ voor $$i = 1, 2, \ldots, n$$) en waarbij $$\text{mod}$$ de bewerking is die de rest na deling bepaalt.
Schrijf een functie progressie waaraan drie argumenten moeten doorgegeven worden: i) een getal $$d = d_1d_2\ldots d_n$$ van $$n$$ cijfers, ii) een getal $$s = s_1s_2\ldots s_n$$ van $$n$$ cijfers en iii) een getal $$m \in \mathbb{N}$$ (int). De functie moet het getal van $$n$$ cijfers teruggeven dat na $$m$$ progressiestappen bekomen wordt in de arithmetische progressie van $$d$$ met verschuivingen $$s$$.
Schrijf een functie periode waaraan twee getallen $$d = d_1d_2\ldots d_n$$ en $$s = s_1s_2\ldots s_n$$ van $$n$$ cijfers moeten doorgegeven worden. De functie moet de periode (int) teruggeven van de arithmetische progressie van $$d$$ met verschuivingen $$s$$.

Voorbeeld

        >>> rollen('749')
'974'
>>> rollen('48839')
'94883'

>>> verschuiven('749', '123')
'862'
>>> verschuiven('52736', '97563')
'49299'

>>> progressie('749', '123', 1)
'286'
>>> progressie('749', '123', 2)
'859'
>>> progressie('749', '123', 3)
'008'
>>> progressie('749', '123', 30)
'749'
>>> progressie('52736', '97563', 1)
'94929'
>>> progressie('52736', '97563', 2)
'52367'
>>> progressie('52736', '97563', 3)
'21523'
>>> progressie('52736', '97563', 9)
'52736'

>>> periode('749', '123')
30
>>> periode('749', '154')
7
>>> periode('749', '758')
1
>>> periode('52736', '97563')
9
>>> periode('416275', '869241')
21