Het bepalen van het volledige genoom van een organisme (genoomsequenering) is één van de hoekstenen van de bioinformatica. Helaas beschikken we nog steeds niet over microscopische technologie die toelaat om tot op nucleotideniveau in te zoomen en zo de reeks nucleotiden van een genoom één voor één af te lezen. Onderzoekers beschikken echter wel over chemische methoden die kunnen toegepast worden voor het genereren en identificeren van kortere DNA fragmenten. In deze context worden de korte fragmenten reads genoemd. Nadat we een grote collectie van reads geïdentificeerd hebben uit meerdere kopieën van hetzelfde genoom, blijft de uitdaging om het genoom te reconstrueren uit deze korte stukjes DNA. Dit proces wordt genoomassemblage genoemd.
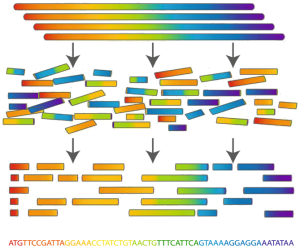
Genoomassemblage is computationeel gezien een extreem moeilijk probleem. Het wordt nog moeilijker doordat heel veel genomen een groot aantal identieke sequenties bevatten die op verschillende plaatsen in het genoom herhaald worden. Dergelijke herhalingen zijn vaak duizenden nucleotiden lang en sommige kunnen op duizenden verschillende plaatsen in het genoom voorkomen. Dit komt vooral voor in de grote genomen van planten en dieren. Hierdoor is het vaak niet mogelijk om het volledige genoom te reconstrueren, en eindigt het assemblageproces met een aantal grote stukken van het genoom die in deze context contigs genoemd worden.
Opgave
Om de kwaliteit van een genoomassemblage te bepalen (bijvoorbeeld om twee verschillende assemblage-algoritmen te vergelijken, die elk afzonderlijk contigs bepaald hebben vertrekkend van dezelfde verzameling reads) wordt vaak gebruikgemaakt van de N50 statistiek.
Stel dat we voor een genoom van lengte $$g$$ na assemblage een reeks contigs hebben bekomen, en dat we de lengtes van die contigs sorteren van groot naar klein. Daarna beginnen we de lengtes bij elkaar op te tellen (in dalende volgorde). De eerste lengte die ervoor zorgt dat de som groter of gelijk wordt aan $$\frac{g}{2}$$ (de helft van de lengte van het genoom) levert ons een eerste benadering van de N50 statistiek op. Een tweede benadering wordt bekomen door dezelfde procedure toe te passen, maar dan door de contiglengtes in stijgende volgorde bij elkaar op te tellen. De N50 statistiek is dan het gemiddelde van deze twee benaderingen. Soms is de lengte van het genoom niet gekend. In dat geval neemt men doorgaans de som van alle contiglengtes als schatting van de genoomlengte $$g$$.
Stel bijvoorbeeld dat de lijst van contiglengtes gelijk is aan $$[2, 2, 2, 3, 3, 4, 8, 8]$$. We kunnen de genoomlengte schatten als $$2 + 2 + 2 + 3 + 3 + 4 + 8 + 8 = 32$$. In dit geval levert een eerste benadering van de N50 statistiek (dalende volgorde) de waarde 8 op, want $$8 + 8 = 16 \geq \frac{32}{2}$$. Een tweede benadering (stijgende volgorde) levert de waarde 4 op, want $$2 + 2 + 2 + 3 + 3 + 4 = 16 \geq \frac{32}{2}$$. Op basis van deze twee benaderingen kunnen we de N50 statistiek dus berekenen als $$\frac{8 + 4}{2}$$ = 6.
Gevraagd wordt:
Schrijf een functie N50_dalend waaraan een collectie (een lijst, tuple, verzameling, …) van natuurlijke getallen moet doorgegeven worden. Deze getallen stellen de lengtes voor van de contigs die bekomen worden na genoomassemblage. De functie heeft een tweede optionele parameter grootte waaraan de genoomgrootte kan doorgegeven worden. Indien geen waarde wordt doorgegeven aan deze parameter, dan wordt de som van de contiglengtes gebruikt als schatting voor de genoomgrootte. De functie moet de benadering van de N50 statistiek teruggeven (als natuurlijk getal), die resulteert als de procedure wordt toegepast die hierboven staat beschreven en waarbij een lopende som gebruikt wordt over de contiglengtes die in dalende volgorde gesorteerd zijn.
Schrijf een functie N50_stijgend die dezelfde parameters heeft als de functie N50_dalend, met dezelfde betekenis. De functie moet de benadering van de N50 statistiek teruggeven (als natuurlijk getal), die resulteert als de procedure wordt toegepast die hierboven staat beschreven en waarbij een lopende som gebruikt wordt over de contiglengtes die in stijgende volgorde gesorteerd zijn.
Gebruik de functies N50_dalend en N50_stijgend om een functie N50 te schrijven die dezelfde parameters heeft als de twee vorige functies, met dezelfde betekenis. De functie moet de N50 statistiek voor de gegeven collectie van contiglengtes teruggeven als een floating point getal.
Voorbeeld
>>> contigs = (2, 2, 2, 3, 3, 4, 8, 8)
>>> N50_dalend(contigs)
8
>>> N50_stijgend(contigs)
4
>>> N50(contigs)
6.0
>>> contigs = (5, 8, 6, 4, 6, 1, 1)
>>> N50_dalend(contigs, grootte=40)
6
>>> N50_stijgend(contigs, grootte=40)
6
>>> N50(contigs, 40)
6.0