Een woordvierkant bestaat uit een reeks woorden die in een vierkant rooster uitgeschreven worden, zodat hetzelfde woord zowel horizontaal als verticaal kan uitgelezen worden in de overeenkomstige rij en kolom van het rooster. Het aantal woorden — dat gelijk is aan het aantal letters van elk woord — wordt de orde van het vierkant genoemd. Dit is bijvoorbeeld een woordvierkant van orde 3:
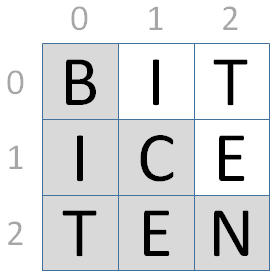
In vergelijking met kleine woordvierkanten, zijn grote woordvierkanten verschrikkelijk moeilijk te construeren. Het grootste woordvierkant dat men tot op vandaag heeft kunnen opstellen, bestaat uit 9-letterwoorden:

Puzzelfanaten zijn al meer dan 100 jaar op zoek naar een perfect $$10 \times 10$$ woordvierkant. Deze taak leek schier onmogelijk, totdat Dmitri Borgmann in 1972 onverwacht botste op een artikel van David Livingstone in een Afrikaanse krant, waarvan de editie van 26 september 1872 het volgende tekstfragment bevatte:
Through forest, along the side of a sedgy valley. Cross its head-water, which has rust of iron in it, then west and by south. The forest has very many tsetse. Zebras calling loudly, and Senegal long claw in our camp at dawn, with its cry, 'O-o-o-o-o-o-o-o-o-o.'
Meer was er niet nodig. Voorzien van een pen kon de geelbuiklangkauw (Macronyx flavigaster) voor Livingstone een perfect $$10 \times 10$$ woordvierkant neergeschreven hebben:

We moesten vaker te rade gaan bij andere soorten. Elke langkauw had ons deze oplossing op een dienblaadje kunnen aanbieden — inderdaad, het is het enige woordvierkant dat die vogel kan maken!

Opgave
Omdat woordvierkanten symmetrisch zijn ten opzichte van de hoofddiagonaal, volstaat het om een woordvierkant te beschrijven door de letters op en onder de hoofddiagonaal uit te lezen van links naar rechts, en van boven naar onder. Het woordvierkant van orde 3 dat in de inleiding als voorbeeld gegeven werd, kan op die manier beschreven worden aan de hand van de zes letters BICTEN. Algemeen geldt dat een woordvierkant van orde $$n$$ kan beschreven worden aan de hand van $$\frac{n(n + 1)}{2}$$ letters op of onder de hoofddiagonaal. Je opdracht bestaat erin een klasse Woordvierkant te definiëren waarmee woordvierkanten kunnen voorgesteld worden in Python. Deze klasse moet minstens de volgende methoden ondersteunen:
Een initialisatiemethode waaraan twee argumenten moeten doorgegeven worden: de orde van het woordvierkant en de letters op en onder de hoofddiagonaal, uitgelezen van links naar rechts en van boven naar onder. Indien het gegeven aantal letters op en onder de hoofddiagonaal niet correspondeert met de gegeven orde, dan moet de methode een AssertionError opwerpen met de boodschap ongeldig vierkant.
Een methode letter waaraan de rij- en kolomindex van een positie binnen het woordvierkant moeten doorgegeven worden. De methode moet de letter (in hoofdlettervorm) teruggeven die gevonden wordt op de aangegeven positie in het woordvierkant. Hierbij worden de rijen van boven naar onder, en de kolommen van links naar rechts geïndexeerd vanaf nul. Indien de gegeven argumenten niet corresponderen met een positie binnen het vierkant rooster, dan moet de methode een AssertionError opwerpen met de boodschap ongeldige index.
Een methode woord waaraan een rij- of kolomindex van het woordvierkant moet doorgegeven worden (zelfde indexering als bij voorgaande methode). De methode moet het woord (in hoofdletters) teruggeven dat in het woordvierkant gevonden wordt op de aangegeven rij/kolom. Indien de gegeven index niet correspondeert met een rij/kolom in het woordvierkant, dan moet de methode een AssertionError opwerpen met de boodschap ongeldige index.
Een methode geldig waaraan de locatie van een tekstbestand moet doorgegeven worden. Dit tekstbestand bevat een lijst van woorden, elk op een afzonderlijke regel. De methode moet een Booleaanse waarde teruggeven, die aangeeft of alle woorden uit het woordvierkant voorkomen in de gegeven lijst van woorden. Bij de vergelijking van de woorden uit het woordvierkant en de gegeven woordenlijst mag geen onderscheid gemaakt worden tussen hoofdletters en kleine letters.
Bovendien moet het mogelijk zijn om met de ingebouwde functie print een stringvoorstelling uit te schrijven van elk object van de klasse Woordvierkant. In deze stringvoorstelling worden de letters van het woordvierkant rij per rij uitgeschreven, zoals aangegeven in onderstaande voorbeelden.
Voorbeeld
Bij onderstaande voorbeeldsessie gaan we ervan uit dat het tekstbestand words.txt zich in de huidige directory bevindt.
>>> vierkant = Woordvierkant(3, 'bicten')
>>> vierkant.letter(1, 0)
'I'
>>> vierkant.letter(1, 1)
'C'
>>> vierkant.letter(1, 2)
'E'
>>> vierkant.woord(1)
'ICE'
>>> print(vierkant)
BIT
ICE
TEN
>>> vierkant.geldig('words.txt')
True
>>> vierkant.letter(1, 3)
Traceback (most recent call last):
AssertionError: ongeldige index
>>> vierkant.woord(3)
Traceback (most recent call last):
AssertionError: ongeldige index
>>> vierkant = Woordvierkant(3, 'ABCDE')
Traceback (most recent call last):
AssertionError: ongeldig vierkant
>>> vierkant = Woordvierkant(9, 'ACRHEXANABLINOLADDLEHSERINETINITIATOASCENDERS')
>>> vierkant.woord(1)
'CRENIDENS'
>>> vierkant.woord(7)
'INITIATOR'
>>> print(vierkant)
ACHALASIA
CRENIDENS
HEXANDRIC
ANABOLITE
LINOLENIN
ADDLEHEAD
SERINETTE
INITIATOR
ASCENDERS
>>> vierkant.geldig('words.txt')
True
>>> vierkant = Woordvierkant(4, 'ABCDEFGHIJ')
>>> print(vierkant)
ABDG
BCEH
DEFI
GHIJ
>>> vierkant.geldig('words.txt')
False