Bij een 3 × 3 matrix kan men de determinant berekenen met behulp van de regel van Sarrus.
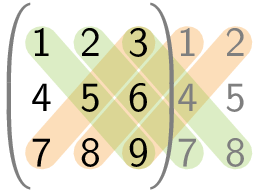
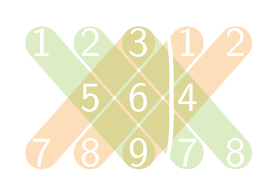
Voor een matrix A van de vorm:
\[\sf A = \begin{pmatrix} \sf a_{11} & \sf a_{12} & \sf a_{13}\\ \sf a_{21} & \sf a_{22} & \sf a_{23}\\ \sf a_{31} & \sf a_{32} & \sf a_{33} \end{pmatrix}\]gebruikt men de regel van Sarrus door de eerste twee kolommen rechts aan de matrix toe te voegen, en nadien berekent met de producten van de hoofd- en nevendiagonalen. Dit resulteert in:
\[\mathsf{A = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} +a_{13}a_{21}a_{32} - a_{31}a_{22}a_{13} - a_{32}a_{23}a_{11} - a_{33}a_{21}a_{12}}\]Gevraagd
Schrijf een functie sarrus(matrix) die de determinant berekent met behulp van deze regel.
Voorbeeld
>>> sarrus([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
0
Want \(\mathsf{1\cdot 5 \cdot 9 + 2\cdot 6 \cdot 7 + 3\cdot 4 \cdot 8 - 7\cdot 5 \cdot 3 -8\cdot 6\cdot 1 - 9 \cdot 4 \cdot 2 = 0 }\)