Zoek de fouten

Er staat al code klaar, maar er zitten nog fouten in. Verbeter al de fouten en dien in om feedback te krijgen.

Een kwadratische vergelijking is een vergelijking van de vorm

\[ax^2 + bx + c = 0\]

, waarin \(a, b, c \in \mathbb{R}\) en \(a \neq 0\).

De grootheid

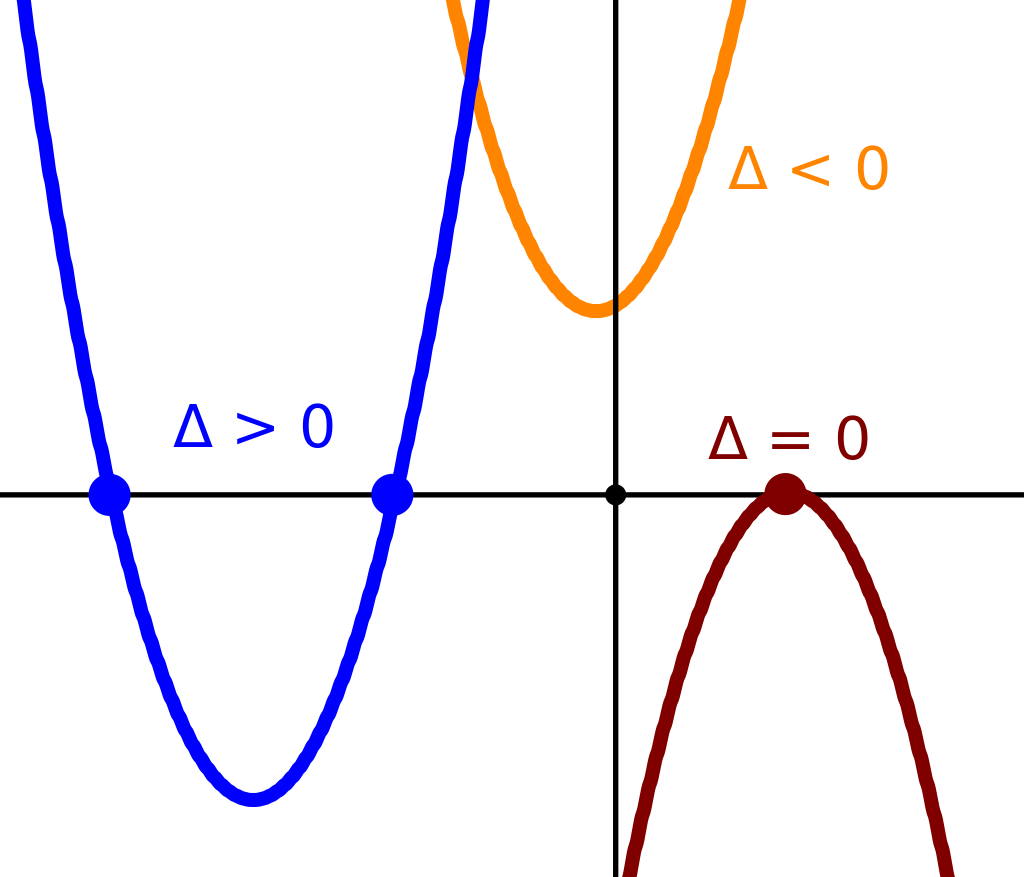
\[\Delta = b^2 - 4ac\]

wordt de discriminant van de kwadratische vergelijking genoemd. Het teken van \(\Delta\) bepaalt het aantal reële oplossingen. Als \(\Delta > 0\) dan zijn er twee verschillende reële oplossingen (\(x_1 \neq x_2\)). De reële oplossingen kunnen bepaald worden met de zogenaamde wortelformule:

\[x_{1} = \frac{-b - \sqrt{\Delta}}{2a}\ \ \ \text{en}\ \ \ x_{2} = \frac{-b + \sqrt{\Delta}}{2a}\]

Invoer

De drie parameters \(a\), \(b\) en \(c\) van een kwadratische vergelijking, elk op een afzonderlijke regel.

Uitvoer

Je mag er van uitgaan dat het in deze oefening altijd een geldige vierkantsvergelijking is met telkens twee oplossingen (discriminant is altijd groter dan 0, \(\Delta > 0\)), die uitgeprint moeten worden. Vermeld altijd eerst \(x_1\) en op een volgende regel \(x_2\).

Voorbeeld 1

De nulpunten van \(1x^2 + 4x -5\) zijn \(x_1 = -5\) en \(x_2 = 1.0\).

Invoer:

1
4
-5

Uitvoer:

Nulpunt 1:  -5.0
Nulpunt 2:  1.0

Voorbeeld 2

De nulpunten van \(2x^2 + 5x -3\) zijn \(x_1 = -3\) en \(x_2 = -0.5\).

Invoer:

2
5
-3

Uitvoer:

Nulpunt 1:  -3.0
Nulpunt 2:  0.5