Speleologie is een tak van de aardwetenschappen die zich bezighoudt met de studie van grotten. Hoewel speleologie een serieuze wetenschap is, komt er bij het verkennen van grotten ook een element van sportiviteit, avontuur en moed kijken. Het verkennen van grotten, zeker als zij nog onvolledig bekend zijn, is zeker niet zonder gevaar en vereist vaardigheid en training.

Als wetenschap bestudeert de speleologie onder andere de geologie (het ontstaan van gesteentelagen, grotten en druipsteen), de hydrologie (onderaardse waterlopen), de biologie (de fauna en flora in een grot), de paleontologie (overblijfselen van uitgestorven dieren in grotten) en de archeologie (grotschilderingen en werktuigen uit de prehistorie). Ook de geologie van streken waar grotten voorkomen is onderwerp van studie. De speleologie als sport kunnen we vergelijken met de bergsport, omdat voor een groot deel dezelfde technieken en materialen gebruikt worden.

Opgave

Als onderdeel van je speleologietraining krijg je de plattegrond van een grot die bestaat uit een aantal zalen. De zalen van de grot zijn gerangschikt in een rechthoekig $$m \times n$$ rooster met $$m$$ rijen en $$n$$ kolommen. De grot heeft slechts één ingang en één uitgang, en vanuit elke zaal kan je naar elk van de naburige zalen ten noorden, zuiden, oosten en westen, tenzij je daarbij tegen de rand van de grot botst. Je opdracht bestaat erin een geldige doorgang te vinden die vertrekt vanaf de zaal waar de ingang van de grot gelegen is, en steeds loopt via een naburige zaal totdat de zaal bereikt wordt waar de uitgang van de grot gelegen is. Hierbij mag elke zaal hoogstens één keer bezocht worden. Bovendien bevat de plattegrond ook aanwijzingen hoeveel zalen de doorgang moet passeren op elke rij en kolom van het rooster.

Als voorbeeld krijg je hieronder de plattegrond van een grot, waarvan de zalen gerangschikt zijn in een $$5 \times 5$$ rooster. Om makkelijk naar de zalen te kunnen verwijzen, nummeren we de rijen oplopend van noord naar zuid en de kolommen van west naar oost, waarbij we steeds beginnen nummeren vanaf nul (grijze getallen op de voorbeeld plattegrond). De grot heeft een ingang in zaal (0,0) en een uitgang in zaal (3, 4). We beschrijven een doorgang als een opeenvolging van letters die aangeven welk van de naburige zalen in een volgende stap bezocht wordt: N (noord), Z (zuid), O (oost) of W (west).

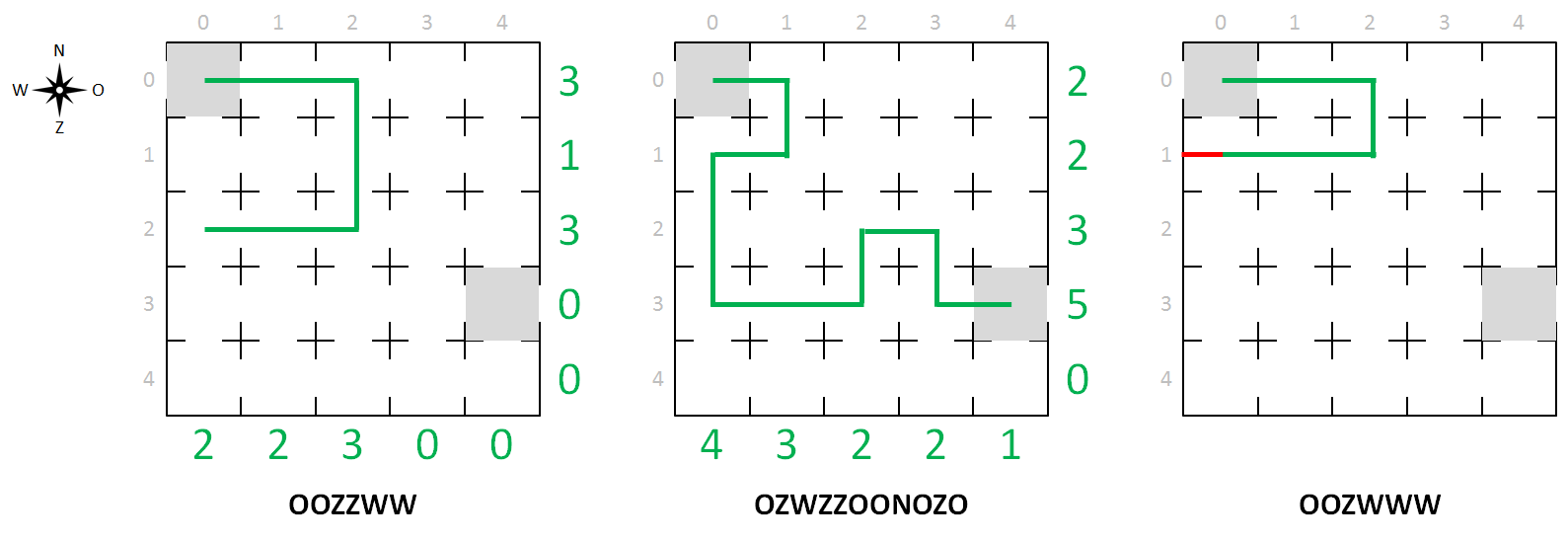
De doorgang OZWZZOONOZO (middelste plattegrond van de figuur) is een doorgang die vanaf de ingang leidt naar de uitgang, waarbij het aantal passages doorheen de rijen en kolommen van de plattegrond wordt aangegeven in het groen. Zo zijn er bijvoorbeeld 2 passages door de meest noordelijke rij en 4 passages door de meest westelijke kolom. Bovendien bezoekt deze doorgang elke zaal hoogstens één keer. De doorgang OOZZWW (linkse plattegrond) is niet geldig omdat die niet naar de uitgang leidt. De doorgang OOZWWW (rechtse plattegrond) is eveneens ongeldig, omdat er tegen de rand van de grot wordt gebotst.

Je opdracht bestaat erin een klasse Grot te schrijven waarvan elk object de plattegrond van een grot voorstelt. De grot bestaat uit een aantal zalen die gerangschikt zijn in een rechthoekig $$m \times n$$ rooster. Naast de posities van de ingang en uitgang, bevat de map ook aanwijzingen hoeveel zalen een geldige doorgang moet passeren op elke rij en kolom van het rooster. Zorg ervoor dat de objecten minstens over de volgende methoden beschikken, waarmee kan nagegaan worden of een gegeven doorgang al dan niet geldig is.

• Een initialisatiemethode waarmee de plattegrond van de grot kan vastgelegd worden, alsook het gewenste aantal passages op elke rij en kolom van het rooster. Aan deze methode moeten vier argumenten doorgegeven worden, waarbij elk argument een reeks (een lijst of een tuple) natuurlijke getallen is. Het eerste argument bevat $$m$$ getallen die aangeven hoeveel passages de gezochte doorgang moet hebben door elke rij (van noord naar zuid) van het rooster. Het tweede argument bevat $$n$$ getallen die aangeven hoeveel passages de gezochte doorgang moet hebben door elke kolom (van west naar oost) van het rooster. De laatste twee argumenten bevatten het rijnummer $$r$$ en kolomnummer $$k$$ van de zalen waar respectievelijk de ingang en de uitgang van de grot gelegen zijn. De initialisatiemethode moet een AssertionError opwerpen met de boodschap ongeldige plattegrond indien minstens één van de volgende voorwaarden niet voldaan is:

  • alle waarden van het eerste argument moeten in het interval $$[0, n]$$ liggen

  • alle waarden van het tweede argument moeten in het interval $$[0, m]$$ liggen 

  • de zalen waarin de ingang en uitgang van de grot gelegen zijn moeten aan de rand van het rooster liggen

• Een methode doorgang waaraan een string moet doorgegeven worden. Deze string bevat een opeenvolging van de letters N (noord), Z (zuid), O (oost) en W (west). Deze letters beschrijven de opeenvolgende verplaatsingen naar naburige zalen die een doorgang maakt, vertrekkende vanaf de zaal waar de ingang van de grot gelegen is. De methode moet de lijst van de posities van de zalen teruggeven in de volgorde waarin ze bezocht worden door de gegeven doorgang. Hierbij wordt de positie van een zaal beschreven door een tuple $$(r, k)$$, waarbij $$r$$ het rijnummer en $$k$$ het kolomnummer van de zaal in het rooster aangeeft. Indien de beschreven doorgang een verplaatsing zou maken waardoor tegen de rand van de grot wordt gebotst, dan moet de methode een AssertionError opwerpen met de boodschap botst tegen rand.

• Een methode passages waaraan een string moet doorgegeven worden met dezelfde betekenis als bij de methode doorgang. Indien deze string een doorgang vanaf de ingang beschrijft, waarbij op een bepaald moment een verplaatsing zou gemaakt worden die tegen de rand van de grot botst, dan moet de methode een AssertionError opwerpen met de boodschap botst tegen rand. De methode moet een tuple teruggeven dat zelf twee tuples bevat, die het aantal passages aangeven die de gegeven doorgang maakt met respectievelijk de rijen (van noord naar zuid) en de kolommen (van west naar oost) van het rooster.

• Een methode geldigeDoorgang waaraan een string moet doorgegeven worden met dezelfde betekenis als bij de methode doorgang. Indien deze string een doorgang vanaf de ingang beschrijft, waarbij op een bepaald moment een verplaatsing zou gemaakt worden die tegen de rand van de grot botst, dan moet de methode een AssertionError opwerpen met de boodschap botst tegen rand. De methode moet een Booleaanse waarde teruggeven, die aangeeft of de gegeven doorgang al dan niet geldig is. Een doorgang is geldig als hij i) eindigt in de zaal waar de uitgang van de grot gelegen is, ii) dezelfde zaal niet meermaals bezoekt, iii) elke rij het opgegeven aantal keer passeert en iv) elke kolom het opgegeven aantal keer passeert.

Voorbeeld

>>> grot = Grot((2, 2, 3, 5, 0), (4, 3, 2, 2, 1), (0, 0), (3, 4))

>>> grot.doorgang('OOZZWW')
[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 1), (2, 0)]
>>> grot.passages('OOZZWW')
((3, 1, 3, 0, 0), (2, 2, 3, 0, 0))
>>> grot.geldigeDoorgang('OOZZWW')
False

>>> grot.doorgang('OZWZZOONOZO')
[(0, 0), (0, 1), (1, 1), (1, 0), (2, 0), (3, 0), (3, 1), (3, 2), (2, 2), (2, 3), (3, 3), (3, 4)]
>>> grot.passages('OZWZZOONOZO')
((2, 2, 3, 5, 0), (4, 3, 2, 2, 1))
>>> grot.geldigeDoorgang('OZWZZOONOZO')
True

>>> grot.doorgang('OOZWWW')
Traceback (most recent call last):
AssertionError: botst tegen rand
>>> grot.passages('OOZWWW')
Traceback (most recent call last):
AssertionError: botst tegen rand
>>> grot.geldigeDoorgang('OOZWWW')
Traceback (most recent call last):
AssertionError: botst tegen rand

>>> grot = Grot((2, 2, 3, 6, 0), (4, 3, 2, 2, 1), (0, 0), (3, 4))
Traceback (most recent call last):
AssertionError: ongeldige plattegrond

>>> grot = Grot((2, 2, 3, 5, 0), (4, 3, 2, 2, 1), (1, 1), (3, 4))
Traceback (most recent call last):
AssertionError: ongeldige plattegrond