Voorbereiding

De module random¹ uit de Standard Python Library kan onder andere gebruikt worden om willekeurige getallen te genereren. De functie random() uit deze module genereert een willekeurig reëel getal uit het interval $$[0, 1[$$. De functie randint(a, b) kan dan weer gebruikt worden om een willekeurig geheel getal te genereren uit het interval $$[a, b]$$. Onderstaande interactieve Python sessie geeft aan de hand van enkele voorbeelden aan hoe je de functies uit de module random kunt gebruiken.

>>> import random
>>> help(random.random)
Help on built-in function random:

random(...)
    random() -> x in the interval [0, 1).
>>> random.random()
0.954131645221452
>>> random.random()
0.3548429482674793

>>> help(random.randint)
Help on method randint in module random:

randint(self, a, b) method of random.Random instance
    Return random integer in range [a, b], including both end points.
>>> random.randint(3, 10)
5
>>> random.randint(3, 10)
8

Omschrijving

Een bol kan voorgesteld worden als de verzameling van alle punten op afstand $$r$$ vanaf het centraal punt $$(0,0,0)$$. Indien $$r=1$$ dan spreekt men van de eenheidsbol. De methode van Marsaglia² kan gebruikt worden om een willekeurig punt op een bol met straal $$r$$ te genereren. In een eerste stap van deze methode wordt een willekeurig punt $$(x_1,y_1)$$ gekozen dat binnen de eenheidscirkel gelegen is. Dit is een punt waarvoor geldt dat $$x_1^2+y_1^2\leq 1$$. Om dit te doen worden willekeurige punten gegenereerd in het 2-bij-2 vierkant $$[-1,1]\times[-1,1]$$ met centrum in $$(0,0)$$, totdat een punt gevonden wordt dat binnen de eenheidscirkel ligt.

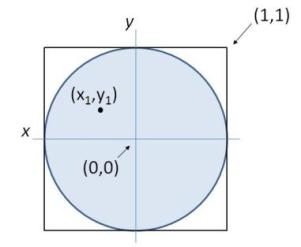
Het punt $$(x_1,y_1)$$ wordt vervolgens gebruikt om op de volgende manier de $$(x,y,z)$$ coördinaten van een willekeurig punt op de bol met straal $$r$$ te bepalen: \[ \begin{aligned} x & = 2 r x_1 \sqrt{1 - x_1^2 - y_1^2} \\ y & = 2 r y_1 \sqrt{1 - x_1^2 - y_1^2} \\ z & = r - 2r(x_1^2 + y_1^2) \end{aligned} \]

Opgave

Schrijf een functie waarmee een willekeurig punt op een bol met straal $$r \in \mathbb{R}$$ kan gegeneerd worden. Aan deze functie kan optioneel een waarde voor $$r$$ doorgegeven worden. Standaard wordt een willekeurig punt op de eenheidsbol gegenereerd. De functie moet als resultaat een tuple met de $$(x,y,z)$$ coördinaten van het willekeurige punt teruggeven.

Voorbeeld

>>> bolcoordinaat()
(0.8208783192500947, 0.24904502507471912, 0.5139410087458212)
>>> bolcoordinaat()
(0.1705946803883025, 0.9853183076681309, 0.006729606022916168)
>>> bolcoordinaat()
(0.5245775493577824, 0.47160784998323607, -0.7088049312356488)

>>> bolcoordinaat(1.2)
(1.006669684101887, 0.41835600224171376, 0.10767730725894864)
>>> bolcoordinaat(5.8)
(0.3653448756504214, 0.8635619785170504, -2.2182839834195476)
>>> bolcoordinaat(4.9)
(0.5245775493577824, 0.47160784998323607, -0.7088049312356488)