Eiwitopvouwing is het fysisch proces waarbij een eiwit1 zich op een snelle en reproduceerbare manier opvouwt tot zijn natieve2 driedimensionale structuur3 waarin het biologisch werkzaam is. Na translatie4 van mRNA5 naar een lineaire keten van aminozuren6 is het eiwit nog een ongevouwen polypeptide7 zonder stabiele structuur (linkerkant van de figuur). Tijdens of na het synthesiseren van de polypeptideketen door een ribosoom8, begint de lineaire keten zich op te vouwen tot zijn driedimensionale structuur (rechterkant van de figuur).
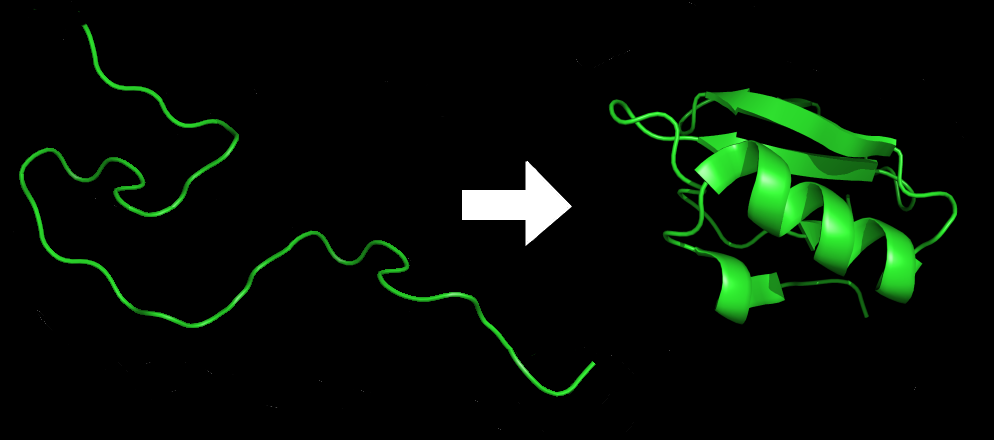
Deze driedimensionale eiwitstructuur wordt volledig bepaald door de lineaire keten van aminozuren (Anfinsen's dogma9), die de primaire structuur genoemd wordt. Sinds het begin van de jaren 60 vormt het begrijpen en simuleren van het eiwitvouwproces een uiterst complexe uitdaging binnen de computationele biologie10.
Het hydrofobe-polaire (HP) model is een sterke vereenvoudiging om ruimtelijk inzicht te krijgen in het proces van eiwitvouwen. Het werd voor het eerst in 1985 voorgesteld door Ken Dill en is het bekendste roostermodel voor eiwitten. Het vertrekt van de waarneming dat hydrofobe interacties tussen aminozuren de drijvende kracht zijn voor het opvouwen van eiwitten. Alle aminozuren worden geclassificeerd als hydrofoob (H) of polair (P) en het opvouwen van een eiwit wordt gedefinieerd als een zelfvermijdende wandeling in een tweedimensionaal of driedimensionaal rooster. Het hydrofobe effect wordt in het HP-model nagebootst door een negatief gewicht toe te kennen aan interacties tussen aangrenzende hydrofobe aminozuren en te zoeken naar opvouwingen die een minimaal gewicht opleveren.
Opgave
De primaire structuur van een eiwit wordt voorgesteld als een reeks (str) van hydrofobe (H) en polaire (P) aminozuren, bijvoorbeeld HHPPHHHPHHPH. De volgorde van de aminozuren is belangrijk: HPP en PPH zijn verschillende eiwitten.
In de natuur worden eiwitten driedimensionaal opgevouwen, maar voor de eenvoud kijken we hier naar eiwitopvouwing in twee dimensies. In het HP-model bezetten de aminozuren van een opgevouwen eiwit de cellen van een rooster: hoogstens één aminozuur per cel. Ze worden zo opgevouwen dat het aantal HH-contactpunten zo groot mogelijk is, omdat dit energetisch voordelig is. Onderstaande figuren tonen twee mogelijke manieren waarop het voorbeeldeiwit kan opgevouwen worden. De blauwe cel geeft telkens de positie van het eerste aminozuur van het eiwit aan. De groene lijn geeft de opeenvolging van de aminozuren van het eiwit aan. De rode stippen duiden de HH-contactpunten aan.
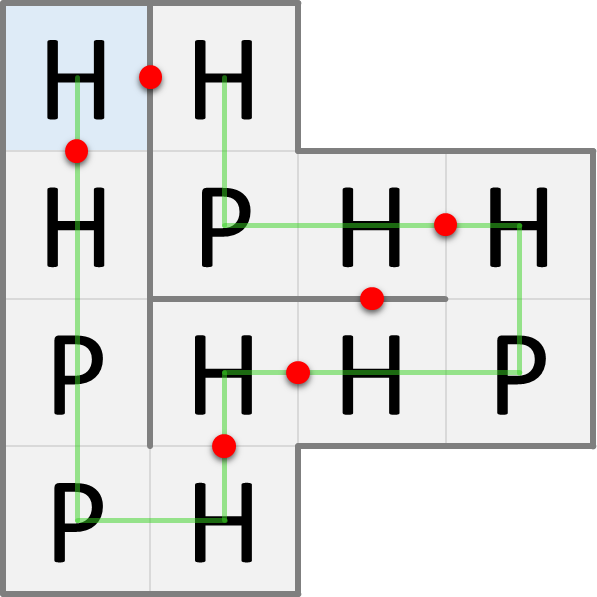
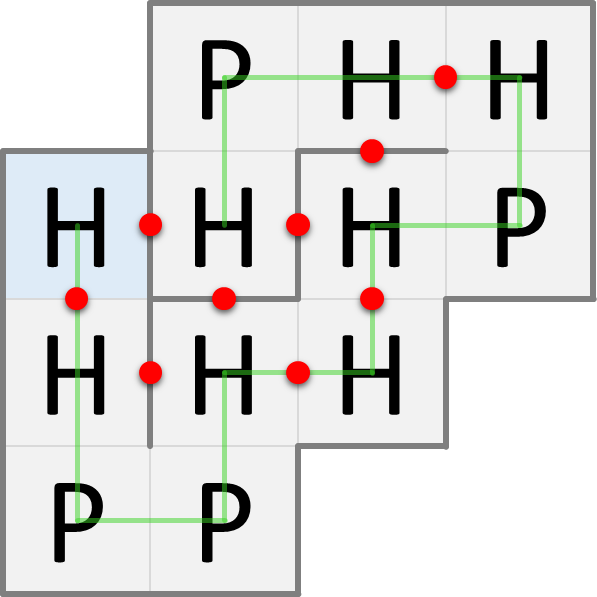
De opvouwing aan de linkerkant heeft slechts 6 HH-contactpunten, terwijl de opvouwing aan de rechterkant 9 HH-contactpunten heeft. Het maximaal aantal HH-contactpunten dat voor dit eiwit kan bekomen worden is 9, waardoor de rechtste opvouwing diegene is die in de natuur zal voorkomen volgens het HP-model.
We duiden de positie van elke cel in een rooster aan met een paar coördinaten $$(x, y)$$ (tuple), waarbij $$x \in \mathbb{N}$$ (int) het kolomnummer en $$y$$ (int) het rijnummer aanduidt. Elke cel heeft vier buren die respectievelijk ten noorden (N), ten oosten (O), ten zuiden (Z) en ten westen (W) liggen. De richtingen waarin deze vier buren liggen, worden met een hoofdletter (str) aangeduid zoals aangegeven in voorgaande oplijsting. Dit is het verband tussen de coördinaten van een cel en die van zijn buren:
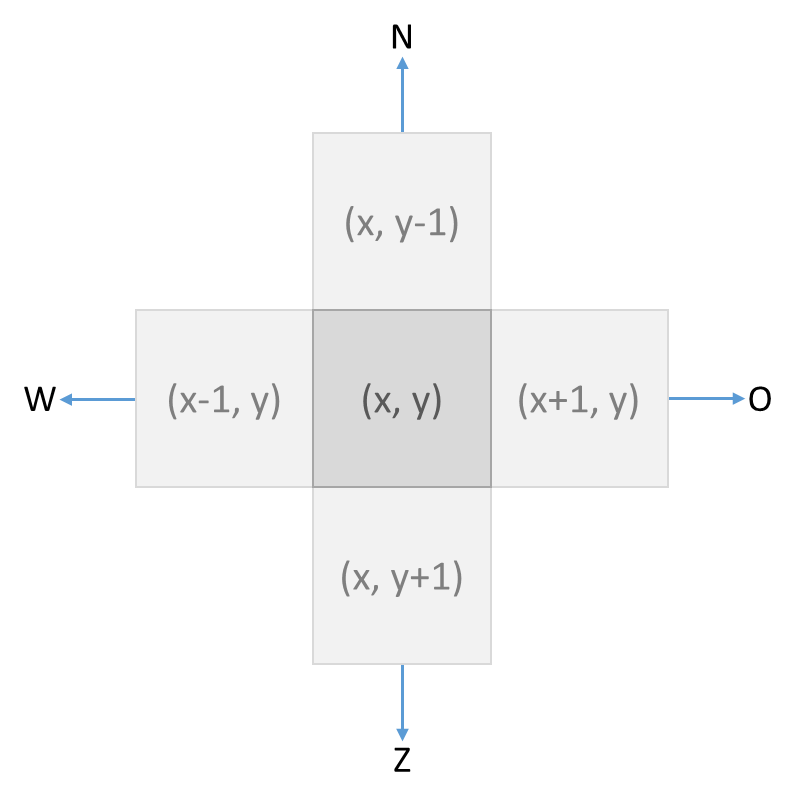
Een mogelijke opvouwing van een eiwit kan dan voorgesteld worden als een reeks (str) richtingen van naburige cellen waar telkens het volgende aminozuur van het eiwit te vinden is. We spreken af dat de cel met het eerste aminozuur op positie $$(0, 0)$$ in het rooster ligt. De mogelijke opvouwing die we hierboven aan de linkerkant gegeven hebben, wordt dan voorgesteld als ZZZONOONWWN en correspondeert met de posities van de opeenvolgende aminozuren die hieronder aan de linkerkant weergegeven worden. De mogelijke opvouwing die we hierboven aan de rechterkant gegeven hebben, wordt voorgesteld als ZZONONONWWZ en correspondeert met de posities van de opeenvolgende aminozuren die hieronder aan de rechterkant weergegeven worden.
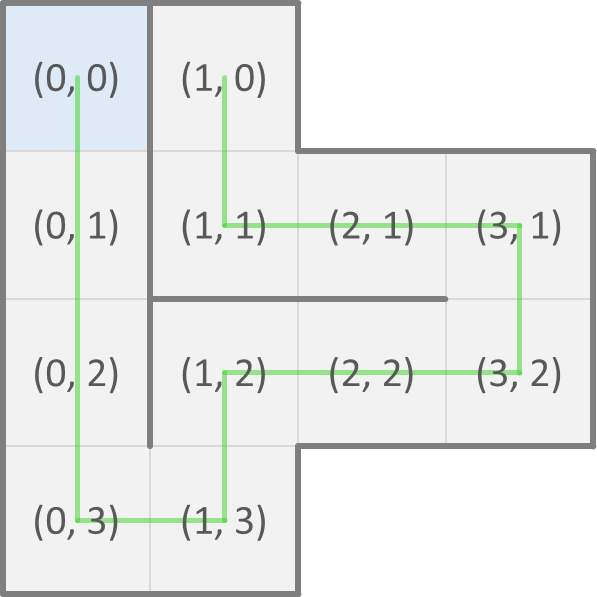
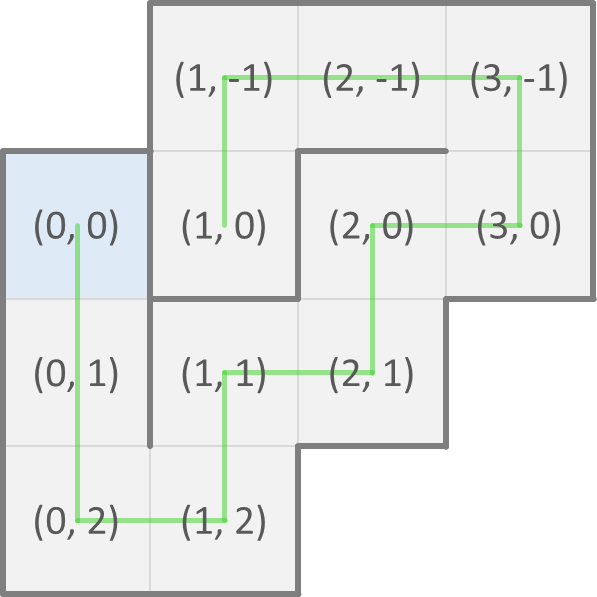
Een opvouwing die zichzelf kruist (die met andere woorden dezelfde positie twee keer bezoekt) is ongeldig. Gevraagd wordt:
-
Schrijf een functie posities waaraan een mogelijke opvouwing (str) van een eiwit moet doorgegeven worden. De functie moet een lijst (list) teruggeven met de posities van de opeenvolgende aminozuren in de gegeven opvouwing.
-
Schrijf een functie opvouwen waaraan twee argumenten moeten doorgegeven worden: i) een mogelijke opvouwing (str) van een eiwit en ii) de primaire structuur (str) van het eiwit. De functie moet een dictionary (dict) teruggeven die de positie van elke cel die volgens de gegeven opvouwing bezet wordt, afbeeldt op de classificatie van het aminozuur in die cel.
-
Schrijf een functie isbuur waaraan de posities van twee cellen in een rooster moeten doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of de twee cellen buren zijn van elkaar.
-
Schrijf een functie contactpunten waaraan twee argumenten moeten doorgegeven worden: i) een mogelijke opvouwing (str) van een eiwit en ii) de primaire structuur (str) van het eiwit. De functie heeft ook nog een derde optionele parameter model waaraan een string (str) met twee hoofdletters kan doorgegeven worden, die aangeven of twee buurcellen hydrofobe (H) of polaire (P) aminozuren moeten bevatten (standaardwaarde: 'HH'). De functie moet teruggeven hoeveel (int) buurcellen er in de opvouwing voorkomen waarvan de ene cel behoort tot de ene klasse van het model en de andere tot de andere klasse van het model. Daarbij maakt de volgorde niet uit: bij model='HH' moeten beide buurcellen hydrofobe aminozuren bevatten, bij model='PP' moeten beide buurcellen polaire aminozuren bevatten en bij model='HP' en model='PH' (deze twee modellen zijn equivalent) moet de ene buurcel een hydrofoob aminozuur en de andere een polair aminozuur bevatten.
Als aan de functies posities, opvouwen en contactpunten een mogelijke opvouwing wordt doorgegeven die ongeldig is, dan moeten ze een AssertionError opwerpen met de boodschap ongeldige opvouwing.
Voorbeeld
>>> posities('ZZZONOONWWN')
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 3), (1, 2), (2, 2), (3, 2), (3, 1), (2, 1), (1, 1), (1, 0)]
>>> posities('ZZONONONWWZ')
[(0, 0), (0, 1), (0, 2), (1, 2), (1, 1), (2, 1), (2, 0), (3, 0), (3, -1), (2, -1), (1, -1), (1, 0)]
>>> posities('ZZOONNWWWNW')
Traceback (most recent call last):
AssertionError: ongeldige opvouwing
>>> opvouwen('ZZZONOONWWN', 'HHPPHHHPHHPH')
{(0, 0): 'H', (0, 1): 'H', (0, 2): 'P', (0, 3): 'P', (1, 3): 'H', (1, 2): 'H', (2, 2): 'H', (3, 2): 'P', (3, 1): 'H', (2, 1): 'H', (1, 1): 'P', (1, 0): 'H'}
>>> opvouwen('ZZONONONWWZ', 'HHPPHHHPHHPH')
{(0, 0): 'H', (0, 1): 'H', (0, 2): 'P', (1, 2): 'P', (1, 1): 'H', (2, 1): 'H', (2, 0): 'H', (3, 0): 'P', (3, -1): 'H', (2, -1): 'H', (1, -1): 'P', (1, 0): 'H'}
>>> opvouwen('ZZOONNWWWNW', 'HHPPHHHPHHPH')
Traceback (most recent call last):
AssertionError: ongeldige opvouwing
>>> isbuur((3, 4), (4, 3))
False
>>> isbuur((3, 4), (4, 4))
True
>>> contactpunten('ZZZONOONWWN', 'HHPPHHHPHHPH')
6
>>> contactpunten('ZZONONONWWZ', 'HHPPHHHPHHPH')
9
>>> contactpunten('ZZZONOONWWN', 'HHPPHHHPHHPH', 'PP')
1
>>> contactpunten('ZZONONONWWZ', 'HHPPHHHPHHPH', model='HP')
6
>>> contactpunten('ZZOONNWWWNW', 'HHPPHHHPHHPH')
Traceback (most recent call last):
AssertionError: ongeldige opvouwing