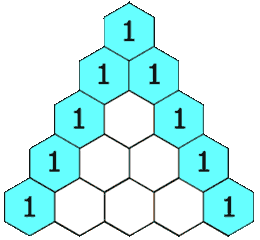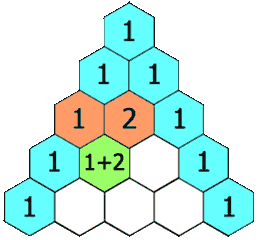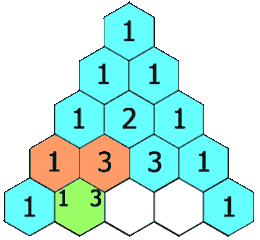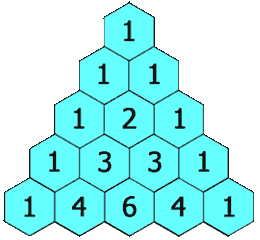
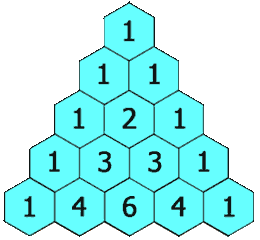
Waarschijnlijk heb je ooit wel al eens gehoord van de driehoek van Pascal. Deze driehoek wordt op de volgende manier opgebouwd. Helemaal bovenaan schrijf je het getal 1. De volgende rij van de driehoek wordt telkens gevormd door op elke positie de som van de twee bovenliggende getallen te schrijven. Indien het getal linksboven of rechtsboven ontbreekt, dan vervang je het door een denkbeeldige nul. Hieronder tonen we alvast hoe de eerste vijf rijen van de driehoek opgebouwd worden.
Weinigen weten echter dat we eigenlijk zouden moeten spreken van het vierkant van Pascal. Blaise Pascal (1623-1662) — de Franse wiskundige naar wie de driehoek vernoemd is — rangschikte de getallen immers zelf in de vorm van een vierkant. De constructie van het vierkant verloopt analoog aan deze van de driehoek. Kies een getal $$n \in \mathbb{N}_0$$. Vul alle posities op de eerste rij en de eerste kolom op met het getal $$n$$. Doorloop daarna de overige cellen van links naar rechts en van boven naar onder, en vul elke cel met de som van de getallen in de twee naburige cellen links en boven. Hieronder tonen we het vierkant van Pascal met vier rijen en vier kolommen, waarbij $$n = 1$$.
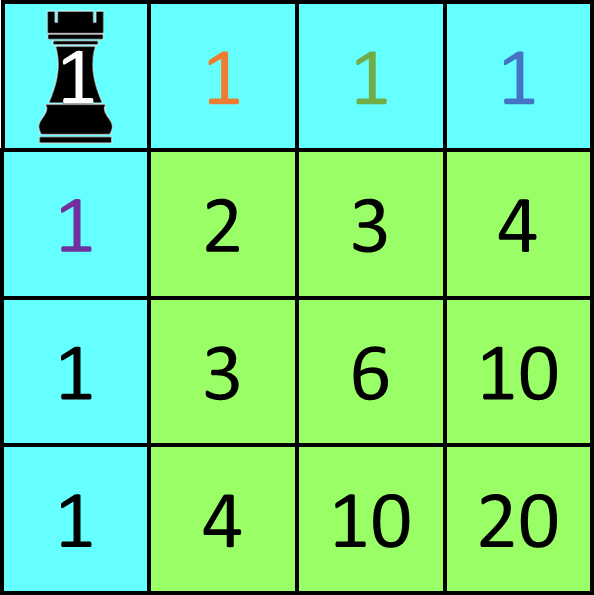
Een eigenschap van het vierkant (resp. de driehoek) van Pascal is dat elk getal aangeeft hoeveel verschillende paden je kan volgen vanaf de cel linksboven het vierkant (resp. de cel bovenaan de driehoek) naar de cel waarin het getal staat, als je enkel naar rechts en naar beneden (resp. naar linksonder en naar rechtsonder) mag bewegen. In het bovenstaande vierkant kan je bijvoorbeeld de cel met het getal 4 op de tweede rij bereiken op vier mogelijke manieren: 1–1–1–4, 1–1–3–4, 1–2–3–4 en 1–2–3–4.
Opgave
-
Schrijf een functie vierkant waaraan een getal $$m \in \mathbb{N}_0$$ moet doorgegeven worden. De functie heeft ook nog een tweede optionele parameter waaraan een getal $$n \in \mathbb{N}_0$$ kan doorgegeven worden (standaardwaarde: $$n=1$$). De functie moet een lijst van lijsten teruggeven die een vierkant van Pascal voorstelt met $$m$$ rijen en $$m$$ kolommen, waarvan de eerste rij en de eerste kolom ingevuld worden met het getal $$n$$.
-
Schrijf een functie paden waaraan een getal $$m \in \mathbb{N}_0$$ moet doorgegeven worden. De functie heeft ook nog een tweede optionele parameter waaraan een getal $$n \in \mathbb{N}_0$$ kan doorgegeven worden (standaardwaarde: $$n=1$$). De functie moet een stringvoorstelling teruggeven van het vierkant van Pascal met $$m$$ rijen en $$m$$ kolommen, waarvan de eerste rij en de eerste kolom ingevuld worden met het getal $$n$$. In deze stringvoorstelling moet elk getal rechts uitgelijnd worden over $$p + 1$$ posities, waarbij $$p$$ het aantal cijfers is in het getal rechts onderaan het vierkant.
Voorbeeld
>>> vierkant(3)
[[1, 1, 1], [1, 2, 3], [1, 3, 6]]
>>> vierkant(3, 100)
[[100, 100, 100], [100, 200, 300], [100, 300, 600]]
>>> vierkant(4)
[[1, 1, 1, 1], [1, 2, 3, 4], [1, 3, 6, 10], [1, 4, 10, 20]]
>>> print(paden(3))
1 1 1
1 2 3
1 3 6
>>> print(paden(3, 100))
100 100 100
100 200 300
100 300 600
>>> print(paden(4))
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
>>> print(paden(6))
1 1 1 1 1 1
1 2 3 4 5 6
1 3 6 10 15 21
1 4 10 20 35 56
1 5 15 35 70 126
1 6 21 56 126 252
>>> print(paden(8))
1 1 1 1 1 1 1 1
1 2 3 4 5 6 7 8
1 3 6 10 15 21 28 36
1 4 10 20 35 56 84 120
1 5 15 35 70 126 210 330
1 6 21 56 126 252 462 792
1 7 28 84 210 462 924 1716
1 8 36 120 330 792 1716 3432
>>> print(paden(10))
1 1 1 1 1 1 1 1 1 1
1 2 3 4 5 6 7 8 9 10
1 3 6 10 15 21 28 36 45 55
1 4 10 20 35 56 84 120 165 220
1 5 15 35 70 126 210 330 495 715
1 6 21 56 126 252 462 792 1287 2002
1 7 28 84 210 462 924 1716 3003 5005
1 8 36 120 330 792 1716 3432 6435 11440
1 9 45 165 495 1287 3003 6435 12870 24310
1 10 55 220 715 2002 5005 11440 24310 48620