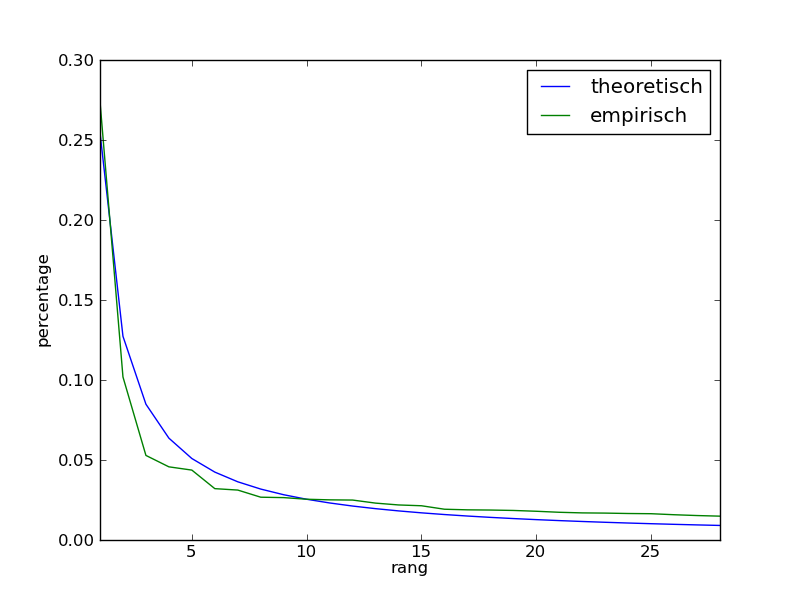
De wet van Zipf¹ is een wetmatigheid die opduikt bij de verdeling van bepaalde getallenreeksen. Bij de analyse van de frequentie van woorden in natuurlijke talen, ontdekte George Kingsley Zipf — naar wie de wet genoemd werd — namelijk dat het meest gebruikte woord ongeveer tweemaal zo vaak voorkomt als het tweede woord, ongeveer driemaal zo vaak als het derde woord, enzovoort. Deze wetmatigheid komt echter niet alleen in de linguïstiek voor. Ondertussen is namelijk gebleken dat een veralgemening van de wet van Zipf ook op een heleboel andere datasets van toepassing is. Zo lijkt de verdeling van een bevolking over de steden in een land tot op een bepaalde hoogte de wet van Zipf te volgen, zoals hieronder geïllustreerd voor het bevolkingsaantal van de 28 grootste steden van Frankrijk.

In zijn algemene vorm kan de wet van Zipf als volgt omschreven worden. Een verdeling volgt de wet van Zipf als het $$n$$-de deel van de verdeling (als die verdeling van groot naar klein is gerangschikt) het percentage $$p(n, \lambda, N)$$ van het totaal bevat. Hierin is $$N$$ het totaal aantal delen in de verdeling en $$\lambda$$ een parameter die in de oorspronkelijke versie van de wet van Zipf gelijk was aan 1. Het percentage $$p(n, \lambda, N)$$ wordt gegeven door onderstaande formule: \[ p(n, \lambda, N) = \frac{1}{\sum_{k=1}^Nk^{-\lambda}}n^{-\lambda} \]

Opgave

1. Schrijf een functie zipf die het theoretisch percentage teruggeeft dat in het $$n$$-de deel van een verdeling in $$N$$ delen zou moeten zitten als de verdeling de wet van Zipf volgt met een parameter $$\lambda$$. De waarden voor $$n$$ en $$N$$ moeten als verplicht argument aan de functie doorgegeven worden en de waarde voor $$\lambda$$ moet als optioneel argument aan de functie worden doorgegeven met een standaardwaarde die gelijk is aan 1.

2. Schrijf een functie leesData waaraan de locatie van een tekstbestand moet doorgegeven worden als eerste verplicht argument. Alle regels van dit tekstbestand moeten eenzelfde aantal informatievelden bevatten, die telkens van elkaar gescheiden worden door één enkel scheidingskarakter. De functie moet als resultaat de lijst van integerwaarden teruggeven, die de waarden uit een gegeven kolom van het tekstbestand bevat. Deze kolom (veldnummers worden geteld vanaf 1) moet als tweede verplicht argument aan de functie doorgegeven worden. Indien het opgegeven veld van het tekstbestand reële getallen bevat, dan moeten deze afgerond worden naar de dichtstbijzijnde integerwaarde. Optioneel kan een derde argument aan de functie doorgegeven worden: het scheidingskarakter dat gebruikt wordt om de informatievelden in het tekstbestand van elkaar te scheiden. Gebruik een tab als standaardwaarde voor dit optioneel argument.

3. Schrijf een functie testZipf die kan gebruikt worden om na te gaan of een gegeven lijst van integerwaarden (die als argument aan de functie doorgegeven wordt) voldoet aan de wet van Zipf met een bepaalde parameter $$\lambda$$ (die als optioneel argument met naam l en standaardwaarde 1 aan de functie doorgegeven wordt). Voor elk $$n$$-de deel in de lijst moet de functie op een afzonderlijk regel eerst het nummer $$n$$ zelf uitschrijven (rechts uitgelijnd over het maximaal aantal posities nodig om de lengte van de lijst uit te schrijven), gevolgd door het aantal in het $$n$$-de deel (rechts uitgelijnd over 6 posities), het theoretische percentage $$p(n, \lambda, N)$$ en het percentage van het $$n$$-de deel in de gegeven lijst. Beide percentages worden telkens rechts uitgelijnd over 10 posities, en worden weergegeven afgerond tot op vier cijfers na de komma.

Voorbeeld

Onderstaande interactieve Pythonsessie maakt gebruik van het bestand frankrijk.txt². Dit is een tekstbestand dat bestaat uit twee kolommen (van elkaar gescheiden door een tab): i) de naam en ii) het aantal inwoners (per duizend) van een stad in Frankrijk.

>>> zipf(1, 28)
0.25463622288862675
>>> zipf(2, 28, 3)
0.1040416849914885

>>> steden = leesData('frankrijk.txt', 2)
>>> steden
[124, 132, 141, 210, ..., 359, 130, 117]

>>> testZipf(steden)
 1  2152    0.2546    0.2741
 2   800    0.1273    0.1019
 3   415    0.0849    0.0529
 4   359    0.0637    0.0457
 5   343    0.0509    0.0437
 6   252    0.0424    0.0321
 7   245    0.0364    0.0312
 8   210    0.0318    0.0267
 9   208    0.0283    0.0265
10   200    0.0255    0.0255
11   197    0.0231    0.0251
12   196    0.0212    0.0250
13   181    0.0196    0.0231
14   172    0.0182    0.0219
15   168    0.0170    0.0214
16   151    0.0159    0.0192
17   148    0.0150    0.0189
18   147    0.0141    0.0187
19   145    0.0134    0.0185
20   141    0.0127    0.0180
21   136    0.0121    0.0173
22   133    0.0116    0.0169
23   132    0.0111    0.0168
24   130    0.0106    0.0166
25   129    0.0102    0.0164
26   124    0.0098    0.0158
27   120    0.0094    0.0153
28   117    0.0091    0.0149

Voorbeeld

Onderstaande interactieve Pythonsessie maakt gebruik van het bestand belgie.txt³. Dit is een tekstbestand dat bestaat uit drie kolommen (van elkaar gescheiden door een komma): i) de naam van een stad in België, ii) het aantal inwoners (per duizend) van die stad en iii) het aantal inwoners (per duizend) van de corresponderende agglomeratie.

>>> belgie_steden = leesData('belgie.txt', 2, ',')
>>> print(belgie_steden)
[470, 92, 117, 136, 207, 231, 76, 197, 104]
>>> testZipf(belgie_steden, 0.77)
1   470    0.2849    0.2883
2   231    0.1671    0.1417
3   207    0.1223    0.1270
4   197    0.0980    0.1209
5   136    0.0825    0.0834
6   117    0.0717    0.0718
7   104    0.0637    0.0638
8    92    0.0575    0.0564
9    76    0.0525    0.0466
>>> belgie_agglom = leesData('belgie.txt', 3, ',')
>>> print(belgie_agglom)
[668, 175, 117, 960, 295, 251, 114, 485, 104]
>>> testZipf(belgiebelgie_agglom, l=0.84)
1   960    0.3052    0.3029
2   668    0.1705    0.2108
3   485    0.1213    0.1530
4   295    0.0953    0.0931
5   251    0.0790    0.0792
6   175    0.0678    0.0552
7   117    0.0595    0.0369
8   114    0.0532    0.0360
9   104    0.0482    0.0328