Bij een klasopdracht krijgen de leerlingen een reeks met $$n$$ verschillende getallen en een reeks met $$n$$ vakjes. Tussen twee opeenvolgende vakjes staat er telkens één ongelijkheidsteken: kleiner dan (<) of groter dan (>). Dat zijn in totaal dus $$n - 1$$ ongelijkheidstekens. De opdracht bestaat erin om de getallen in de vakjes te plaatsen, zodat alle ongelijkheden tussen elke twee opeenvolgende getallen voldaan zijn.

Voor deze opdracht krijg je een reeks met $$n$$ verschillende getallen en een reeks met $$n$$ vakjes. Tussen twee opeenvolgende vakjes staat er telkens één ongelijkheidsteken: kleiner dan (<) of groter dan (>). Dat zijn in totaal dus $$n - 1$$ ongelijkheidstekens. De opdracht bestaat erin om de getallen in de vakjes te plaatsen, zodat alle ongelijkheden tussen elke twee opeenvolgende getallen voldaan zijn.

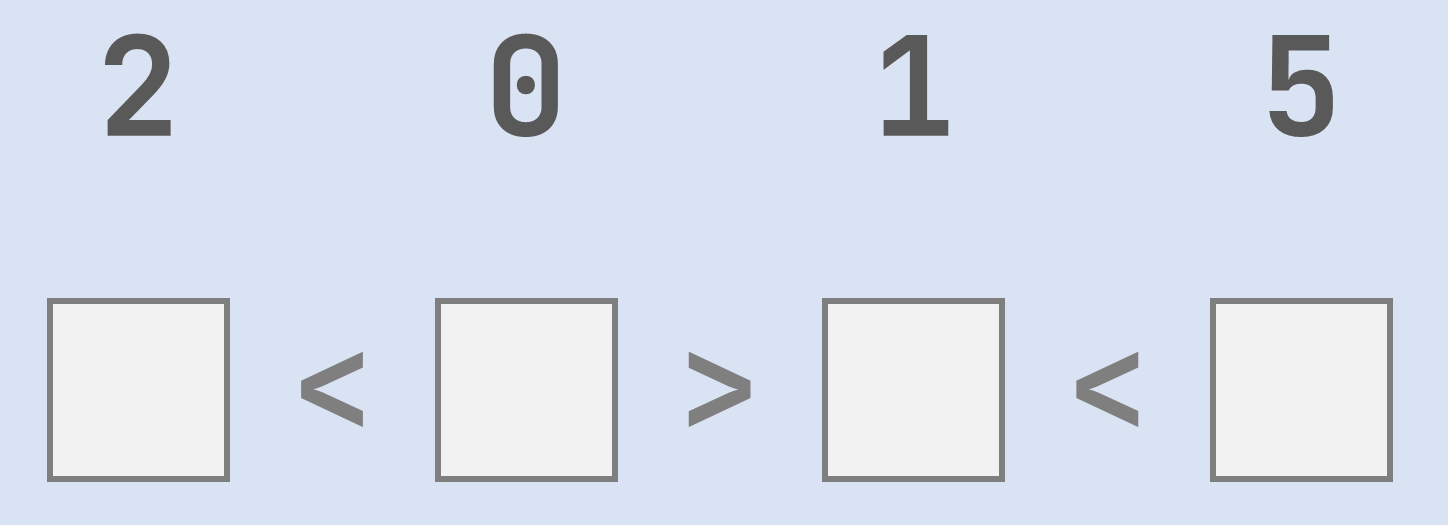
Zomaar de getallen in de gegeven volgorde in de vakjes plaatsen zal niet altijd een correct resultaat opleveren. Als we dat bijvoorbeeld doen voor bovenstaande voorbeeldopgave, dan is de eerste ongelijkheid niet voldaan, maar de twee andere wel.

Als we de getallen in de gegeven volgorde in de vakjes plaatsen, dan krijgen we geen correct resultaat. De eerste ongelijkheid niet correct, maar de twee andere wel.

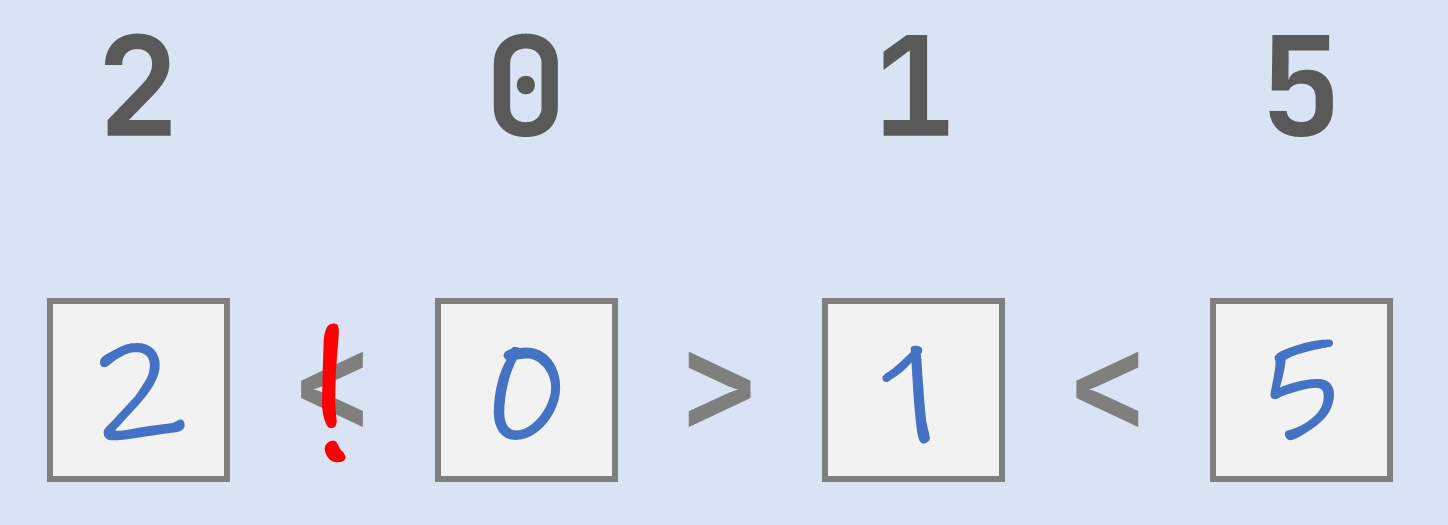
Er bestaat wel een eenvoudig trucje om de gegeven getallen op een correcte manier in de vakjes in te vullen. Eerst rangschikken we de getallen van klein naar groot. Daarna lopen we de ongelijkheidstekens van links naar rechts af. Als we een "kleiner dan"-teken (<) tegenkomen, dan plaatsen we het eerste (kleinste) getal van de rangschikking in het vakje voor het ongelijkheidsteken. Anders plaatsen we het laatste (grootste) getal van de rangschikking in dat vakje. Het getal dat we op deze manier in het vakje geplaatst hebben, wordt uit de rangschikking geschrapt. Nadat we alle ongelijkheidstekens afgelopen hebben, plaatsen we het enige overblijvende getal uit de rangschikking in het laatste vakje (aan de rechterkant).

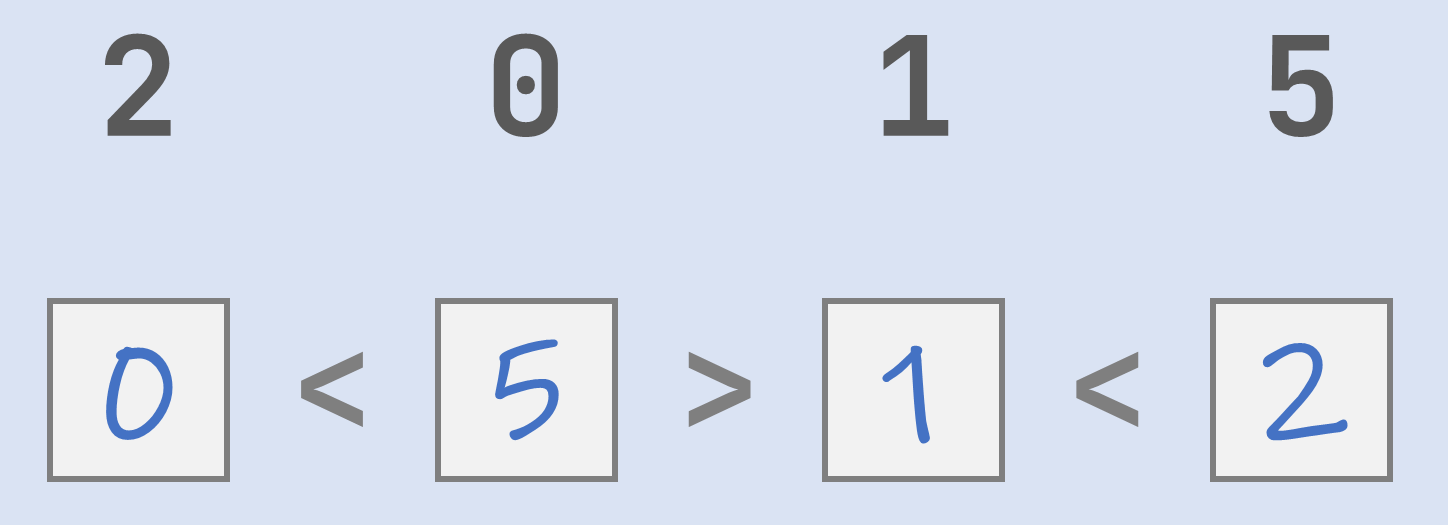
Als we dit trucje toepassen op de voorbeeldopgave, dan rangschikken we eerst de getallen van klein naar groot: 0 1 2 5. Als we de ongelijkheidstekens van links naar rechts aflopen, dan komen we eerst een "kleiner dan"-teken (<) tegen. Daarom schrappen we de 0 aan de voorkant van de rangschikking en plaatsen die in het eerste vakje. De rangschikking die overblijft is dan 1 2 5. Daarna komen we een "groter dan"-teken (>) tegen en dus plaatsen we de 5 achteraan de rangschikking in het tweede vakje. We schrappen ook de 5 uit de rangschikking waardoor we nog 1 2 overhouden. Het laatste ongelijkheidsteken dat we tegenkomen is een "kleiner dan"-teken (<), waardoor we de 1 aan het begin van de rangschikking schrappen en in het derde vakje plaatsen. Dan blijft er enkel nog een 2 over in de rangschikking, en die plaatsen we in het laatste vakje. Het resultaat is een reeks ongelijkheden die allemaal voldaan zijn:

Om een correcte plaatsing te vinden, kunnen we eerst de getallen van klein naar groot rangschikken: 0 1 2 5. Als we de ongelijkheidstekens van links naar rechts aflopen, dan komen we eerst een kleiner dan (<) tegen. Daarom schrappen we de 0 aan de voorkant van de rangschikking en plaatsen die in het eerste vakje. De rangschikking die overblijft is dan 1 2 5. Daarna komen we een groter dan (>) tegen en dus plaatsen we de 5 achteraan de rangschikking in het tweede vakje. We schrappen ook de 5 uit de rangschikking waardoor we nog 1 2 overhouden. De laatste ongelijkheid die we tegenkomen is een kleiner dan (<), waardoor we de 1 aan het begin van de rangschikking schrappen en in het derde vakje plaatsen. Dan blijft er enkel nog een 2 over in de rangschikking, en die plaatsen we in het laatste vakje. Het resultaat is een reeks ongelijkheden die allemaal voldaan zijn.

Nu zou het geen typische klasopdracht zijn, als er ook niet ergens een leerling tussen zat die de opdracht niet goed gehoord of gelezen heeft. Hieronder heeft een leerling bijvoorbeeld de getallen in hun oorspronkelijke volgorde laten staan, maar de gegeven ongelijkheidstekens herschikt.

In dit geval heeft een leerling de getallen in hun oorspronkelijke volgorde laten staan, maar de gegeven ongelijkheidstekens herschikt. Dit levert ook een reeks ongelijkheden op die allemaal voldaan zijn, maar het was natuurlijk niet de bedoeling om de opdracht op deze manier op te lossen. Bovendien is het ook niet altijd mogelijk om de gegeven ongelijkheidstekens te herschikken zodat alle ongelijkheden voldaan zijn.

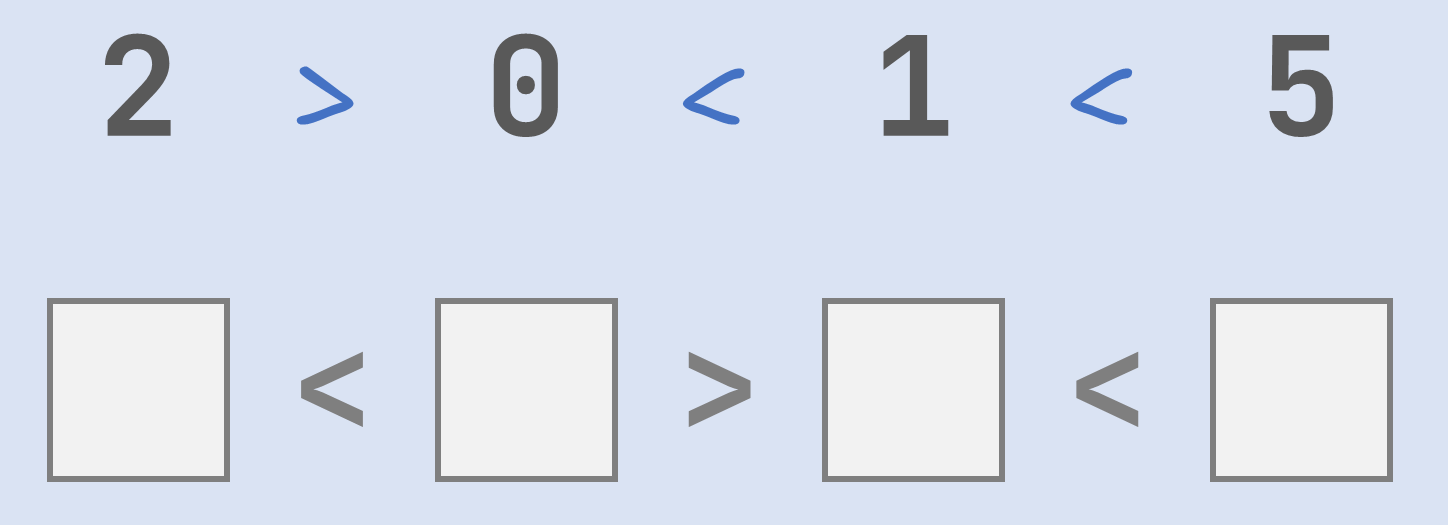
Dit levert ook een reeks ongelijkheden op die allemaal voldaan zijn, maar het was natuurlijk niet de bedoeling om de opdracht op deze manier op te lossen. Bovendien is het ook niet altijd mogelijk om de gegeven ongelijkheidstekens te herschikken zodat alle ongelijkheden voldaan zijn.

Opgave

Voor een opdracht zoals uit de inleiding stellen we de gegeven getallen voor als een lijst (list) met $$n$$ getallen (int). De gegeven ongelijkheidstekens van de opdracht stellen we voor als een string (str) met $$n - 1$$ ongelijkheidstekens: kleiner dan (<) of groter dan (>). Een mogelijke oplossing voor de opdracht wordt ook voorgesteld als een lijst (list) met $$n$$ getallen (int). Gevraagd wordt:

Schrijf een functie isvoldaan waaraan drie argumenten moeten doorgegeven worden: i) een getal $$a$$ (int), ii) een ongelijkheidsteken $$ \otimes $$ (str): kleiner dan (<) of groter dan (>), en iii) een getal $$b$$. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of de ongelijkheid $$a \otimes b$$ voldaan is.
Schrijf een functie correcte_tekens waaraan de getallen van een opdracht moeten doorgegeven worden. De functie moet de ongelijkheidstekens teruggeven die tussen de getallen moeten geplaatst worden, zodat alle ongelijkheden tussen elke twee opeenvolgende getallen voldaan zijn.
Schrijf een functie iscorrect waaraan de getallen en de ongelijkheidstekens van een opdracht moeten doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of de getallen in hun gegeven volgorde in de vakjes invullen een correcte oplossing van de opdracht oplevert.
Schrijf een functie plaats_getallen waaraan de getallen en de ongelijkheidstekens van een opdracht moeten doorgegeven worden. De functie moet de correcte oplossing van de opdracht teruggeven die men bekomt door het trucje uit de inleiding toe te passen om de getallen in de vakjes te plaatsen.
Schrijf een functie plaats_tekens waaraan de getallen en de ongelijkheidstekens van een opdracht moeten doorgegeven worden. De functie moet de herschikking van de ongelijkheidstekens teruggeven die zorgt dat alle ongelijkheden tussen elke twee opeenvolgende getallen voldaan zijn, als we de herschikte ongelijkheidstekens één voor één tussen de getallen plaatsen (zonder de volgorde van de getallen te wijzigen). Als een dergelijke herschikking niet bestaat, dan moet er een AssertionError opgeworpen worden met de boodschap onmogelijke plaatsing.
Schrijf een functie beoordeling waaraan een mogelijke oplossing en de ongelijkheidstekens van een opdracht moeten doorgegeven worden. De functie moet een string (str) teruggeven die bestaat uit de getallen van de mogelijke oplossing. Daarbij worden twee getallen telkens van elkaar gescheiden door een spatie, het volgende ongelijkheidsteken en nog een spatie. Voor ongelijkheden die niet voldaan zijn, wordt het ongelijkheidsteken voorafgegaan door een uitroepteken (!): < wordt dus !< en > wordt !>.

Voorbeeld

        >>> isvoldaan(13, '<', 42)
True
>>> isvoldaan(13, '>', 42)
False

>>> correcte_tekens([2, 0, 1, 5])
'><<'
>>> correcte_tekens([0, 5, 1, 2])
'<><'

>>> iscorrect([2, 0, 1, 5], '<><')
False
>>> iscorrect([0, 5, 1, 2], '<><')
True

>>> plaats_getallen([2, 0, 1, 5], '<><')
[0, 5, 1, 2]
>>> plaats_getallen([66, 95, 6, 7, 73, 97, 69, 68, 51, 21, 3, 93, 58, 42, 54, 19], '<>>>>>><>><<><<')
[3, 97, 95, 93, 73, 69, 68, 6, 66, 58, 7, 19, 54, 21, 42, 51]

>>> plaats_tekens([2, 0, 1, 5], '<><')
'><<'
>>> plaats_tekens([66, 95, 6, 7, 73, 97, 69, 68, 51, 21, 3, 93, 58, 42, 54, 19], '<>>>>>><>><<><<')
'<><<<>>>>><>><>'
>>> plaats_tekens([82, 51, 5, 27, 19, 30, 26, 28, 12, 22], '<<>><><<>')
Traceback (most recent call last):
AssertionError: onmogelijke plaatsing

>>> beoordeling([2, 0, 1, 5], '<><')
'2 !< 0 !> 1 < 5'
>>> beoordeling([0, 5, 1, 2], '<><')
'0 < 5 > 1 < 2'
>>> beoordeling([66, 95, 6, 7, 73, 97, 69, 68, 51, 21, 3, 93, 58, 42, 54, 19], '<>>>>>><>><<><<')
'66 < 95 > 6 !> 7 !> 73 !> 97 > 69 > 68 !< 51 > 21 > 3 < 93 !< 58 > 42 < 54 !< 19'
>>> beoordeling([3, 97, 95, 93, 73, 69, 68, 6, 66, 58, 7, 19, 54, 21, 42, 51], '<>>>>>><>><<><<')
'3 < 97 > 95 > 93 > 73 > 69 > 68 > 6 < 66 > 58 > 7 < 19 < 54 > 21 < 42 < 51'

Opgave

Voorbeeld

Epiloog