Twee doorschijnende stoffen worden van elkaar gescheiden door een vlak scheidingsvlak. Een lichtstraal valt vanaf de ene stof in op dit scheidingsvlak. De hoek die deze lichtstraal maakt met de normaal op dit scheidingsvlak noemen we $$\theta_1$$ met $$0 \le \theta_1 \lt \frac{\pi}{2}$$. Aan dit grensvlak wordt deze straal gebroken, en propageert vanaf dan in de andere stof. De hoek die de gebroken straal met de normaal maakt, noemen we $$\theta_2$$, met opnieuw $$0 \le \theta_2 \lt \frac{\pi}{2}$$.

Breking van een lichtstraal.

Goudmijn: naburen/div>

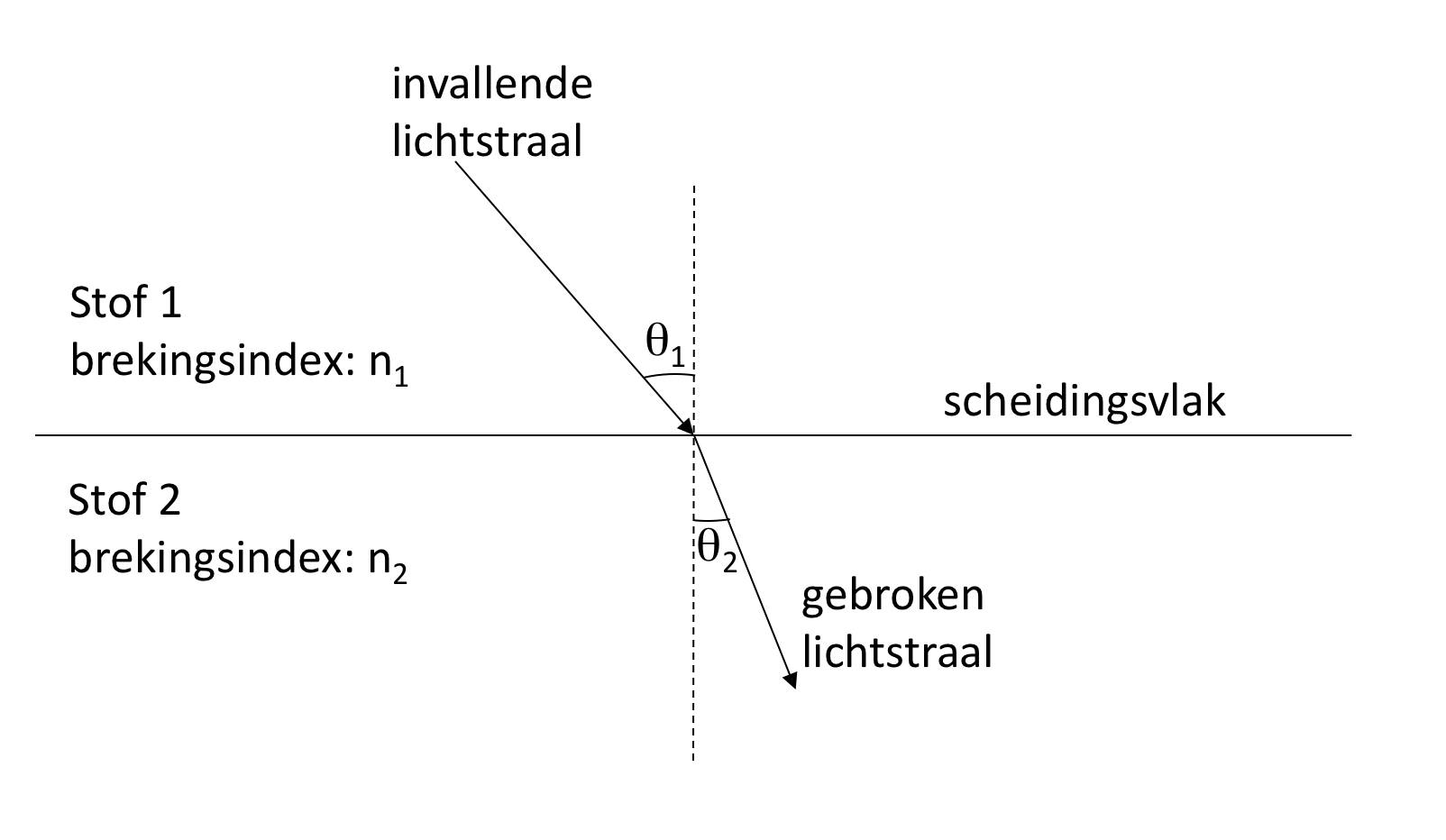
Er geldt bovendien: $$ n_1 \sin{\theta_1} = n_2 \sin{\theta_2} $$

waarin:

$$\theta_1$$ de hoek die de invallende straal maakt met de normaal op het scheidingsvlak
$$\theta_2$$ de hoek die de gebroken straal maakt met de normaal op het scheidingsvlak
$$n_1$$ de brekingsindex van stof 1 (een strikt positieve constante)
$$n_2$$ de brekingsindex van stof 2 (een strikt positieve constante)

Programmeer de functie gebroken_straal() met 3 reële argumenten, achtereenvolgens:

de hoek $$\theta_1$$ (in radiaal)
de brekingsindex $$n_1$$
de brekingsindex $$n_2$$

Het resultaat van de functie is de waarde voor $$\theta_2$$ (in radiaal), waarbij je mag aannemen dat er steeds een gebroken straal bestaat (m.a.w. $$\sin{\theta_2} \le 1$$)

Voorbeeld

gebroken_straal(0.1, 1.3, 1.5) = 0.08663061225286749

Merk op dat je resultaat in de Donona-evaluatie automatisch afgekapt wordt op 6 decimalen (dit gebeurt door de functie prec() in het Dodona verbeterscript).