Onderstaande oneindige som werd door de Griekse wiskundige Archimedes in 200 voor Christus reeds bestudeerd.

\[\mathsf{\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{1}{64}+\dfrac{1}{256}+\ldots }\]

Archimedes wist dat het resultaat van deze som exact gelijk was aan één derde. Dit kan je meetkundig zelfs vrij eenvoudig bewijzen. In onderstaande figuur merk je dat de oppervlaktes van de vierkanten opeenvolgend één vierde, één zestiende, enz.. zijn. Deze oppervlakten drie keer optellen levert het volledige vierkant.

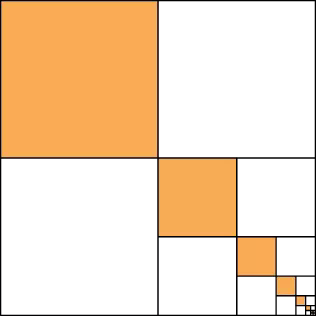
Opgave

Schrijf een programma dat naar het aantal termen vraagt en vervolgens via een begrensde herhaling de partieelsom uitrekent die hiermee overeenkomt. Rond de partieelsom af op 9 cijfers na de komma.

Voorbeelden

Indien de gebruiker 2 intikt, dan wordt de volgende berekening uitgevoerd:

\[\mathsf{\dfrac{1}{4} + \dfrac{1}{16} = 0,3125}\]

Zodat er verschijnt:

Bij 2 termen benadert men de Archimedes reeks als 0.3125

Indien de gebruiker 4 intikt, dan wordt de volgende berekening uitgevoerd:

\[\mathsf{\dfrac{1}{4} + \dfrac{1}{16} +\dfrac{1}{64} +\dfrac{1}{256} \approx 0,332031}\]

Zodat er verschijnt:

Bij 4 termen benadert men de Archimedes reeks als 0.33203125