Het is onmiddellijk duidelijk dat dit geen gewone dobbelstenen zijn, maar wat is er dan wel gewoon aan deze dobbelstenen?

sicherman
De dobbelstenen van Sicherman

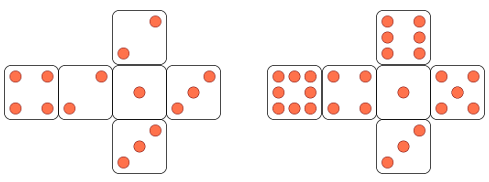
Deze dobbelstenen werden ontdekt door George Sicherman (Buffalo, New York, VSA) en werden voor het eerst gepubliceerd door Martin Gardner in een editie van Scientific American uit 1978. Als de dobbelstenen samen gegooid worden, dan hebben ze dezelfde kansverdeling als een paar gewone dobbelstenen. Er zijn bijvoorbeeld zes manieren om een 7 te gooien, vijf manieren om een 8 te gooien, enzoverder. De dobbelstenen van Sicherman vormen bovendien de enige mogelijke alternatieve schikking van strikt positieve natuurlijke getallen die dezelfde kansverdeling geven als gewone dobbelstenen.

Het is een basisoefening uit de combinatoriek om het aantal mogelijke manieren te bepalen waarop een gegeven waarde kan gegooid worden met een paar gewone zeszijdige dobbelstenen (door de som van het aantal ogen op beide dobbelstenen te nemen). Onderstaande tabel toont het aantal mogelijke manieren voor elke mogelijke uitkomst $$n$$:

$$n$$ 2 3 4 5 6 7 8 9 10 11 12
# manieren 1 2 3 4 5 6 5 4 3 2 1

De vraag die zich stelt is of de ogen op de dobbelstenen ook op een andere manier kunnen geschikt worden zodat de mogelijke uitkomsten van de dobbelstenen dezelfde kansverdeling opleveren. Het verrassende antwoord op deze vraag is dat er inderdaad een mogelijkheid bestaat, onder de vorm van de dobbelstenen van Sicherman. Indien het toegelaten is om dobbelstenen te maken met zijden die geen ogen hebben, dan zijn er nog drie bijkomende combinaties van dobbelstenen met dezelfde kansverdeling mogelijk.

Onderstaande tabel toont alle mogelijke uitkomsten die kunnen bekomen worden met een paar gewone dobbelstenen en met de dobbelstenen van Sicherman. Voor de duidelijk hebben we één van de dobbelstenen van Sicherman gekleurd 1–2–2–3–2–4 en hebben we de andere zwart gelaten 1–3–4–5–6–8.


2 3 4 5 6 7 8 9 10 11 12
gewone dobbelstenen 1+1 1+2
2+1		 1+3
2+2
3+1		 1+4
2+3
3+2
4+1		 1+5
2+4
3+3
4+2
5+1		 1+6
2+5
3+4
4+3
5+2
6+1		 2+6
3+5
4+4
5+3
6+2		 3+6
4+5
5+4
6+3		 4+6
5+5
6+4		 5+6
6+5		 6+6
dobbelstenen van Sicherman 1+1 2+1
2+1		 3+1
3+1
1+3		 1+4
2+3
2+3
4+1		 1+5
2+4
2+4
3+3
3+3		 1+6
2+5
2+5
3+4
3+4
4+3		 2+6
2+6
3+5
3+5
4+4		 1+8
3+6
3+6
4+5		 2+8
2+8
4+6		 3+8
3+8		 4+8

Opgave

In deze opgave stellen we een worp met twee dobbelstenen voor als tuple $$(x, y)$$ waarbij $$x \in \mathbb{N}$$ het aantal ogen voorstelt op de bovenste zijde van de eerste dobbelsteen, en $$y \in \mathbb{N}$$ het aantal ogen op de bovenste zijde van de tweede dobbelsteen. Een dobbelsteen wordt voorgesteld als een collectie (een lijst, tuple, verzameling, …) van natuurlijke getallen. Merk dus op dat we ons in deze opgave niet beperken tot zeszijdige dobbelstenen, en dat het mogelijk is dat sommige zijden van eenzelfde dobbelsteen eenzelfde aantal ogen hebben. Een paar dobbelstenen wordt voorgesteld als een lijst of een tuple van twee dobbelstenen. Gevraagd wordt:

Voorbeeld

>>> dobbel6_1 = {1, 2, 3, 4, 5, 6}
>>> dobbel6_2 = [1, 2, 2, 3, 3, 4]
>>> dobbel6_3 = (1, 3, 4, 5, 6, 8)

>>> worp = combinaties(dobbel6_1, dobbel6_1)
>>> worp[8]
[(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)]
>>> worp = combinaties(dobbel6_2, dobbel6_3)
>>> worp[8]
[(2, 6), (2, 6), (3, 5), (3, 5), (4, 4)]

>>> verdeling(dobbel6_1, dobbel6_1)
{2: 1, 3: 2, 4: 3, 5: 4, 6: 5, 7: 6, 8: 5, 9: 4, 10: 3, 11: 2, 12: 1}
>>> verdeling(dobbel6_2, dobbel6_3)
{2: 1, 3: 2, 4: 3, 5: 4, 6: 5, 7: 6, 8: 5, 9: 4, 10: 3, 11: 2, 12: 1}

>>> gelijkeVerdeling([dobbel6_1, dobbel6_1], (dobbel6_2, dobbel6_3))
True

>>> dobbel8_1 = {1, 2, 3, 4, 5, 6, 7, 8}
>>> dobbel8_2 = (1, 3, 5, 5, 7, 7, 9, 11)
>>> dobbel8_3 = (1, 2, 2, 3, 3, 4, 4, 5)
>>> dobbel8_4 = (1, 2, 5, 5, 6, 6, 9, 10)
>>> dobbel8_5 = (1, 2, 3, 3, 4, 4, 5, 6)

>>> gelijkeVerdeling((dobbel8_1, dobbel8_1), (dobbel8_2, dobbel8_3))
True
>>> gelijkeVerdeling((dobbel8_1, dobbel8_1), (dobbel8_3, dobbel8_4))
False
>>> gelijkeVerdeling((dobbel8_1, dobbel8_1), (dobbel8_4, dobbel8_5))
True

Bronnen