Leonardo Barichello bedacht dit gedachte-experiment over waarschijnlijkheid: twee mensen zijn gestrand op een onbewoond eiland met slechts één banaan om te eten. Om te beslissen wie de banaan mag opeten, gaan ze akkoord om een spel te spelen. Ze zullen elk met een eerlijke 6-zijdige dobbelsteen gooien. Als het hoogste aantal ogen dat door de twee spelers gegooid werd 1, 2, 3 of 4 is, dan mag speler 1 de banaan opeten. Als het hoogste aantal ogen dat door de twee spelers gegooid werd 5 of 6 is, dan mag speler 2 de banaan opeten. Welke speler heeft het meest kans om de banaan te mogen opeten?
Misschien ietwat verrassend, maar speler 2 heeft het meest kans om de banaan te mogen opeten. Onderstaande tabel bevat de 36 mogelijke uitkomsten van twee worpen met een 6-zijdige dobbelsteen. Met een eerlijke dobbelsteen hebben elk van deze 36 uitkomsten evenveel kans om geworpen te worden. Daarvan zijn er 16 waarbij speler 1 wint (44.4%, aangegeven in het groen) en 20 waarbij speler 2 wint (55.6%, aangegeven in het blauw).
| worp1 | worp2 | winnaar |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 2 |
| 1 | 6 | 2 |
| 2 | 1 | 1 |
| 2 | 2 | 1 |
| 2 | 3 | 1 |
| worp1 | worp2 | winnaar |
|---|---|---|
| 2 | 4 | 1 |
| 2 | 5 | 2 |
| 2 | 6 | 2 |
| 3 | 1 | 1 |
| 3 | 2 | 1 |
| 3 | 3 | 1 |
| 3 | 4 | 1 |
| 3 | 5 | 2 |
| 3 | 6 | 2 |
| worp1 | worp2 | winnaar |
|---|---|---|
| 4 | 1 | 1 |
| 4 | 2 | 1 |
| 4 | 3 | 1 |
| 4 | 4 | 1 |
| 4 | 5 | 2 |
| 4 | 6 | 2 |
| 5 | 1 | 2 |
| 5 | 2 | 2 |
| 5 | 3 | 2 |
| worp1 | worp2 | winnaar |
|---|---|---|
| 5 | 4 | 2 |
| 5 | 5 | 2 |
| 5 | 6 | 2 |
| 6 | 1 | 2 |
| 6 | 2 | 2 |
| 6 | 3 | 2 |
| 6 | 4 | 2 |
| 6 | 5 | 2 |
| 6 | 6 | 2 |
Opgave
In een uitbreiding op dit gedachte-experiment gooien de twee spelers met een eerlijke dobbelsteen met $$n \in \mathbb{N}$$ zijden ($$n \geq 4$$). De zijden zijn gemarkeerd met 1 tot en met $$n$$ ogen. De uitkomst van een worp met deze dobbelsteen wordt voorgesteld door een natuurlijk getal (int) tussen 1 en $$n$$.

Speler 1 wint het spel als de worp van beide spelers kleiner of gelijk is aan een bovengrens $$b \in \mathbb{N}$$ ($$1 \leq b \leq n$$) die op voorhand vastgelegd is. Anders wint speler 2. Gevraagd wordt:
-
Schrijf een functie heeft_gewonnen waaraan drie argumenten moeten doorgegeven worden: i) de uitkomst (int) van een worp met de dobbelsteen door speler 1, ii) de uitkomst (int) van de worp met de dobbelsteen door speler 2 en iii) de bovengrens $$b$$ (int). De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of speler 1 het spel gewonnen heeft.
-
Schrijf een functie winnende_uitkomsten waaraan twee argumenten moeten doorgegeven worden: i) het aantal zijden $$n$$ (int) van de dobbelsteen en ii) de bovengrens $$b$$ (int). De functie moet een tuple met twee getallen (int) teruggeven: i) het aantal mogelijke uitkomsten van twee worpen met de $$n$$-zijdige dobbelsteen waarbij speler 1 wint en ii) het aantal mogelijke uitkomsten van twee worpen met de $$n$$-zijdige dobbelsteen waarbij speler 2 wint.
Tip
Om het aantal winnende uitkomsten van beide spelers te bepalen, kan de functie alle mogelijke uitkomsten van twee worpen met een $$n$$-zijdige dobbelsteen overlopen en voor elke uitkomst bepalen wie er in dat geval wint.
-
Schrijf een functie winstkansen waaraan twee argumenten moeten doorgegeven worden: i) het aantal zijden $$n$$ (int) van de eerlijke dobbelsteen en ii) de bovengrens $$b$$ (int). De functie moet een tuple met twee getallen (float) teruggeven: i) de kans dat speler 1 het spel wint en ii) de kans dat speler 2 het spel wint. Beide kansen moeten uitgedrukt worden als een percentage.
Tip
De procentuele kans dat een speler het spel wint is gelijk aan het aantal mogelijke uitkomsten waarbij de speler het spel wint, gedeeld door het aantal mogelijke uitkomsten, maal 100.
-
Schrijf een functie winnaar waaraan twee argumenten moeten doorgegeven worden: i) het aantal zijden $$n$$ (int) van de eerlijke dobbelsteen en ii) de bovengrens $$b$$ (int). De functie moet een integer (int) teruggeven: de waarde 0 als beide spelers evenveel kans hebben om te winnen, de waarde 1 als speler 1 het meest kans heeft om te winnen, en de waarde 2 als speler 2 het meest kans heeft om te winnen.
Voorbeeld
>>> heeft_gewonnen(3, 2, 4)
True
>>> heeft_gewonnen(1, 5, 4)
False
>>> winnende_uitkomsten(6, 4)
(16, 20)
>>> winstkansen(6, 4)
(44.44444444444444, 55.55555555555556)
>>> winnaar(6, 4)
2
Epiloog
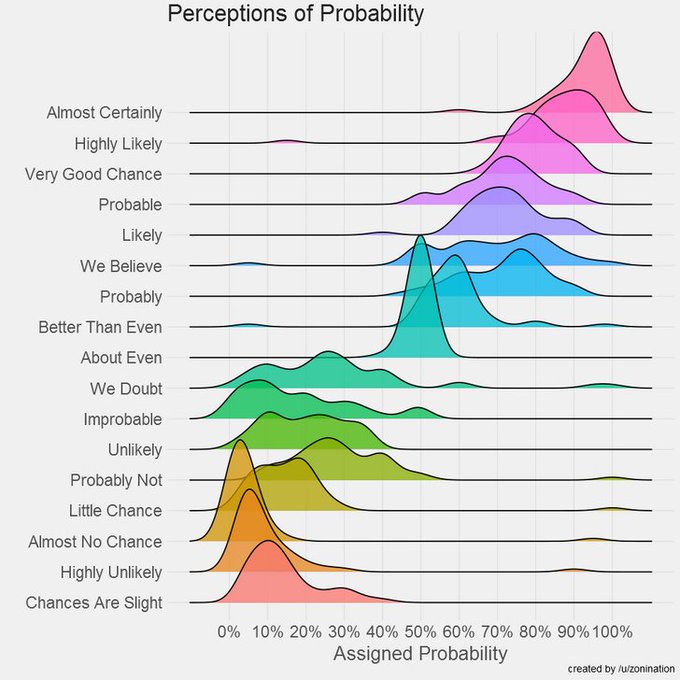
Over welk soort waarschijnlijkheid hebben mensen het als ze zeggen dat iets "bijna geen kans" heeft of "bijna zeker" is? Deze grafiek1 visualiseert de verschillende percepties van waarschijnlijkheid.