Een aanplakbord wordt verdeeld in verticale stroken die allemaal even breed zijn. Op het bord worden achtereenvolgens een aantal verkiezingsposters geplakt. De posters zijn even hoog als het bord zelf, worden op verschillende plaatsen aangebracht, en bedekken daarbij precies een aantal opeenvolgende stroken. De posters zijn evenwel niet allemaal even breed, en worden mogelijks over elkaar heen geplakt. Vraag is hoeveel posters er finaal nog voor minstens een deel zichtbaar zijn.
Veronderstel bijvoorbeeld dat een aanplakbord tien stroken heeft, en dat er achtereenvolgens vijf posters op geplakt worden:
een poster die begint vanaf strook 1 en 4 stroken breed is
een poster die begint vanaf strook 2 en 5 stroken breed is
een poster die begint vanaf strook 8 en 3 stroken breed is
een poster die begint vanaf strook 3 en 2 stroken breed is
een poster die begint vanaf strook 7 en 4 stroken breed is
Uit onderstaande grafische voorstelling van deze situatie blijkt dat er uiteindelijk nog vier van de vijf posters (gedeeltelijk) zichtbaar zijn.
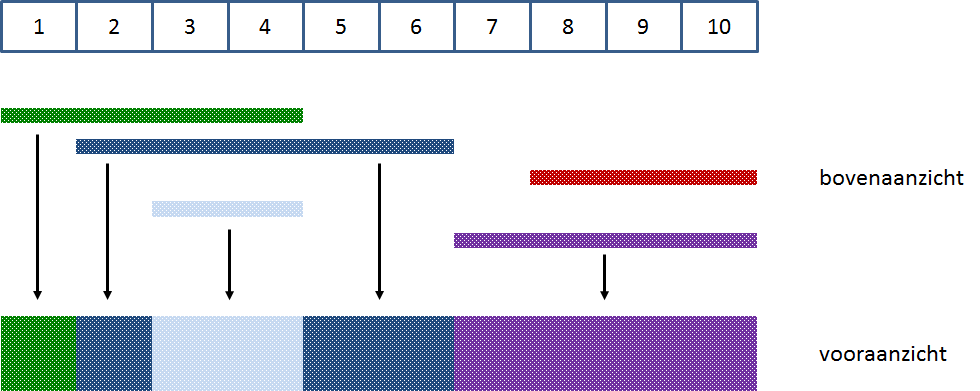
Merk op dat je er niet a priori mag van uitgaan dat aanplakborden altijd onderverdeeld zijn in tien stroken, zoals dat het geval is in bovenstaand voorbeeld.
Opgave
Schrijf een functie zichtbaar waaraan een lijst van tuples moet doorgegeven worden, waarbij elk tuple twee natuurlijke getallen bevat. Deze tuples beschrijven de posities van een aantal posters die in de opgelijste volgorde op een aanplakbord aangebracht worden. Het eerste tuple komt dus overeen met de poster die eerst wordt aangebracht. Het laatste tuple met de poster die als laatste wordt aangebracht. Het eerste getal van een tuple geeft de strook aan waar het linkerdeel van de poster wordt aangebracht, en het tweede getal van een tuple geeft aan hoeveel stroken de poster breed is. De functie moet teruggeven hoeveel posters er uiteindelijk nog (gedeeltelijk) zichtbaar zijn.
Voorbeeld
>>> zichtbaar([(1, 4), (2, 5), (8, 3), (3, 2), (7, 4)])
4
>>> zichtbaar([(3, 5), (1, 4), (5, 6)])
2
>>> zichtbaar([(2, 1), (5, 1)])
2