Nagaan van modelveronderstellingen

Voor de statistische besluitvorming hebben we volgende aannames gedaan

1. Lineariteit
2. Onafhankelijkheid
3. Homoscedasticiteit
4. Normaliteit

Onafhankelijkheid is moeilijk te verifiëren op basis van de data, dat zou gegarandeerd moeten zijn door het design van de studie. Als we afwijkingen zien van lineariteit dan heeft besluitvorming geen zin gezien het de primaire veronderstelling is. In dat geval moeten we het conditioneel gemiddeld eerst beter modelleren. In geval van lineariteit maar schendingen van homoscedasticiteit of normaliteit dan weten we dat de besluitvorming mogelijks incorrect is omdat de teststatistiek dan niet langer een t-verdeling volgt.

Lineariteit

De primaire veronderstelling in lineaire regressie-analyse is de aanname dat de uitkomst (afhankelijke variabele) lineair varieert ten opzichte van de verklarende variabele. Deze veronderstelling kan men gemakkelijk grafisch verifiëren op basis van een scatterplot waarbij men de uitkomst uitzet in functie van de verklarende variabele. Vervolgens gaat men na of het verband een lineair patroon volgt.
In Figuur 28 zien we systematische afwijkingen bij kleine en grote waarden voor de ESR1 expressie. De observaties liggen dan steeds systematisch boven de regressierechte wat aangeeft dat het gemiddelde in deze regio’s systematisch wordt onderschat. Afwijkingen van lineariteit worden vaak echter makkelijker opgespoord d.m.v. een residuplot. Dit is een scatterplot met de verklarende variabele op de $X$-as en de residuen op de $Y$-as

deze werden weergegeven in Figuur 29.

Als de veronderstelling van lineariteit opgaat, krijgt men in een residuplot geen patroon te zien. De residuen zijn immers gemiddeld nul voor elke waarde van de predictor en zouden dus mooi rond nul moeten variëren.

Wanneer de residu’s echter een niet-lineair patroon onthullen, dan geeft dit aan dat extra termen in het model moeten worden opgenomen om de gemiddelde uitkomst correct te voorspellen. Bijvoorbeeld, wanneer de residu’s een kwadratisch patroon onthullen, dan kunnen we schrijven dat bij benadering $e_i\approx {\delta }_0+{\delta }_1{x}_i+{\delta }_2{x}_i^2$ voor zekere getallen ${\delta }_0,{\delta }_1,{\delta }_2$, en bijgevolg dat de uitkomst $y_i=\hat{\alpha }+\hat{\beta }{x}_i+e_i\approx (\hat{\alpha }+{\delta }_0)+(\hat{\beta }+{\delta }_1)x_i+{\delta }_2{x}_i^2$ (op een foutterm na) een kwadratische functie is van $x_i$. In dat geval is het aangewezen om op een kwadratisch regressiemodel over te stappen (zie Hoofdstuk 10). Residuplots worden standaard gegenereerd door de R-software. Hier worden de residuen echter geplot ten opzichte van de gefitte waarden wat eenvoudiger is wanneer meerdere predictoren in het model worden opgenomen (zie Hoofdstuk 10).

                
            par(mfrow=c(2,2))
plot(lm1)

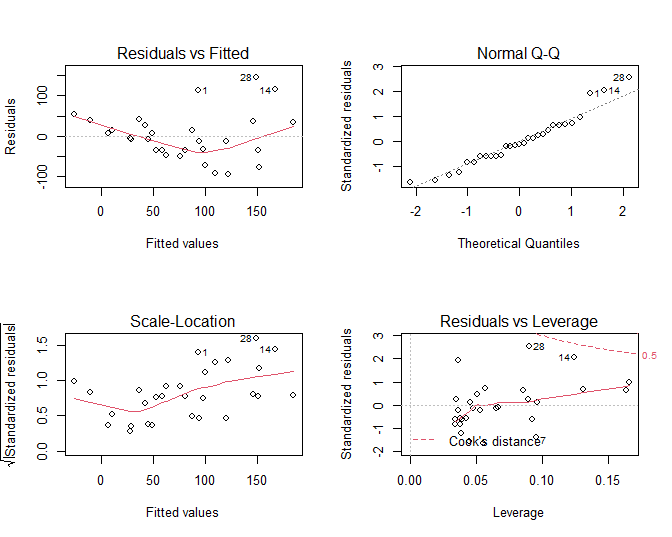
Figuur 30: Diagnostische plots voor het nagaan van de veronderstellingen van het lineair regressiemodel waarbij de S100A8 expressie wordt gemodelleerd i.f.v de ESR1 expressie (na verwijdering van 3 outliers).

De residu plot voor het borstkanker voorbeeld wordt weergegeven in Figuur 30 boven links. De residuen zijn niet overal mooi gespreid rond nul. Bij lage en hoge voorspelde waarden voor het model (dus bij hoge en lage waarden voor de predictor, negatieve helling) zijn de residuen overwegend positief wat opnieuw aangeeft dat het model de data in deze regio’s systematisch onderschat. Dat was ergens te verwachten gezien de smoother in Figuur 27 immers eerder een exponentiëel verband suggereerde. Bovendien voorspelde het regressiemodel eveneens negatieve waarden voor de S100A8 expressie wat onmogelijk is voor intensiteitsmetingen die immers steeds positief zijn.

Veronderstelling van homoscedasticiteit (gelijkheid van variantie)

Residuen en kwadratische residu’s dragen informatie in zich over residuele variabiliteit. Als er homoscedasiticiteit is dan verwachten we dat de residuen eenzelfde spreiding hebben voor elke waarde van de predictor en voor elke predictie. Als de spreiding in de residuen geassocieerd zijn met de verklarende variabelen, dan is er indicatie van heteroscedasticiteit. De diagnostische plots van het software pakket R geven een residu-plot weer en een plot van de vierkantswortel van de absolute waarde van de gestandardiseerde error $\sqrt{|e_i|/\sqrt{MSE}}$ in functie van de predicties. De residu-plot voor het borstkanker voorbeeld Figuur 30 boven links geeft afwijkingen weer van homoscedasiticiteit. De spreiding in de residuen lijkt toe te nemen met een toenemende waarde van de predictor. De plot beneden links is specifiek om de voorwaarde van gelijkheid van variantie na te gaan en geeft eveneens aan dat de variantie toeneemt met het conditioneel gemiddelde. Een dergelijke trend komt dikwijls voor bij concentratiemetingen en intensiteitsmetingen, die vaak een multiplicatieve errorstructuur vertonen i.p.v. een additieve error.

Voor bepaalde types uitkomsten bestaan er variantie-stabiliserende transformaties voor de afhankelijke variabele die erop gericht zijn om de onderstelling van homoscedasticiteit te doen opgaan. Voor proporties of percentages, gebruikt men bijvoorbeeld vaak de arcsin-transformatie die de uitkomst $Y$ omzet in $\arcsin \sqrt{Y}$, omdat men kan aantonen dat percentages (onder bepaalde onderstellingen) een constante variantie hebben na deze transformatie. Voor concentraties en intensiteitsmetingen gebruikt men dan weer vaak een logaritmische transformatie gezien deze (a) positief zijn, (b) vaak gekenmerkt worden door een variantie die toeneemt met het gemiddelde en (c) veelal een scheve verdeling vertonen maar rechts. Indien transformatie van de uitkomst niet helpt of niet wenselijk is (bijvoorbeeld, omdat het de interpretatie van het model niet ten goede komt) en er is een consistent patroon van ongelijke variantie (bijvoorbeeld, toenemende variantie in uitkomst bij toenemende predictorwaarden), dan kan men ook gewogen kleinste kwadratenschatters (in het Engels: weighted least squares) bepalen. Een verder alternatief is om veralgemeende lineaire modellen (in het Engels: generalized linear models) te schatten die tevens andere verdelingen voor de uitkomst dan de Normale verdeling toelaten. Beide klassen van oplossingen (d.i. gewogen kleinste kwadratenschatters en veralgemeende lineaire modellen) vallen echter buiten het bestek van deze cursus.

Veronderstelling van normaliteit

Opnieuw kunnen we de veronderstelling van normaliteit nagaan door gebruik te maken van QQ-plots. Een QQ-plot van de afhankelijke variabele is misleidend omdat deze nagaat of de metingen voor alle subjecten samen Normaal verdeeld zijn. Dat is echter niet het geval gezien de normale verdeling per subject varieert. Elk subject kan immers andere waarde hebben voor de predictor $X$ (ESR1 expressie) en bijgevolg hebben ze een verschillend conditioneel gemiddelde. Normaal verdeelde uitkomsten bij gegeven $x$-waarde impliceert echter dat de residu’s bij benadering Normaal verdeeld zijn. Afwijkingen van Normaliteit in een QQ-plot van de residu’s levert dus een indicatie dat de uitkomsten niet Normaal verdeeld zijn bij vaste $x$.

Figuur 30 rechts boven geeft de QQ-plot weer van de residuen voor het borstkanker voorbeeld. We zien wat afwijkingen in de rechterstaart die wijzen op meerdere outliers of op observaties die systematisch hoger liggen dan wat verwacht kan worden op basis van de normaalverdeling. Dit is niet verrassend omdat heterogeniteit van de variantie vaak samengaat met niet-Normaliteit, i.h.b. scheefheid, van de gegevens. Dat komt vaak voor bij concentratie- en intensiteitsmetingen.