Vier punten in het vlak vormen een vierkant als en slechts als de vier zijden even lang zijn én de twee diagonalen even lang zijn.

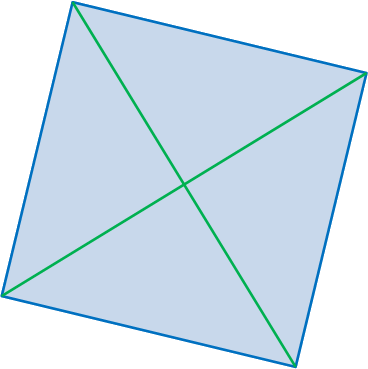
De volgende reeksen van vier punten vormen dus telkens een vierkant:

(0,0), (0,1), (1,1), (1,0)
(0,0), (1,1), (0,1), (1,0)
(0,0), (2,1), (3,-1), (1, -2)

Let dus op het feit dat de punten in een willekeurige volgorde kunnen opgegeven worden, en dat de zijden van het vierkant niet noodzakelijk evenwijdig moeten zijn met de $$X$$- en $$Y$$-as. De volgende reeksen van vier punten vormen geen vierkant, maar respectievelijk een rechthoek, een ruit en een ontaard geval:

(0,0), (0,2), (3,2), (3,0)
(0,0), (3,4), (8,4), (5,0)
(0,0), (0,0), (1,1), (0,0)

Invoer

Acht reële getallen die elk op een afzonderlijke regel staan. Deze getallen zijn respectievelijk de $$x$$- en $$y$$-coördinaat van het punt $$a$$, de $$x$$- en $$y$$-coördinaat van het punt $$b$$, de $$x$$- en $$y$$-coördinaat van het punt $$c$$ en de $$x$$- en $$y$$-coördinaat van het punt $$d$$. De vier punten zullen nooit alle vier samenvallen, dus dit geval moet je niet controleren. Wees op je hoede voor het vergelijken van reële getallen! Lees als voorbereiding de sectie in The Python Tutorial¹ over de beperkingen van floating point getallen of bekijk onderstaande video waarin Pythia enkele tips geeft over het werken met floating point getallen.

Uitvoer

Een regel met vierkant als de vier punten een vierkant voorstellen en geen vierkant in het andere geval.

Voorbeeld

Invoer:

0.0
0.0
0.0
1.0
1.0
1.0
1.0
0.0

Uitvoer:

vierkant

Voorbeeld

Invoer:

0.0
0.0
3.0
4.0
8.0
4.0
5.0
0.0

Uitvoer:

geen vierkant