Als we een rij appartementen die naast elkaar staan in vooraanzicht bekijken, dan zien we dat hun aantal verdiepingen varieert. We kunnen de appartementen dus beschrijven door een reeks (list of tuple) van natuurlijke getallen (int) die aangeven hoeveel verdiepingen elk appartement telt (opgelijst van links naar rechts). Op die manier stelt $$[1, 4, 3, 2, 3, 1]$$ de volgende rij van zes appartementen voor.

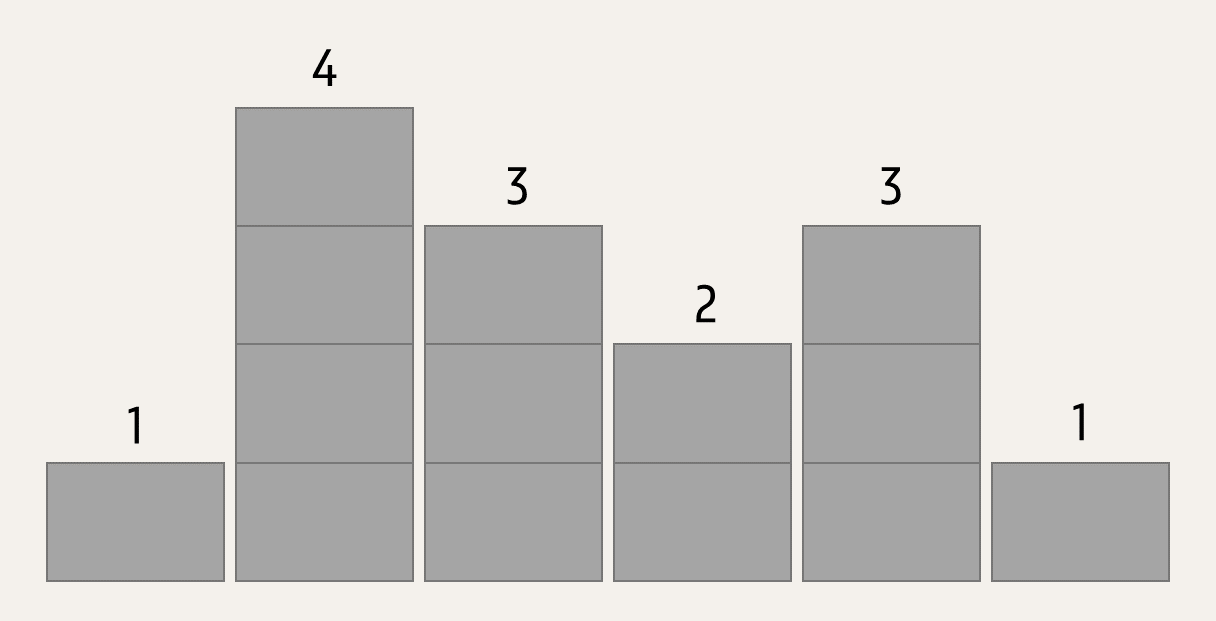
Die appartementen zien er nogal grijs uit en dus besluiten we om ze te schilderen. Per verdieping schilderen we van links naar rechts zoveel mogelijk appartementen met één horizontale penseelstreek in dezelfde kleur. We kiezen telkens een nieuwe kleur als we van verdieping veranderen of als er op een verdieping een gat zit tussen twee appartementen.

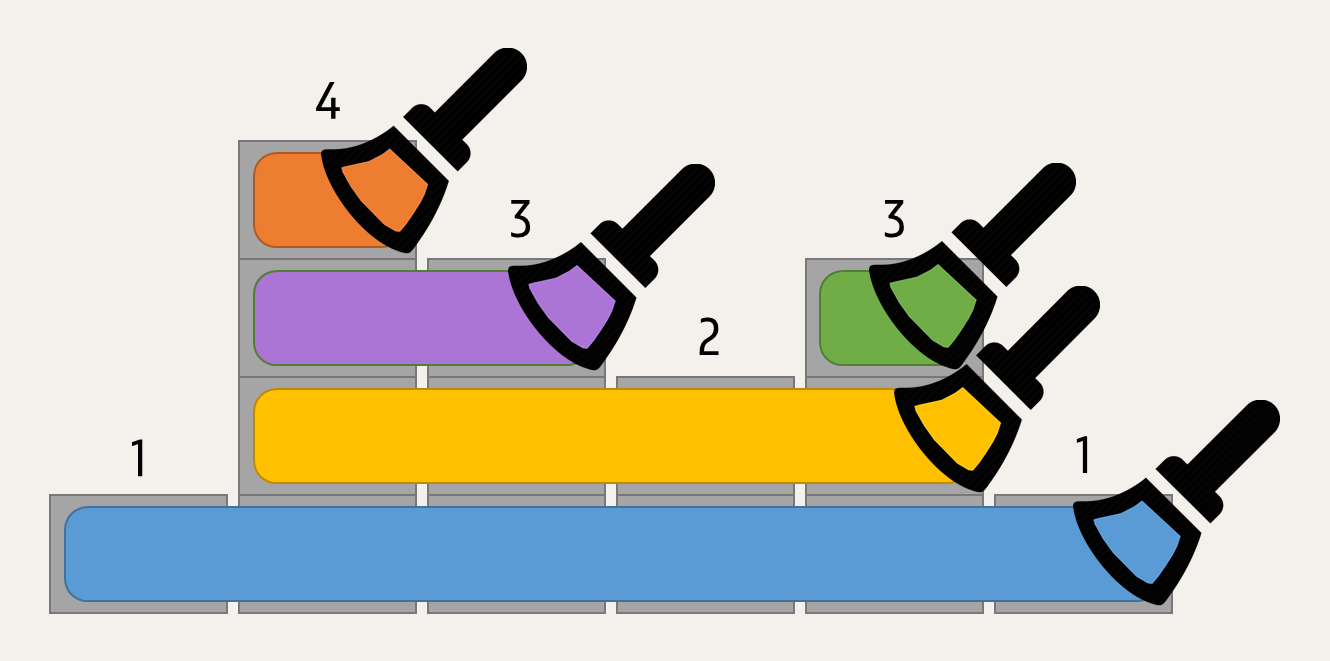
Als we voor de appartementen $$[1, 4, 3, 2, 3, 1]$$ van onder naar boven werken, dan schilderen we met een eerste penseelstreek de onderste verdieping van de zes appartementen in het blauw. Met een tweede penseelstreek schilderen we de tweede verdieping van vier appartementen in het geel. De derde penseelstreek bedekt de derde verdieping van twee appartementen in het paars en met een vierde penseelstreek schilderen we de derde verdieping van nog één appartement in het groen. Ten slotte hebben we nog een vijfde penseelstreek nodig om de vierde verdieping van één appartement in het oranje te zetten. In totaal hebben we dus vijf penseelstreken nodig om alle appartementen in vijf verschillende kleuren te schilderen.

Opgave

We stellen een rij appartementen voor door een reeks (list of tuple) natuurlijke getallen (int) die het aantal verdiepingen van elk appartement aanduiden (opgelijst van links naar rechts). Gevraagd wordt:

• Schrijf een functie verdiepingen waaraan een rij van $$n$$ appartementen moet doorgegeven worden. De functie moet een lijst (list) met $$m$$ verdiepingen teruggeven (opgelijst van boven naar onder), waarbij $$m$$ gelijk is aan het aantal verdiepingen van het hoogste appartement. Elke verdieping wordt zelf voorgesteld door een lijst (list) van $$n$$ Booleaanse waarden (bool) die aangeven of het appartement op de overeenkomstige positie tot aan die verdieping reikt.

• Schrijf een functie vooraanzicht die een voorstelling (str) van het vooraanzicht van een rij appartementen teruggeeft. De voorstelling moet evenveel regels tellen als het aantal verdiepingen van het hoogste appartement. Het exacte formaat van de voorstelling kan uit onderstaand voorbeeld afgeleid worden. De rij van $$n$$ appartementen moet als argument aan de functie doorgegeven worden. Daarnaast heeft de functie ook nog de volgende optionele parameters:

  • breedte (int; standaardwaarde: 3): breedte van één appartement in de voorstelling, uitgedrukt in aantal karakters

  • afstand (int; standaardwaarde: 1): afstand tussen twee appartementen in de voorstelling, uitgedrukt in aantal karakters

  • appartement (str; standaardwaarde: #): één enkel karakter dat gebruikt wordt om appartementen voor te stellen

  • lucht (str; standaardwaarde: spatie): één enkel karakter dat gebruikt wordt om lucht (waar geen appartement staat) voor te stellen

• Schrijf een functie penseelstreken waaraan een rij van $$n$$ appartementen moet doorgegeven worden. De functie moet teruggeven hoeveel penseelstreken (en dus ook hoeveel verschillende kleuren) er nodig zijn om de gegeven reeks appartementen te schilderen volgens de procedure die we hierboven beschreven hebben.

Voorbeeld

>>> appartementen = (1, 4, 3, 2, 3, 1)
>>> verdiepingen(appartementen)
[[False, True, False, False, False, False], [False, True, True, False, True, False], [False, True, True, True, True, False], [True, True, True, True, True, True]]

>>> print(vooraanzicht(appartementen, lucht='~'))
~~~~###~~~~~~~~~~~~~~~~
~~~~###~###~~~~~###~~~~
~~~~###~###~###~###~~~~
###~###~###~###~###~###
>>> print(vooraanzicht(appartementen, breedte=4, afstand=0, appartement='<', lucht="-"))
----<<<<----------------
----<<<<<<<<----<<<<----
----<<<<<<<<<<<<<<<<----
<<<<<<<<<<<<<<<<<<<<<<<<

>>> penseelstreken(appartementen)
5