Introduction to Mendelian inheritance

Modern laws of inheritance were first described by Gregor Mendel¹ (an Augustinian friar) in 1865. The contemporary hereditary model — called blending inheritance — stated that an organism must exhibit a blend of its parent's traits. This rule is obviously violated both empirically (consider the huge number of people who are taller than both their parents) and statistically (over time, blended traits would simply blend into the average, severely limiting variation).

Mendel, working with thousands of pea plants, believed that rather than viewing traits as continuous processes, they should instead be divided into discrete building blocks called factors. Furthermore, he proposed that every factor possesses distinct forms, called alleles.

In what has come to be known as his first law (also known as the law of segregation), Mendel stated that every organism possesses a pair of alleles for a given factor. If an individual's two alleles for a given factor are the same, then it is homozygous for the factor. If the alleles differ, then the individual is heterozygous. The first law concludes that for any factor, an organism randomly passes one of its two alleles to each offspring, so that an individual receives one allele from each parent.

Mendel also believed that any factor corresponds to only two possible alleles, the dominant and recessive alleles. An organism only needs to possess one copy of the dominant allele to display the trait represented by the dominant allele. In other words, the only way that an organism can display a trait encoded by a recessive allele is if the individual is homozygous recessive for that factor.

We may encode the dominant allele of a factor by a capital letter (e.g., $$A$$) and the recessive allele by a lower case letter (e.g., $$a$$). Because a heterozygous organism can possess a recessive allele without displaying the recessive form of the trait, we henceforth define an organism's genotype to be its precise genetic makeup and its phenotype as the physical manifestation of its underlying traits.

The different possibilities describing an individual's inheritance of two alleles from its parents can be represented by a Punnett square.

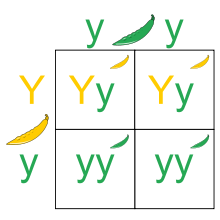
Assignment

Probability is the mathematical study of randomly occurring phenomena. We will model such a phenomenon with a random variable, which is simply a variable that can take a number of different distinct outcomes depending on the result of an underlying random process.

For example, say that we have a bag containing 3 red balls and 2 blue balls. If we let $$X$$ represent the random variable corresponding to the color of a drawn ball, then the probability of each of the two outcomes is given by $$P(X = \textrm{red}) = \frac{3}{5}$$ and $$P(X = \textrm{blue}) = \frac{2}{5}$$.

Random variables can be combined to yield new random variables. Returning to the ball example, let $$Y$$ model the color of a second ball drawn from the bag (without replacing the first ball). The probability of $$Y$$ being red depends on whether the first ball was red or blue. To represent all outcomes of $$X$$ and $$Y$$, we therefore use a probability tree diagram. This branching diagram represents all possible individual probabilities for $$X$$ and $$Y$$, with outcomes at the endpoints ("leaves") of the tree. The probability of any outcome is given by the product of probabilities along the path from the beginning of the tree. See the figure below for an illustrative example.

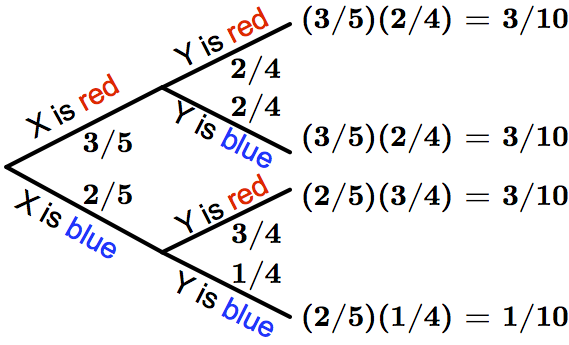
An event is simply a collection of outcomes. Because outcomes are distinct, the probability of an event can be written as the sum of the probabilities of its constituent outcomes. For our colored ball example, let $$A$$ be the event "$$Y$$ is blue". $$P(A)$$ is equal to the sum of the probabilities of two different outcomes: \[P(X = \textrm{blue and }\,Y = \textrm{blue}) + P(X = \textrm{red and }\,Y = \textrm{blue}) = \frac{3}{10} + \frac{1}{10} = \frac{2}{5}\]

Write a function probability that takes three positive integers $$k$$, $$m$$ and $$n$$, representing a population containing $$k + m + n$$ organisms: $$k$$ individuals are homozygous dominant for a factor, $$m$$ are heterozygous, and $$n$$ are homozygous recessive. The function must return the probability that two randomly selected mating organisms will produce an individual possessing a dominant allele (and thus displaying the dominant phenotype). Assume that any two organisms can mate.

Example

>>> probability(2, 2, 2)
0.7833333333333333
>>> probability(30, 24, 17)
0.8354124748490945
>>> probability(18, 19, 18)
0.7530303030303032

Hint

Consider simulating inheritance on a number of small test cases in order to check your solution.