Een onderzoeksgroep traint een neuraal netwerk met heel diepe lagen. Bij het berekenen van de gradiënten (afgeleiden die bepalen hoe het model leert), moeten ze keer op keer een getal kleiner dan 1 vermenigvuldigen.

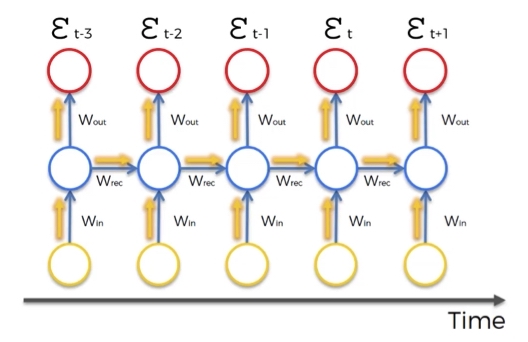
Stel dat bij elke laag een factor van 0,000002 wordt vermenigvuldigd.

• Zonder logaritmen

Bereken de waarde van \((0.000002)^{20}\) met je rekentoestel. Je zal zien dat de rechtstreekse vermenigvuldiging van extreem kleine waarden snel leidt tot underflow. Het getal wordt zo klein dat een rekenmachine of computer het soms gewoon als 0 afrondt.

• Met logaritmen

Om dit beter te kunnen hanteren gebruiken wiskundigen logaritmen:

\[log_{10}((0.000002)^{20}) = 20 . log_{10}(0.000002) = -113.9794001\]

Logaritmen zijn hier krachtig omdat ze een moeilijke bewerking (veelvoudige vermenigvuldiging van kleine getallen) omzetten in een veel eenvoudigere bewerking (optellen van negatieve getallen).

• Het antwoord kan uiteindelijk bekomen door het resultaat terug om te zetten met \(10^x\), indien het datatype float het kan bevatten. In dit geval is het resultaat \(10^{20log_{10}(0.000002)} \approx 10^{-113.9794001} \approx 1.04858e^{-114}\).

• Indien dit niet mogelijk is, behouden we de exponentiële notatie (exponent afgerond op 2 cijfers na de komma).

Opgave

Schrijf een programma dat met behulp van logaritmen het product van extreem kleine getallen kan uitrekenen in wetenschappelijke notatie tot 5 cijfers na de komma. De gebruiker voert hierbij het kleine getal en de exponent in.

Voorbeeld 1

Invoer

0.000002
20

Uitvoer

1.04858e-114

Voorbeeld 2

Invoer

0.00000000009
60

Uitvoer

Er treedt nog steeds underflow op. Het antwoord wordt benaderd door 10^-602.75.