Welk woord plaatsen we in het midden van de rechter driehoek?
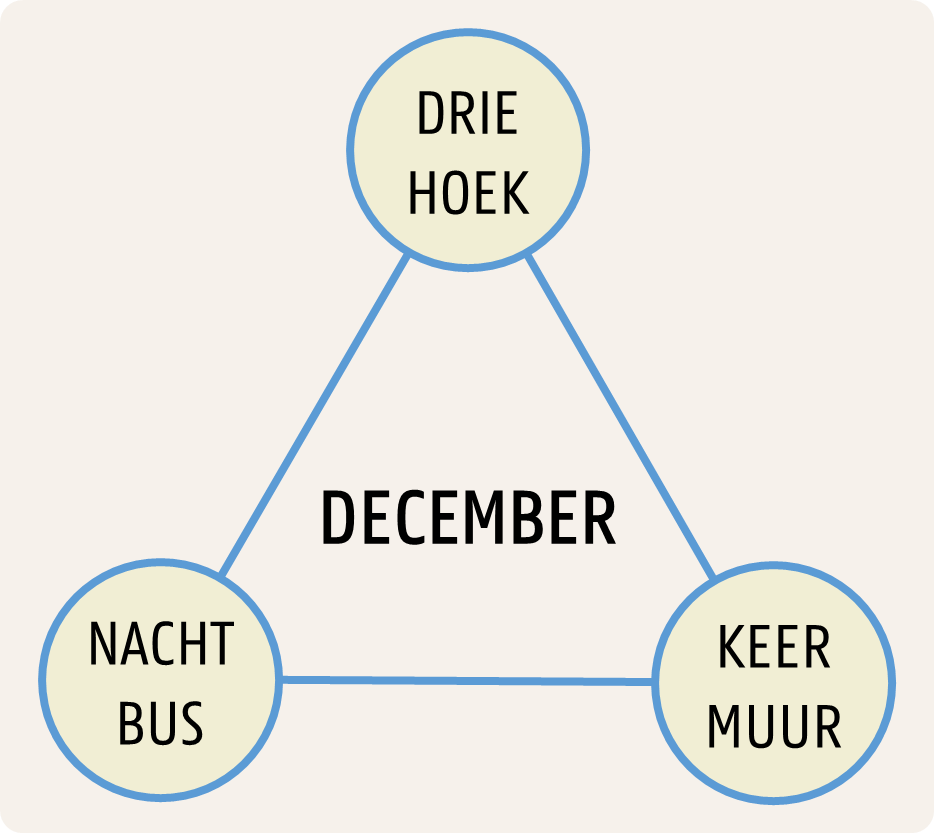
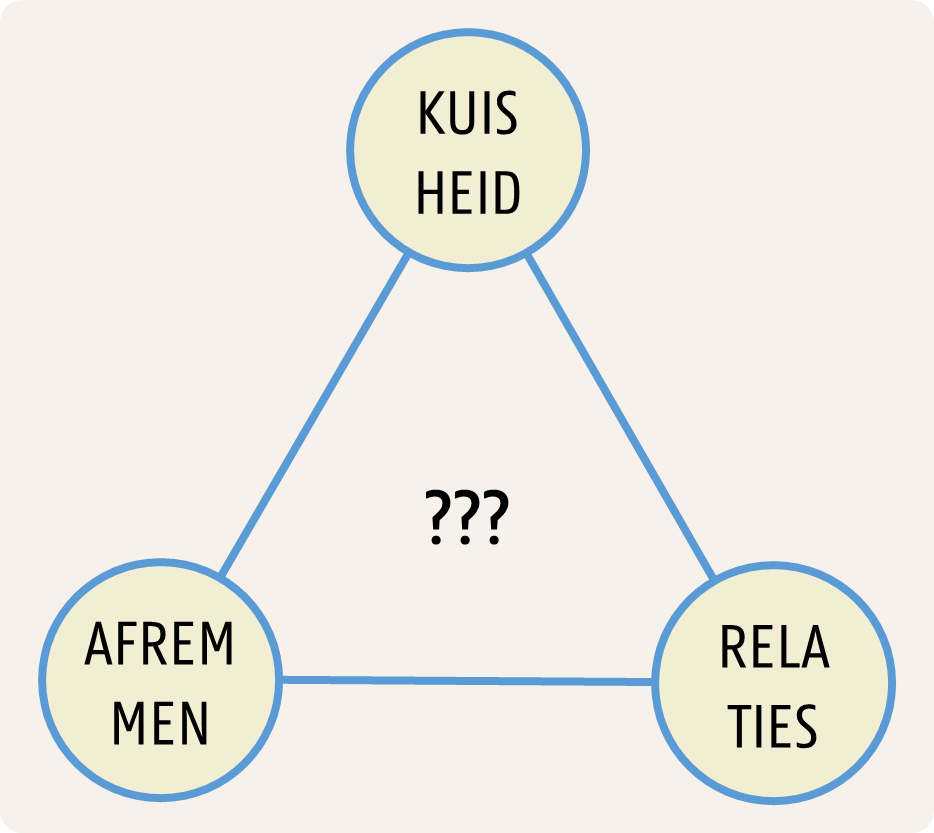
Het gezochte woord is KERSTMIS.
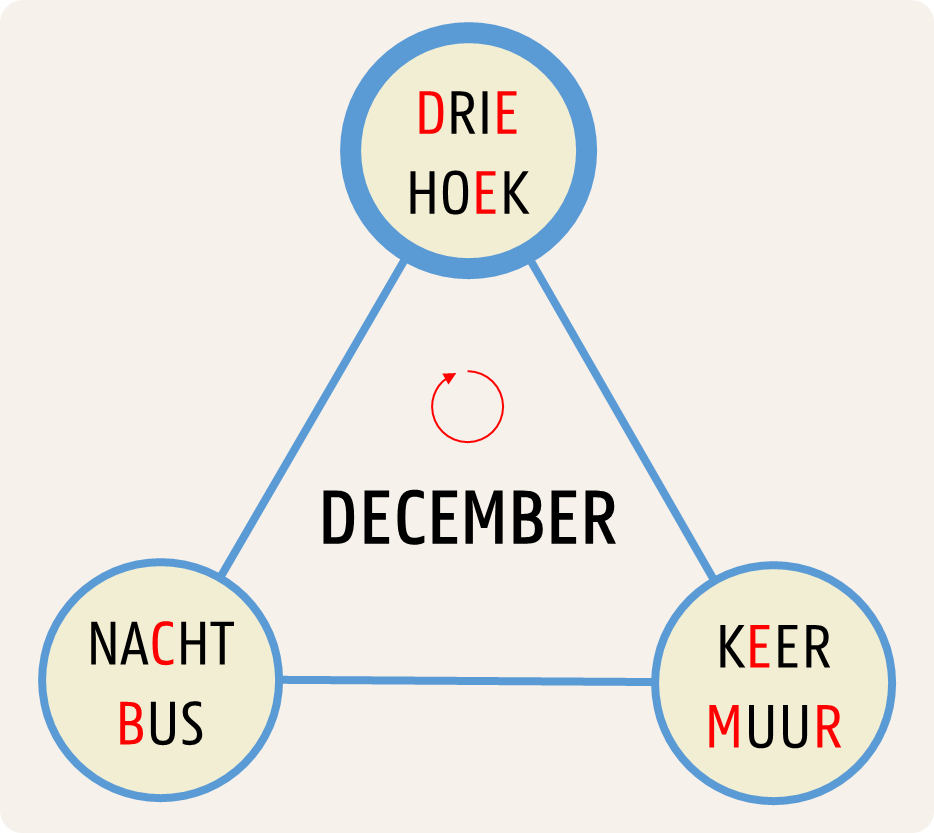
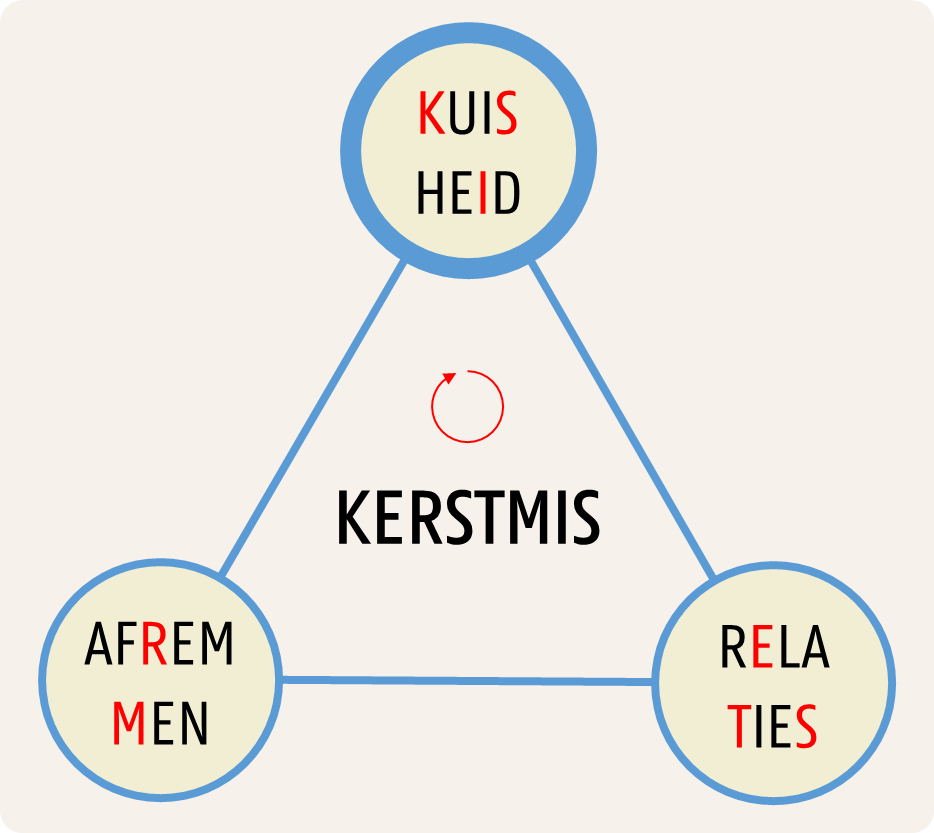
In beide driehoeken zijn alle woorden op de hoekpunten even lang. Het gezochte woord in het midden van de driehoek is even lang als de woorden op de hoekpunten. Het wordt gevonden door te starten bij een hoekpunt (hier telkens het hoekpunt bovenaan met een bredere rand), de hoekpunten in een bepaalde richting af te lopen (hier telkens in wijzerzin) en van de opeenvolgende woorden telkens de letter op de volgende positie te nemen (de eerste letter van het eerste woord, de tweede letter van het tweede woord, enzoverder). We hebben de letters die het gezochte woord vormen in het rood aangeduid.
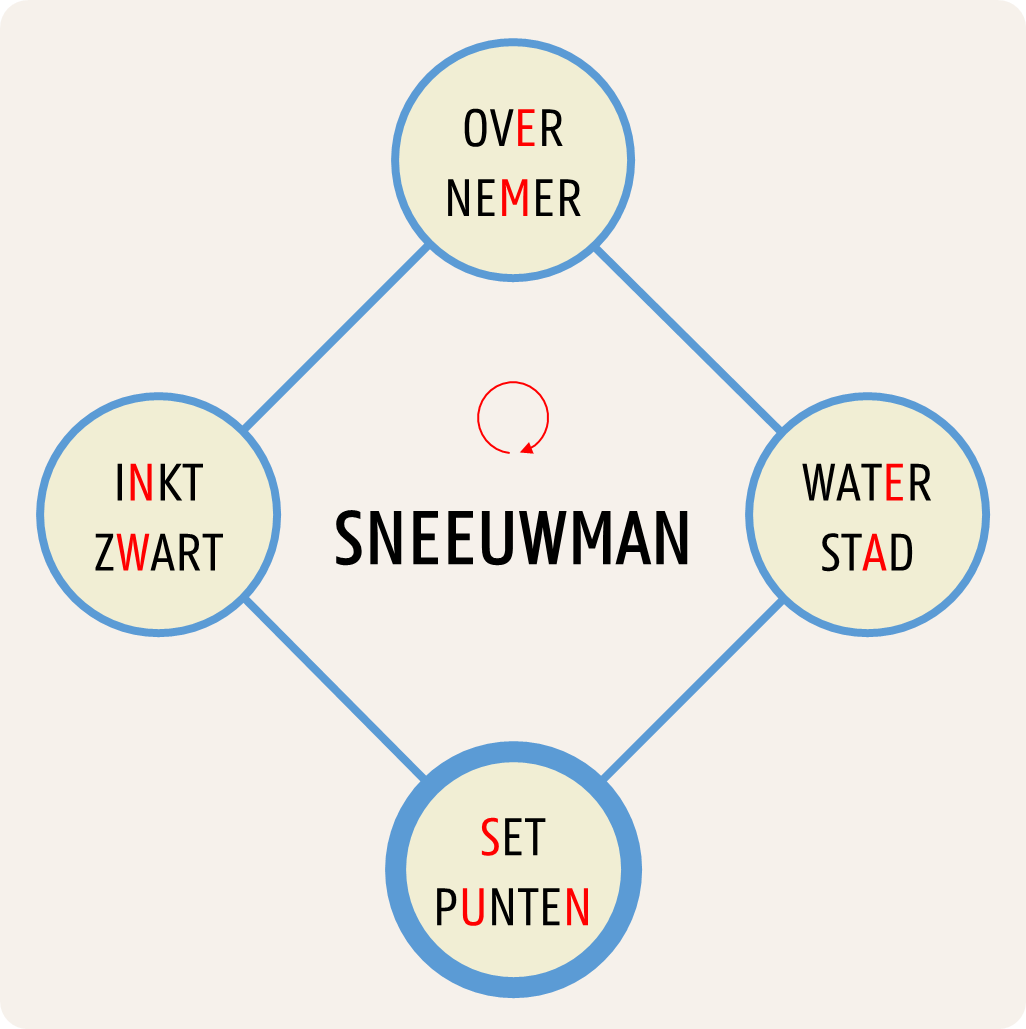
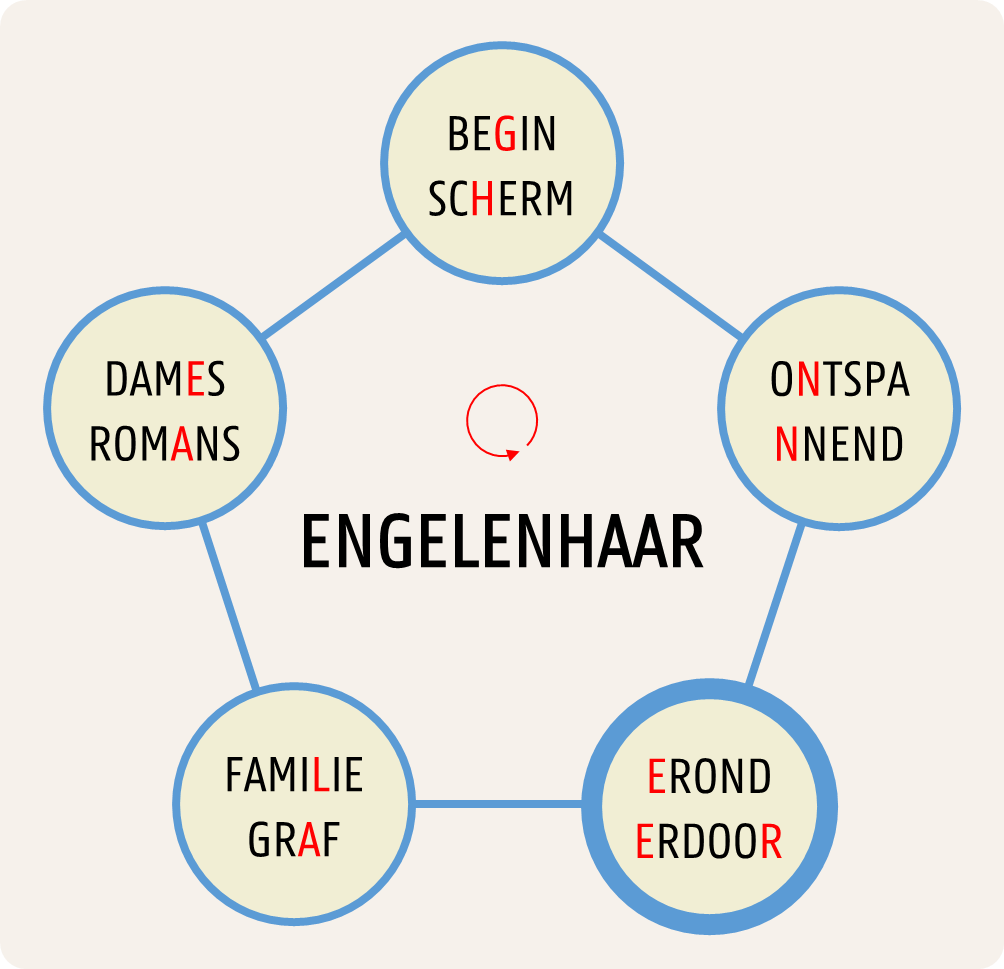
We moeten ons echter niet beperken tot driehoeken: veelhoeken met meer dan drie hoekpunten zijn ook mogelijk. Bovendien moeten we ook niet noodzakelijk bij het bovenste hoekpunt beginnen. Als we bijvoorbeeld in het vierkant hieronder beginnen bij het onderste hoekpunt en de woorden op de hoekpunten in wijzerzin aflopen, dan bekomen we het woord SNEEUWMAN. Het kan ook zijn dat we de hoekpunten in tegenwijzerzin moeten aflopen. Als we bijvoorbeeld in onderstaande vijfhoek beginnen bij het hoekpunt rechtsonder en de woorden op de hoekpunten in tegenwijzerzin aflopen, dan spellen we het woord ENGELENHAAR.
Opgave
Een veelhoek is een puzzel waarbij een reeks woorden met $$m$$ letters op de $$n$$ hoekpunten van een veelhoek geplaatst worden. De puzzel wordt voorgesteld als een reeks (list of tuple)
-
die minstens drie elementen bevat ($$n \geq 3$$)
-
waarvan alle elementen strings (str) zijn die de woorden op de hoekpunten voorstellen (opgelijst in wijzerzin)
-
waarvan alle elementen enkel uit hoofdletters bestaan
-
waarvan alle elementen even lang zijn
Een mogelijke oplossing van een puzzel is een woord (str) van $$m$$ letters dat kan gevonden worden door te starten bij een hoekpunt, de hoekpunten in een bepaalde richting af te lopen (wijzerzin of tegenwijzerzin) en van de opeenvolgende woorden telkens de letter op de volgende positie te nemen. Gevraagd wordt:
-
Schrijf een functie isveelhoek waaraan één argument $$v$$ moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven, die aangeeft of $$v$$ een geldige veelhoek voorstelt.
-
Schrijf een functie oplossing waaraan één argument $$v$$ moet doorgegeven worden. Als $$v$$ geen geldige veelhoek voorstelt, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige veelhoek. Anders moet de functie een mogelijke oplossing van de veelhoek $$v$$ teruggeven, waarbij rekening moet gehouden worden met twee optionele parameters van de functie:
-
start (int; standaardwaarde: 0): index van het startwoord in de veelhoek
-
wijzerzin (bool; standaardwaarde: True): richting waarin de woorden van de veelhoek afgelopen worden: wijzerzin (True) of tegenwijzerzin (False)
-
Schrijf een functie oplossingen waaraan één argument $$v$$ moet doorgegeven worden. Als $$v$$ geen geldige veelhoek voorstelt, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige veelhoek. Anders moet de functie een verzameling (set) teruggeven met alle mogelijke oplossingen van de veelhoek $$v$$. Dit zijn de mogelijke oplossingen waarbij elk woord op een hoekpunt als startwoord kan optreden en waarbij de hoekpunten zowel in wijzerzin als in tegenwijzerzin kunnen doorlopen worden.
De functie heeft ook nog een optionele parameter wijzerzin waaraan een Booleaanse waarde (bool) kan doorgegeven worden. Als de waarde True expliciet wordt doorgegeven aan de parameter wijzerzin dan moeten enkel de mogelijke oplossingen teruggegeven worden die we kunnen bekomen door de hoekpunten in wijzerzin te doorlopen. Als de waarde False expliciet wordt doorgegeven aan de parameter wijzerzin dan moeten enkel de mogelijke oplossingen teruggegeven worden die we kunnen bekomen door de hoekpunten in tegenwijzerzin te doorlopen.
Voorbeeld
>>> isveelhoek(['DRIEHOEK', 'KEERMUUR', 'NACHTBUS'])
True
>>> isveelhoek(('kuisheid', 'RELATIES', 'AFREMMEN'))
False
>>> isveelhoek('SETPUNTEN, INKTZWART, OVERNEMER, WATERSTAD')
False
>>> isveelhoek(('ERONDERDOOR', 'ONTSPANNEND', 'BEGINSCHERM', 3.14, 'FAMILIEGRAF'))
False
>>> oplossing(['DRIEHOEK', 'KEERMUUR', 'NACHTBUS'])
'DECEMBER'
>>> oplossing(('KUISHEID', 'RELATIES', 'AFREMMEN'))
'KERSTMIS'
>>> oplossing(['OVERNEMER', 'WATERSTAD', 'SETPUNTEN', 'INKTZWART'], start=2)
'SNEEUWMAN'
>>> oplossing(('DAMESROMANS', 'BEGINSCHERM', 'ONTSPANNEND', 'ERONDERDOOR', 'FAMILIEGRAF'), start=3, wijzerzin=False)
'ENGELENHAAR'
>>> oplossingen(['DRIEHOEK', 'KEERMUUR', 'NACHTBUS'])
{'DAEETUES', 'DECEMBER', 'KAIRTOUS', 'KRCRHBUK', 'NEIHMOUR', 'NREHHUUK'}
>>> oplossingen(('KUISHEID', 'RELATIES', 'AFREMMEN'), wijzerzin=True)
{'AULEHIED', 'KERSTMIS', 'RFIAMEEN'}
>>> oplossingen(['OVERNEMER', 'WATERSTAD', 'SETPUNTEN', 'INKTZWART'], wijzerzin=True)
{'IVTPZETET', 'OATTNSTRR', 'SNEEUWMAN', 'WEKRRNAED'}
>>> oplossingen(('DAMESROMANS', 'BEGINSCHERM', 'ONTSPANNEND', 'ERONDERDOOR', 'FAMILIEGRAF'), wijzerzin=False)
{'BAMNPSOGONM', 'DAOSNREDERS', 'ENGELENHAAR', 'FRTISIRNENF', 'OEMIDACMROD'}
Bronnen
Epiloog
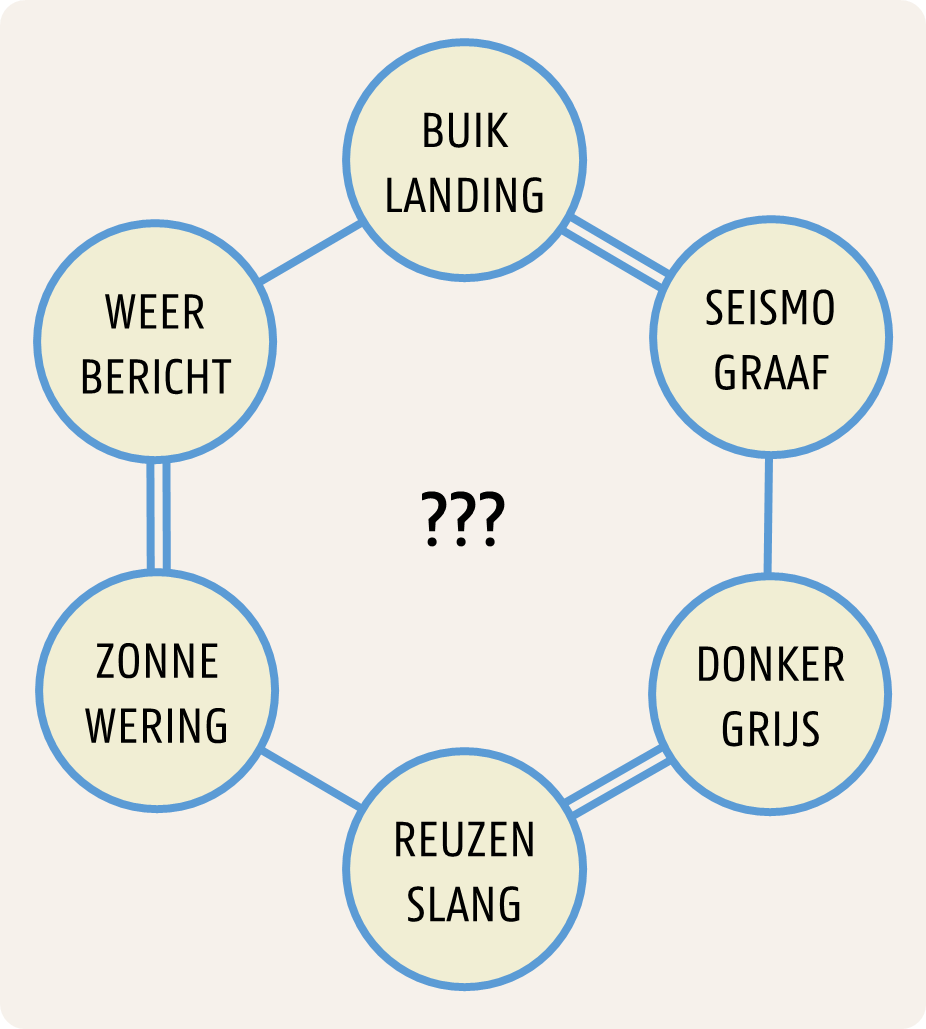
Een zeshoekige puzzel met een extra tip.