ShellSort, genoemd naar zijn uitvinder D.L. Shell, is een sorteeralgoritme dat een rij sorteert door herhaaldelijk een ander sorteeralgoritme toe te passen op verscheidene door elkaar geweven deelrijen van de gegeven rij. Ondanks zijn tijdscomplexiteit met bovengrens \(O(n^2)\), zal ShellSort (mits goed gekozen deelrijen en intern algoritme) zijn ondergrens \(\Omega(n \log n)\) sterk benaderen.
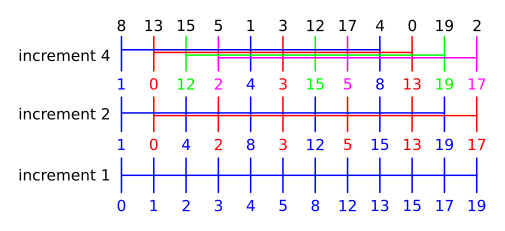
Het bepalen van de deelrijen gebeurt als volgt: in elke fase \(i\) van het algoritme wordt de deelrij gevormd door het doorlopen van de rij met een increment van \(h_i\). De reeks van gebruikte incrementen moet dalend zijn en moet eindigen met \(1\), m.a.w. \(h_1 > \cdots > h_i > \cdots > h_m = 1\). De efficiëntie van het algoritme is sterk afhankelijk van de incrementreeks, met \((1, 4, 13, 40, 121, \dots)\) gekend als één van de beste incrementreeksen.
Zoals vermeld werkt ShellSort met een intern sorteeralgoritme. Hiervoor worden vaak (varianten op) eenvoudige algoritmen als BubbleSort en InsertionSort gebruikt. Belangrijk: om als “goed” intern sorteeralgoritme te kwalificeren, dient het gekozen algoritme (bijna) lineair te presteren op een (bijna) gesorteerde rij.
Implementeer ShellSort in Java. Je krijgt een klasse
Tabel1 en een interface
Sorteerder2. De interface Sorteerder vraagt
de implementatie van één methode, void sorteer(Tabel tabel), die het gegeven
Tabel-object oplopend zal sorteren. Merk op dat er geen nieuwe tabel gegenereerd
wordt, m.a.w. de gegeven tabel zelf dient aangepast te worden door de elementen
ervan te herordenen. Hiervoor voorziet de klasse Tabel de volgende methoden:
int size()geeft terug hoe lang deze tabel is.int get(int index)geeft het getal op positieindexterug.void swap(int i, int j)verwisselt de getallen op positieien positiej.
Schrijf een klasse ShellSorteerder die de interface Sorteerder
implementeert. Deze sorteert de gegeven tabel met ShellSort. Voorzie naast de
sorteer-methode ook een constructor met signatuur public ShellSorteerder(int
incrementreeks[]), waarmee een nieuwe ShellSorteerder aangemaakt kan worden
die gebruik maakt van de gegeven reeks van incrementen (oplopend gesorteerd). Er
wordt automatisch getest op correctheid en efficiëntie voor het hele algoritme
en de tussenresultaten bekomen na het sorteren van de deelrijen per increment.
Gebruik eventueel de testklasse SimpleTest3 om je oplossing lokaal te testen. Je kan hierin eenvoudig extra testgevallen toevoegen.