Helderziende Karl Fulves¹ uit New Jersey (Verenigde Staten) vond het volgende paragnostische trucje uit. Geef een gewone dobbelsteen aan een vriendin en draai je rug naar haar toe. Vraag haar om de dobbelsteen op een tafel te plaatsen. Daarna vraag je haar om de dobbelsteen een kwartslag te draaien: als het bovenste getal even is dan moet ze de dobbelsteen naar het oosten draaien (bovenkant naar rechts), en als het bovenste getal oneven is dan moet ze de dobbelsteen naar het noorden draaien (bovenkant van haar weg). Hierdoor komt een ander getal bovenaan te liggen en kan ze de dobbelsteen opnieuw draaien volgens dezelfde procedure: naar het oosten als de bovenkant even is en naar het noorden als het oneven is.

Nadat ze deze procedure een paar keer heeft toegepast, vraag je haar om verder te doen totdat het getal 1 bovenaan komt te liggen, de dobbelsteen dan nog een laatste keer te draaien en zich dan te concentreren op het getal dat bovenaan ligt. Het lijkt logisch dat er voor het laatste getal vier mogelijkheden zijn, maar toch kan je het correct raden. Hoe kan dat?

Verklaring — na maximaal drie keer draaien herhaalt de dobbelsteen steeds hetzelfde patroon: 1 4 5 6 3 2. Nadat je vriendin de dobbelsteen dus minstens drie keer gedraaid heeft, kan je zonder problemen voorspellen dat na de 1 de 4 bovenaan zal komen te liggen. Omdat de volledige cyclus voorspelbaar is, kan je de truc een paar keer na elkaar herhalen om verschillende eindgetallen te bekomen.

Opgave

Definieer een klasse Dobbelsteen waarmee dobbelstenen kunnen voorgesteld worden in Python die op een bepaalde manier voor je op tafel liggen. Deze dobbelstenen moeten een kwartslag kunnen gedraaid worden in een bepaalde richting, volgens het model dat omschreven wordt in onderstaande figuur. Hierbij worden dobbelstenen op een schematische manier voorgesteld, zodat alle zijden van de dobbelsteen zichtbaar gemaakt worden. Het centrale schema stelt bijvoorbeeld een dobbelsteen voor waarbij de 6 bovenaan ligt, de 3 achteraan, de 4 vooraan, de 2 links, de 5 rechts en de 1 onderaan. De vier andere schema's geven aan hoe de dobbelsteen gaat liggen als je vanuit deze positie de dobbelsteen draait naar het noorden (bovenaan), het zuiden (onderaan), het oosten (rechts) of het westen (links).

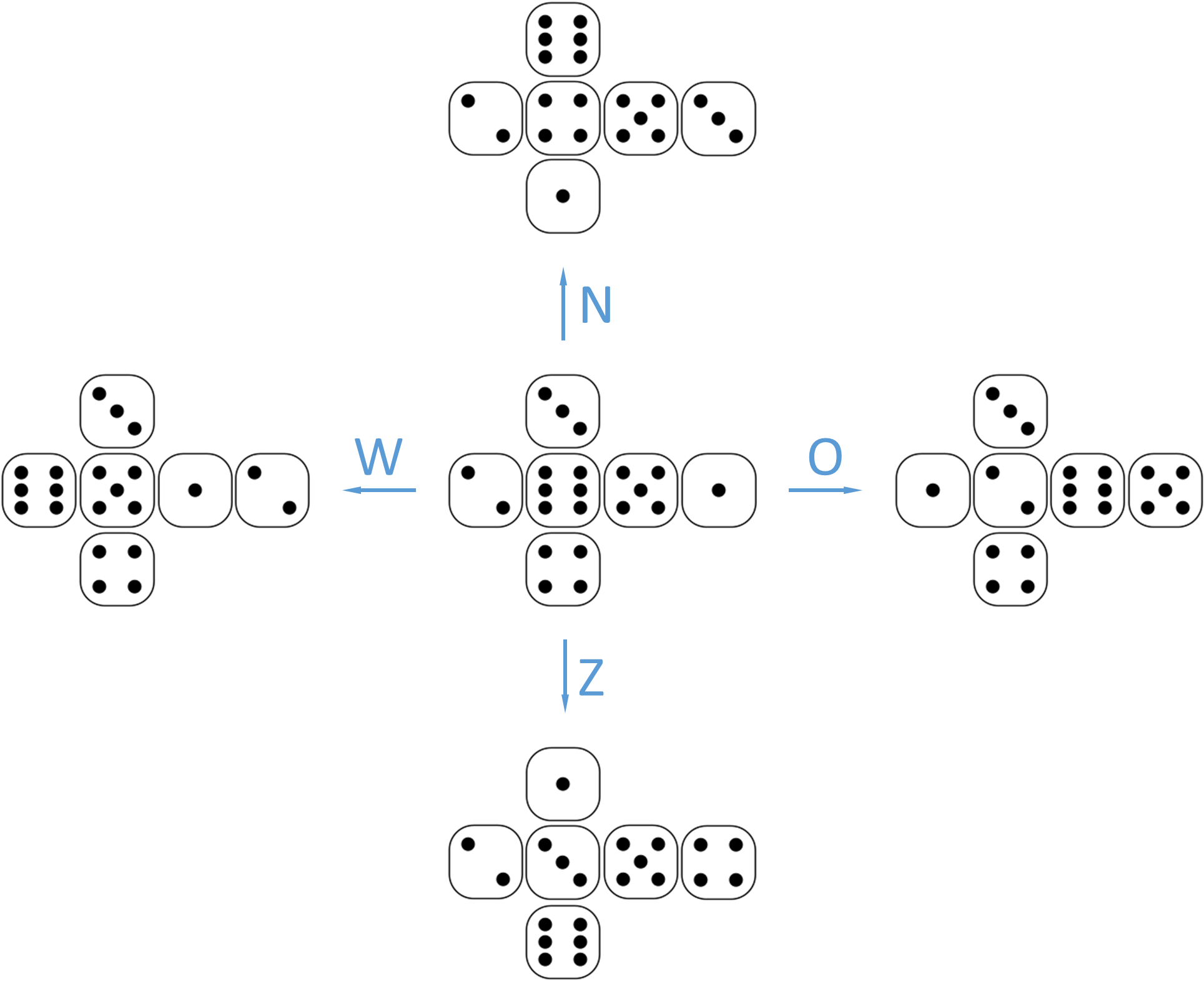
De klasse Dobbelsteen moet minstens de volgende methoden ondersteunen:

• Een initialisatiemethode waaraan geen argumenten kunnen doorgegeven worden. Na initialisatie moet de dobbelsteen gepositioneerd zijn zoals de dobbelsteen die centraal in bovenstaande figuur wordt voorgesteld.

• Een methode bovenkant die teruggeeft hoeveel ogen er op de bovenkant van de dobbelsteen staan.

• Een methode __str__ die een stringvoorstelling van de dobbelsteen teruggeeft die overeenkomt met de schematische voorstelling die gebruikt wordt in bovenstaande figuur. Bestudeer de doctest uit onderstaand voorbeeld om te achterhalen hoe deze stringvoorstelling moet opgemaakt worden. Merk op dat geen enkele regel van deze stringvoorstelling spaties heeft op het einde van regel.

• Een methode draai waaraan een hoofdletter moet doorgegeven worden die aangeeft in welke richting de dobbelsteen moet gedraaid worden: N voor noord, Z voor zuid, O voor oost en W voor west. De methode moet er niet alleen voor zorgen dat de dobbelsteen in de aangegeven richting gedraaid wordt, maar moet ook teruggeven hoeveel ogen er na het draaien op de bovenkant van de dobbelsteen staan. Indien er een ongeldige richting aan de methode wordt doorgegeven, dan mag de dobbelsteen niet gedraaid worden, maar moet de methode een AssertionError opwerpen met de boodschap ongeldige richting.

• Een methode reeks waaraan een eindwaarde (een natuurlijk getal uit het interval $$[1, 6]$$) moet doorgegeven worden. De methode moet een lijst teruggeven van alle getallen die bovenaan komen te liggen als de dobbelsteen gedraaid wordt volgens de procedure die Karl Fulves heeft bedacht. Hierbij moet de procedure minstens drie keer uitgevoerd worden totdat het getal met de gegeven eindwaarde bovenaan de dobbelsteen komt te liggen, en dan moet de procedure nog één keer uitgevoerd worden. Bij het uitvoeren van de procedure moet de dobbelsteen ook telkens in de aangegeven richting gedraaid worden.

Voorbeeld

>>> dobbel = Dobbelsteen()
>>> dobbel.bovenkant()
6
>>> print(dobbel)
  3
2 6 5 1
  4
>>> dobbel.draai('O')
2
>>> print(dobbel)
  3
1 2 6 5
  4
>>> dobbel.draai('W')
6
>>> print(dobbel)
  3
2 6 5 1
  4
>>> dobbel.draai('N')
4
>>> print(dobbel)
  6
2 4 5 3
  1
>>> dobbel.draai('Z')
6
>>> print(dobbel)
  3
2 6 5 1
  4
>>> dobbel.draai('X')
Traceback (most recent call last):
AssertionError: ongeldige richting
>>> dobbel.reeks(1)
[2, 1, 4, 5, 6, 3, 2, 1, 4]
>>> print(dobbel)
  1
5 4 2 3
  6
>>> dobbel.reeks(3)
[5, 6, 3, 2]
>>> print(dobbel)
  3
1 2 6 5
  4