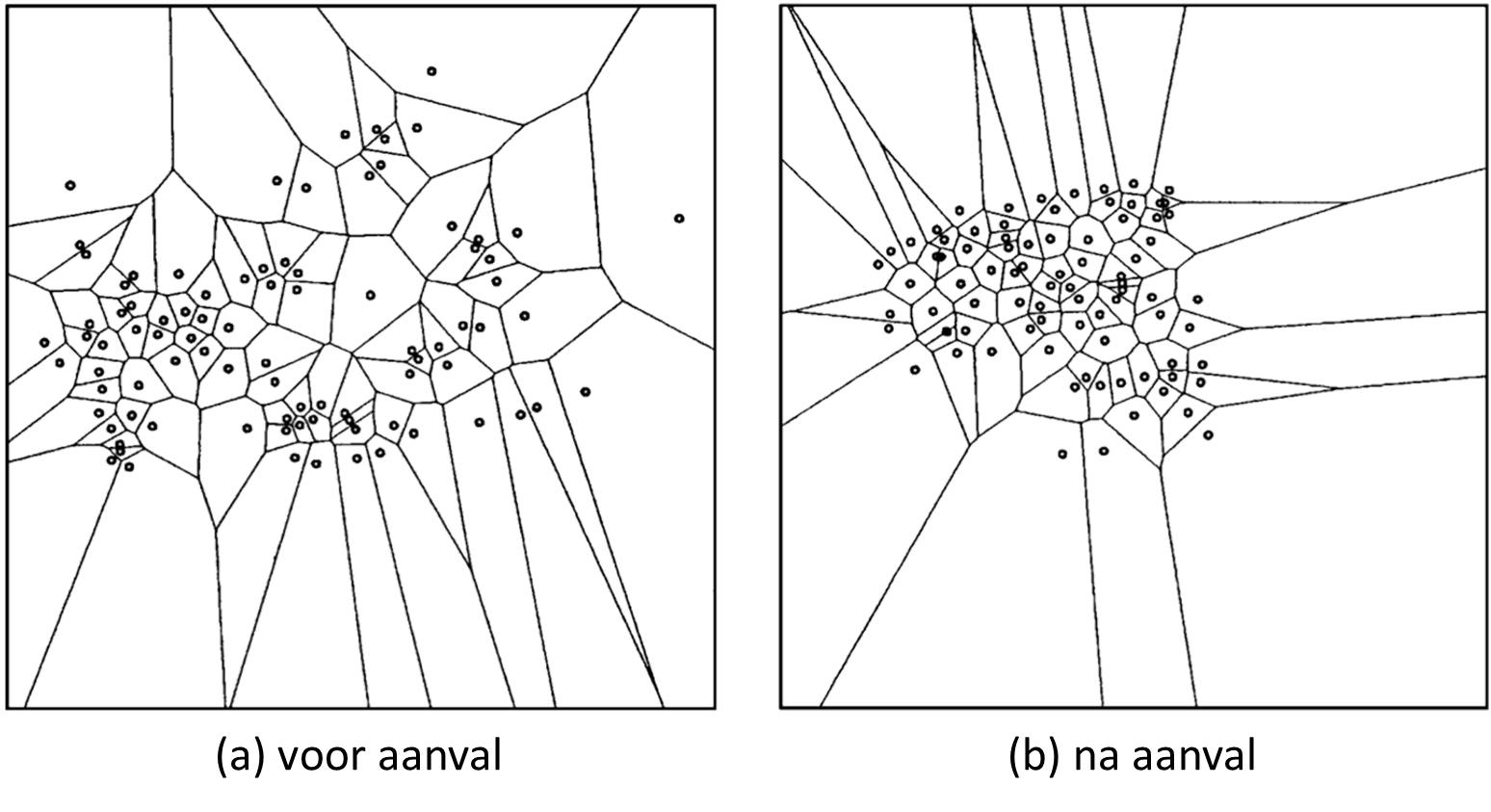
Als een leeuw op een kudde antilopen jaagt, welke regels bepalen dan het gedrag van de kudde? Een intrigerende mogelijkheid staat bekend als de zelfzuchtige kuddetheorie1 (selfish herd theory): in plaats van te handelen in het voordeel van de ganse groep, probeert elk dier zich te positioneren zodat er zich ten minste één ander dier tussen hemzelf en het roofdier bevindt. Dit vormt een patroon dat bekend staat als een Voronoi-betegeling2 — als elk zwart punt in onderstaand diagram een antilope is, dan is de omliggende gekleurde regio het gebied van alle punten die dichter bij die antilope liggen dan bij gelijk welke andere antilope. Als een leeuw jouw regio binnenkomt, dan ben jij de antilope die zal opgegeten worden.

Dit inzicht helpt om bepaalde vormen van kuddegedrag te verklaren. Elk dier wil immers zijn "gevarenregio" zo klein mogelijk maken en zich zo ver mogelijk van het roofdier bevinden. Dominante dieren hebben de neiging om de meest gunstige posities nabij het midden in te nemen, terwijl ondergeschikte dieren naar de randen geduwd worden. De hele formatie evolueert continu terwijl roofdier en prooi zich verplaatsen.

Studies hebben aangetoond dat kolonies wenkkrabben3 de neiging hebben om zich bijzonder snel op te stellen volgens Voronoi-patronen wanneer een roofdier ten tonele verschijnt, en om dichter samen te hokken naarmate het gevaar toeneemt omdat elke krab probeert om zijn omliggende veelhoek kleiner te maken. Dit leidt er in feite toe dat sommige krabben zich dichter naar het roofdier verplaatsen in een poging om het centrum te bereiken en andere krabben tussen zichzelf en de jager te positioneren. Krabben die de bewegingsregels overtreden, hebben de neiging om er uitgepikt te worden, wat de evolutionaire kracht van de strategie verder versterkt.
Opgave
Beschouw een rechthoekig gebied waarin een kudde antilopen aan het grazen is. We delen het gebied op in cellen die een rechthoekig rooster vormen, zodat elke cel hoogstens één antilope bevat. De cellen van het rooster waarin er zich een antilope bevindt markeren we met een unieke hoofdletter. De overige cellen markeren we met een punt. Daardoor kunnen de posities van de antilopen in het gebied aangegeven worden op een kaart die de volgende vorm aanneemt:
......B..
.........
...A.....
.........
.......D.
.........
.C.......
.....E...
.........De positie van een cel in het rooster wordt voorgesteld door een tuple $$(r, k)$$. Hierbij stelt $$r$$ (int) het rijnummer en $$k$$ (int) het kolomnummer voor van de cel in het rooster. De rijen en kolommen van het rooster worden respectievelijk van boven naar onder en van links naar rechts genummerd vanaf 0.
Je opdracht bestaat erin om aan de hand van een Voronoi-betegeling het gebied in te delen in regio's rond de verschillende antilopen. De regio rond een antilope bestaat uit de cel waarin de antilope zich bevindt, samen met alle andere cellen die zich dichter bij die antilope bevinden dan bij elke andere antilope. Hierbij gebruiken we verschillende definities voor het bepalen van de afstand tussen twee cellen op posities $$(x_1, y_1)$$ en $$(x_2, y_2)$$ in het rooster:
| naam | formule |
|---|---|
| Euclidische afstand | $$d=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$$ |
| Manhattan-afstand | $$d=|x_1-x_2| + |y_1-y_2|$$ |
| schaakbord-afstand | $$d=\max(|x_1-x_2|,|y_1-y_2|)$$ |
Onderstaande diagrammen tonen aan dat de formule die gebruikt wordt om de afstand te bepalen wel degelijk een invloed heeft op de vorm van de regio's in de Voronoi-betegeling.


Een afstandsfunctie is een functie waaraan de posities van twee punten in het vlak moeten doorgegeven worden. De positie van een punt in het vlak is een tuple $$(x, y)$$ met $$x, y \in \mathbb{R}$$ (float). Een afstandsfunctie geeft altijd een reëel getal (float) terug dat de afstand uitdrukt tussen de twee gegeven punten volgens een bepaalde afstandsdefinitie. Gevraagd wordt:
-
Schrijf drie afstandsfuncties euclidische_afstand, manhattanafstand en schaakbordafstand die corresponderen met de gelijknamige concepten voor het begrip afstand zoals hierboven gedefinieerd.
-
Schrijf een functie kudde waaraan de locatie (str) moet doorgegeven worden van een tekstbestand met de posities van een kudde antilopen, in het formaat dat hierboven werd beschreven. De functie moet een tuple met drie elementen teruggeven, waarvan de eerste twee respectievelijk het aantal rijen (int) en het aantal kolommen (int) zijn van het rechthoekige rooster waarin het gebied waar de kudde aan het grazen is werd opgedeeld. Het derde element is een dictionary (dict) die de positie van elke cel in het rooster waarin een antilope aan het grazen is afbeeldt op de hoofdletter (str) waarmee de antilope gemarkeerd werd.
-
Schrijf een functie dichtste_antilopen waaraan twee argumenten moeten doorgegeven worden: i) de positie van een cel in het rooster en ii) een dictionary (dict) met de posities van een kudde antilopen. Deze dictionary moet dezelfde vorm hebben als de dictionaries die door de functie kudde worden teruggegeven (als derde element van het tuple). De functie moet een verzameling (set) teruggeven met de labels (str; hoofdletters) van de antilopen in alle cellen die zich het dichtst bij de gegeven cel bevinden.
-
Schrijf een functie regios waaraan de locatie (str) moet doorgegeven worden van een tekstbestand met de posities van een kudde antilopen, in het formaat dat hierboven werd beschreven. De functie moet een string (str) teruggeven met het rooster uit het gegeven tekstbestand, waarbij elke cel die gemarkeerd werd door een punt wordt voorgesteld door een kleine letter die overeenkomt met het label van de dichtstbijzijnde antilope (cf. functie dichtste_antilopen). De alfabetisch eerste letter moet gebruikt worden als er meerdere antilopen zijn die het dichtst bij die cel staan.
Voor het bepalen van de afstand tussen twee cellen van een rooster moeten de functies dichtste_antilopen en regios gebruikmaken van een afstandsfunctie die kan doorgegeven worden aan een optionele parameter afstand. De Euclidische afstand moet gebruikt worden indien er niet expliciet een waarde wordt doorgegeven aan deze parameter.
Voorbeeld
In onderstaande voorbeeldsessie gaan we ervan uit dat het bestand kudde.txt4 zich in de huidige directory bevindt.
>>> euclidische_afstand((0, 0), (3, 4)) 5.0 >>> manhattanafstand((0, 0), (3, 4)) 7.0 >>> schaakbordafstand((0, 0), (3, 4)) 4.0 >>> kudde('kudde.txt5') (9, 9, {(2, 3): 'A', (0, 6): 'B', (6, 1): 'C', (4, 7): 'D', (7, 5): 'E'}) >>> posities = {(2, 3): 'A', (0, 6): 'B', (6, 1): 'C', (4, 7): 'D', (7, 5): 'E'} >>> dichtste_antilopen((0, 0), posities) {'A'} >>> dichtste_antilopen((3, 5), posities, afstand=manhattanafstand) {'A', 'D'} >>> dichtste_antilopen((2, 5), posities, afstand=schaakbordafstand) {'A', 'B', 'D'} >>> print(regios('kudde.txt6')) aaaabbBbb aaaaabbbb aaaAaabdd aaaaaaddd ccaaaddDd cccceeddd cCcceeedd ccceeEeee ccceeeeee >>> print(regios('kudde.txt7', afstand=manhattanafstand)) aaaabbBbb aaaaabbbb aaaAaabdd aaaaaaddd ccaaaddDd cccaeeddd cCcceeedd ccceeEeee ccceeeeee >>> print(regios('kudde.txt8', afstand=schaakbordafstand)) aaaaabBbb aaaaabbbb aaaAaabbb aaaaaaddd caaaaadDd ccccedddd cCcceeedd cccceEeed cccceeeee