De Inca en andere Zuid-Amerikaanse volkeren in de Andesregio maakten gebruik van quipus (ook khipus of sprekende knopen genoemd): een registratiesysteem dat bestaat uit een reeks geknoopte touwen. Het woord khipu stamt uit het Cusco-Calloa Quecha-dialect (Peru) en betekent knoop of het werkwoord knopen. Een quipu bestaat doorgaans uit gekleurde, gesponnen en gevlochten touwen van katoen of camelidevezel. Quipus werden gebruikt voor het verzamelen en archiveren van gegevens zoals openstaande belastingen, bevolkingsaantallen, agenda's en militaire structuren. Er zijn maar een beperkt aantal quipus bewaard. Sommige daarvan bestaan slechts uit een handvol touwen, maar er werden ook zeer complexe quipus gevonden die wel 2000 touwen bevatten.

Quipus hebben zeker nog niet al hun geheimen prijsgegeven, maar ondertussen staat wel al vast dat de geregistreerde informatie meestal bestaat uit getallen in het decimaal talstelsel. Na analyse van honderden quipus slaagden Marcia en Robert Ascher erin om de code te ontcijferen die toelaat om de getallen te lezen.
Een touw kan één of meer getallen registreren. Deze getallen worden voorgesteld als een opeenvolging van knopenclusters die moeten gelezen worden vanaf het hoofdtouw: het touw waaraan de andere touwen bevestigd zijn (bovenaan onderstaande figuur). Een cluster van knopen stelt één enkel cijfer voor, waarbij gebruikgemaakt wordt van drie soorten knopen: eenvoudige overhandse knopen, achtknopen en lange knopen (overhandse knopen met één of meer bijkomende omwentelingen).
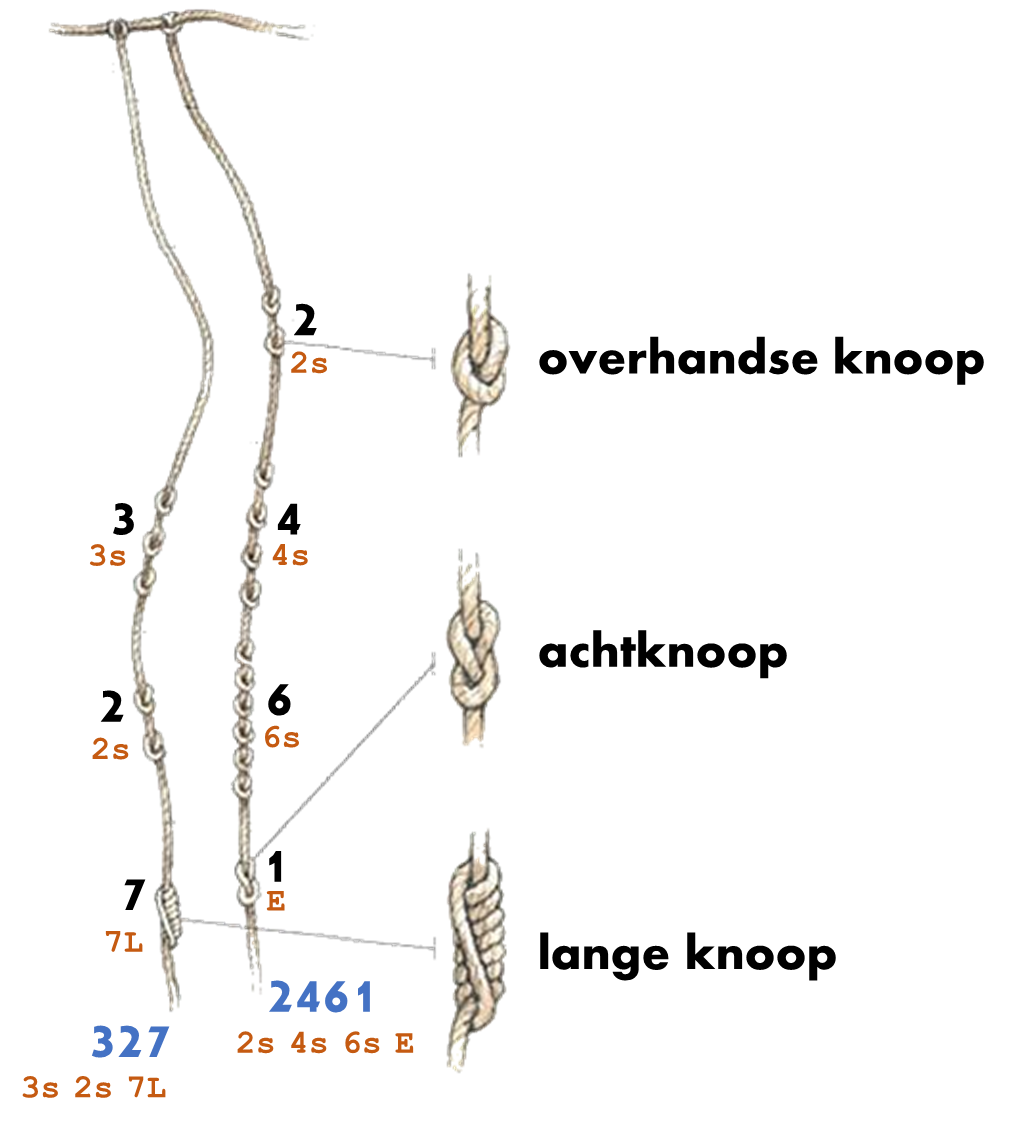
Bij hun analyse van quipus introduceerden de Aschers een eenvoudige notatie voor een cluster van knopen. Ze ontdekten immers dat een natuurlijk getal $$c_{n}c_{n - 1}c_{n - 2}\ldots c_{2}c_{1}c_{0}$$ — waarbij $$c_i (i = 0, 1, \ldots, n)$$ de cijfers $$0, 1, \ldots, 9$$ van een decimaal getal voorstellen — op de volgende manier in knopen vastgelegd wordt. Voor alle cijfers behalve het laatste wordt een nul voorgesteld door een positie zonder knopen (genoteerd als X) en alle andere cijfers door een cluster van $$c_i$$ overhandse knopen (genoteerd als $$c_i$$s). Voor het laatste cijfer wordt een nul voorgesteld door een achtknoop met een extra omwenteling (genoteerd als EE), een één door een gewone achtknoop (genoteerd als E) en alle andere cijfers door een lange knoop met $$c_i$$ omwentelingen (genoteerd als $$c_i$$L). De notaties van de opeenvolgende knopenclusters worden telkens van elkaar gescheiden door een spatie.
Omdat het cijfer van de eenheden (het laatste cijfer van een natuurlijk getal) wordt voorgesteld door karakteristieke knopen, is het meteen ook duidelijk waar een getal eindigt. Daardoor kunnen er op één touw meerdere getallen na elkaar geregistreerd worden. Dit wordt samengevat in onderstaand diagram.
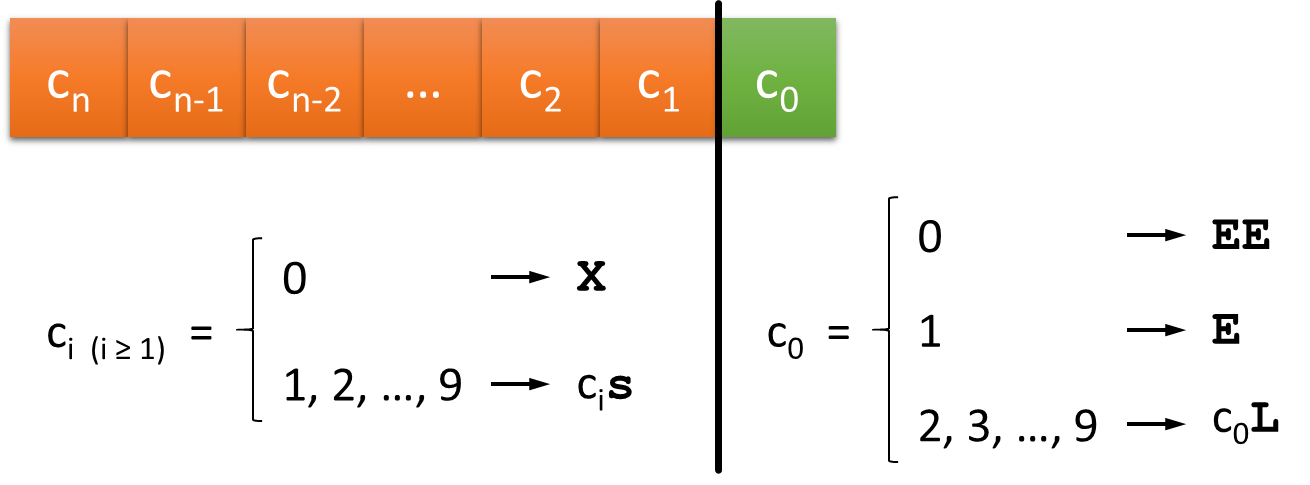
Als bijvoorbeeld 3s staat voor een cluster van drie overhandse knopen, 7L voor een lange knoop met zeven omwentelingen, E voor een achtknoop en X voor een positie zonder knopen, dan
-
wordt het getal 327 genoteerd als 3s 2s 7L
-
wordt het getal 2461 genoteerd als 2s 4s 6s E
-
wordt het getal 107 gevolgd door het getal 51 genoteerd als 1s X 7L 5s E
Deze interpretatie van de knopen wordt bevestigd door een gelukkig toeval: er is immers een systematische manier waarop sommen worden voorgesteld in quipus. Een touw kan bijvoorbeeld de som bevatten van de $$n$$ touwen die erop volgen. Soms worden deze $$n$$ touwen zelfs expliciet aan het touw met de som bevestigd in plaats van aan het hoofdtouw. Er werden ook quipus gevonden waarin de verbindingen van de touwen overeenkomen met sommen van sommen. Dergelijke structuren zouden zeer onwaarschijnlijk zijn als de knopen op een verkeerde manier werden uitgelezen.
Opgave
Definieer de volgende twee functies die kunnen gebruikt worden om de decimale voorstelling van een getal $$n \in \mathbb{N}$$ (int) om te zetten naar de knopenvoorstelling van $$n$$ op een quipu in de Aschernotatie (str), en omgekeerd.
-
Schrijf een functie decimaal2ascher waaraan een decimaal getal $$n \in \mathbb{N}$$ (int) moet doorgegeven worden. Als het argument dat aan de functie wordt doorgegeven geen positieve integer is, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige quipu. Anders moet de knopenvoorstelling van $$n$$ op een quipu in de Aschernotatie (str) teruggeven worden.
-
Schrijf een functie ascher2decimaal waaraan de knopenvoorstelling van een natuurlijk getal op een quipu in de Aschernotatie (str) moet doorgegeven worden. Als het argument dat aan de functie wordt doorgegeven geen string is met een geldige knopenvoorstelling in Aschernotatie van een natuurlijke getal op een quipu, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige quipu. Anders moet de decimale voorstelling van het getal (int) teruggegeven worden.
Definieer nu ook nog een klasse Quipu die toelaat om te rekenen met quipus in Python. Nieuwe objecten van deze klasse moeten zowel geïnitialiseerd kunnen worden met de decimale voorstelling van een getal $$n \in \mathbb{N}$$ (int) als met de knopenvoorstelling van $$n$$ op een quipu in de Aschernotatie (str). Voor andere waarden moet bij initialisatie een AssertionError opgeworpen worden met de boodschap ongeldige quipu.
De conversie van een quipu (een object van de klasse Quipu) naar een string — bekomen met de ingebouwde functies str() en repr() — bevat telkens de knopenvoorstelling op een quipu in Aschernotatie (het verschil in resultaat dat beide ingebouwde functies teruggeven kan je afleiden uit onderstaand voorbeeld) en de conversie naar een integer — bekomen met de ingebouwde functie int() — geeft de decimale waarde terug.
Zorg ervoor dat de binaire operatoren voor de optelling (+), aftrekking (-), vermenigvuldiging (*), gehele deling (//), modulo (%) en machtsverheffing (**) telkens een nieuwe quipu (een object van de klasse Quipu) opleveren als beide operandi quipus zijn of als één van beide operandi een quipu is en het ander een integer. Het resultaat van die bewerkingen moet dezelfde decimale waarde hebben als het resultaat dat deze operatoren opleveren voor twee integer operandi met dezelfde decimale waarde. Als de operator geen geldige quipu oplevert, dan moet een AssertionError opgeworpen worden met de boodschap ongeldige quipu.
Voorbeeld
>>> decimaal2ascher(327)
'3s 2s 7L'
>>> decimaal2ascher(2461)
'2s 4s 6s E'
>>> decimaal2ascher(107)
'1s X 7L'
>>> decimaal2ascher(-1)
Traceback (most recent call last):
AssertionError: ongeldige quipu
>>> ascher2decimaal('3s 2s 7L')
327
>>> ascher2decimaal('2s 4s 6s E')
2461
>>> ascher2decimaal('1s X 7L')
107
>>> ascher2decimaal('5s 17s 4L')
Traceback (most recent call last):
AssertionError: ongeldige quipu
>>> getal = Quipu('3s 2s 7L')
>>> int(getal)
327
>>> str(getal)
'3s 2s 7L'
>>> getal
Quipu('3s 2s 7L')
>>> getal = Quipu(2461)
>>> int(getal)
2461
>>> str(getal)
'2s 4s 6s E'
>>> getal
Quipu('2s 4s 6s E')
>>> Quipu(42) + Quipu(16)
Quipu('5s 8L')
>>> Quipu(42) - Quipu(16)
Quipu('2s 6L')
>>> Quipu(42) * Quipu(16)
Quipu('6s 7s 2L')
>>> Quipu(42) // Quipu(16)
Quipu('2L')
>>> Quipu(42) % Quipu(16)
Quipu('1s EE')
>>> Quipu(12) ** Quipu(2)
Quipu('1s 4s 4L')
>>> Quipu(42) + 16
Quipu('5s 8L')
>>> Quipu(42) - 16
Quipu('2s 6L')
>>> Quipu(42) * 16
Quipu('6s 7s 2L')
>>> Quipu(42) // 16
Quipu('2L')
>>> Quipu(42) % 16
Quipu('1s EE')
>>> Quipu(12) ** 2
Quipu('1s 4s 4L')
>>> 42 + Quipu(16)
Quipu('5s 8L')
>>> 42 - Quipu(16)
Quipu('2s 6L')
>>> 42 * Quipu(16)
Quipu('6s 7s 2L')
>>> 42 // Quipu(16)
Quipu('2L')
>>> 42 % Quipu(16)
Quipu('1s EE')
>>> 12 ** Quipu(2)
Quipu('1s 4s 4L')
>>> Quipu('5s 17s 4L')
Traceback (most recent call last):
AssertionError: ongeldige quipu
>>> Quipu(-1)
Traceback (most recent call last):
AssertionError: ongeldige quipu
>>> Quipu({1, 2, 3})
Traceback (most recent call last):
AssertionError: ongeldige quipu
>>> Quipu(16) - Quipu(42)
Traceback (most recent call last):
AssertionError: ongeldige quipu