Beschouw een vierkant $$n \times n$$ rooster waarvan elke cel gelabeld is. De labels kunnen zowel integers als strings zijn. Cellen die hetzelfde label dragen vormen een groep. De labels vormen een evendeling van het rooster als elke groep bestaat uit $$n$$ cellen en als de groep samenhangend is. Twee cellen worden aangrenzend genoemd als ze een gemeenschappelijke zijde hebben, en op die manier moeten de cellen van een samenhangende groep een aangrenzend geheel vormen.

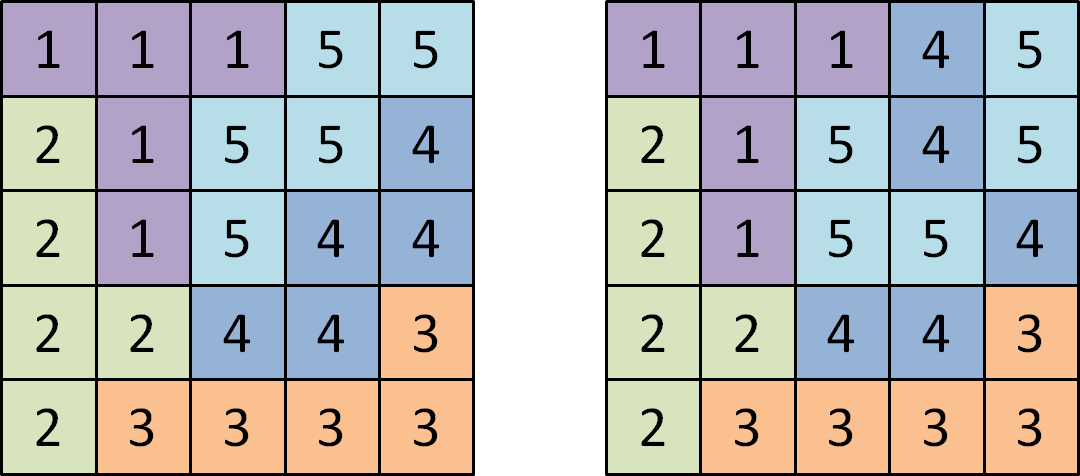
De cellen van deze twee $$5 \times 5$$ roosters zijn gelabeld met de getallen tussen 1 en 5. Daarbij ontstaan telkens groepen van 5 cellen, maar enkel in het linker rooster zijn die allemaal samenhangend. Het linker rooster is dus een evendeling, het rechter rooster is dat niet (groepen 4 en 5 zijn niet samenhangend).

Opgave

We stellen een vierkant gelabeld rooster voor als een reeks (list of tuple) met de rijen van het rooster, opgelijst van boven naar onder. Een rij wordt zelf voorgesteld als een reeks (list of tuple) met de labels op die rij, opgelijst van links naar rechts.

De positie van een cel in een rooster wordt beschreven door een tuple $$(r, k)$$, waarbij $$r$$ het rijnummer (int) van de cel in het rooster aangeeft, en $$k$$ het kolomnummer (int). Rijen worden van boven naar onder genummerd vanaf nul, en kolommen worden van links naar rechts genummerd vanaf nul.

Gevraagd wordt:

Schrijf een functie groepen waaraan een vierkant gelabeld rooster moet doorgegeven worden. De functie moet een dictionary (dict) teruggeven die elk label van het rooster afbeeldt op een verzameling (set) met de posities van de cellen in het rooster die dat label dragen.
Schrijf een functie issamenhangend waaraan een collectie (list, tuple, set, …) moet doorgegeven worden met de posities van de cellen in een groep. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of de cellen van de groep samenhangend zijn.
Schrijf een functie isevendeling waaraan een vierkant gelabeld rooster moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of het rooster een evendeling vormt.

Tip

De methode issamenhangend kan best geïmplementeerd worden met een flood fill algoritme.

We starten hiervoor met een element $$e$$ uit de collectie met punten $$S$$. We plaatsen $$e$$ in een lijst $$L$$. $$L$$ zal de lijst zijn die alle elementen bevat die we als bereikbaar gelabeld hebben, maar waarvan de buren nog niet noodzakelijk gelabeld zijn. Verwijder $$e$$ uit $$S$$. Vervolgens blijven we de volgende procedure uitvoeren tot $$L$$ leeg is.

neem een element $$f$$ uit $$L$$
verwijder $$f$$ uit $$L$$
voor alle buren $$b$$ van $$f$$ in $$S$$
- voeg $$b$$ toe aan $$L$$
- verwijder $$b$$ uit $$S$$

Als $$L$$ leeg is, zijn alle elementen uit $$S$$ die bereikbaar zijn vanuit $$e$$ verwijderd. Als er dus nog elementen in $$S$$ zijn, is de collectie niet samenhangend.

Voorbeeld

>>> rooster = [[1, 1, 1], [2, 2, 3], [2, 3, 3]]
>>> groepen(rooster)
{1: {(0, 1), (0, 0), (0, 2)}, 2: {(2, 0), (1, 0), (1, 1)}, 3: {(1, 2), (2, 1), (2, 2)}}

>>> rooster = [[1, 1, 1, 5, 5], [2, 1, 5, 5, 4], [2, 1, 5, 4, 4], [2, 2, 4, 4, 3], [2, 3, 3, 3, 3]]
>>> groepen(rooster)
{1: {(0, 1), (0, 0), (0, 2), (2, 1), (1, 1)}, 2: {(3, 0), (2, 0), (1, 0), (3, 1), (4, 0)}, 3: {(4, 1), (4, 4), (3, 4), (4, 3), (4, 2)}, 4: {(3, 2), (2, 3), (2, 4), (1, 4), (3, 3)}, 5: {(1, 2), (0, 3), (1, 3), (2, 2), (0, 4)}}

>>> issamenhangend({(1, 2), (1, 3), (2, 2), (0, 3), (0, 4)})
True
>>> issamenhangend({(1, 2), (1, 4), (2, 2), (0, 3), (0, 4)})
False

>>> rooster = [[1, 1, 1], [2, 2, 3], [2, 3, 3]]
>>> isevendeling(rooster)
True

>>> rooster = [[1, 1, 1], [2, 2, 3], [3, 3, 2]]
>>> isevendeling(rooster)
False

>>> rooster = [[1, 1, 1, 5, 5], [2, 1, 5, 5, 4], [2, 1, 5, 4, 4], [2, 2, 4, 4, 3], [2, 3, 3, 3, 3]]
>>> isevendeling(rooster)
True