In de getaltheorie telt een priemgetal-telfunctie, vaak genoteerd als \(\mathsf{\pi(x)}\), het aantal priemgetallen kleiner dan of gelijk aan een gegeven strikt positief reëel getal x.
De grafiek van de priemgetal-telfunctie ziet er als volgt uit:
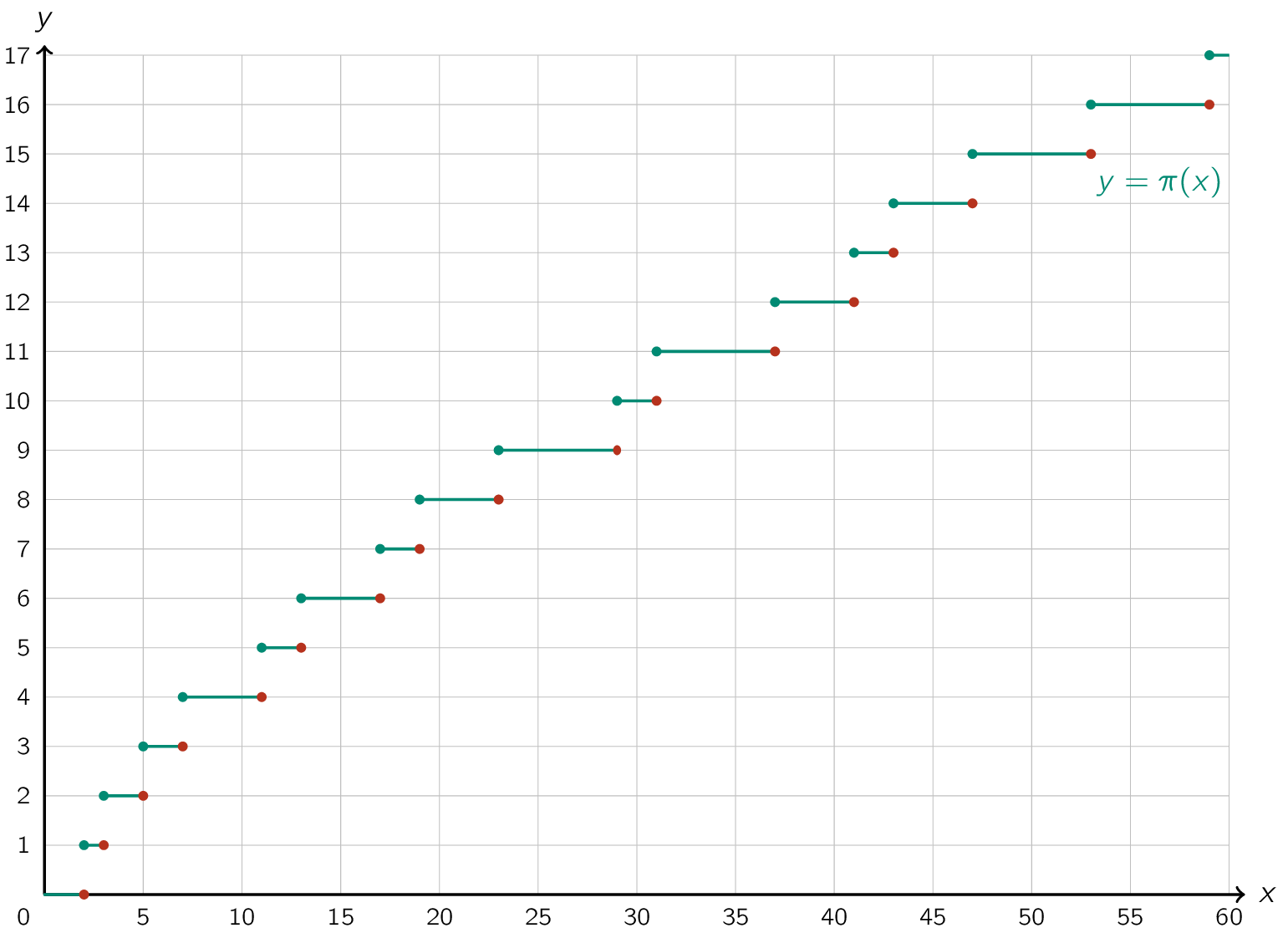
Opgave
Schrijf een functie is_priem(getal) die controleert of een gegeven getal priem is.
Schrijf daarna een functie telpriem(x) dat voor een gegeven (komma)getal x het aantal priemgetallen kleiner dan of gelijk aan dit getal telt.
Schrijf daarna een programma dat aan de gebruiker een (strikt positief) reëel getal vraagt en de priemgetal-telfunctie hierop toepast. Het resultaat van deze functie wordt vervolgens op het scherm weergegeven.
Voorbeelden
Bij invoer 10.0 verschijnt er:
Er zijn 4 priemgetallen kleiner dan of gelijk aan 10.0
>>> telpriem(10.0)
4
Bij invoer 11 verschijnt er:
Er zijn 5 priemgetallen kleiner dan of gelijk aan 11.0
>>> telpriem(11)
5
Bij invoer 100.5 verschijnt er:
Er zijn 25 priemgetalen kleiner dan of gelijk aan 100.5
>>> telpriem(100.5)
25
Tip
Rond het kommagetal af naar beneden… Vergeet hierbij niet om
mathte importeren.