Convolutieproducten vormen een belangrijke bewerking in binnen de signaal- en beeldverwerking. In het onderstaande voorbeeld wordt het eendimensionale geval uiteengedaan. Hetzelfde proces is mogelijk voor twee of meer dimensies (zoals bij beeldverwerking). Ook binnen neurale netwerken vormen convoluties een essentiele bouwsteen.

Omdat de wiskundige definitie vrij ingewikkeld is, wordt er meteen met een voorbeeld gewerkt.

Voor een eendimensionale (discrete) convolutie heb je twee lijsten nodig. Een bronlijst en een lijst genaamd de kernel. Stel bijvoorbeeld dat de bronlijst de lijst [0, 0, 1, 0, 1, 0, 0, 0, 0] en de kernel [0.2, 0.6, 0.4] is.

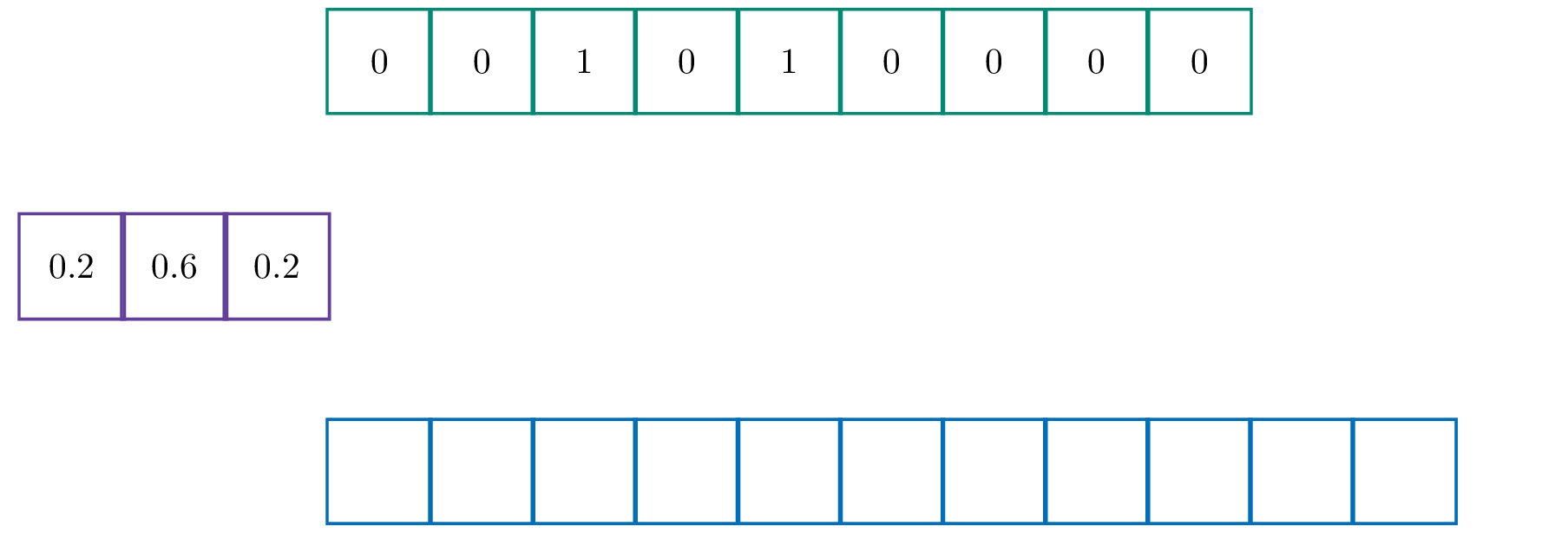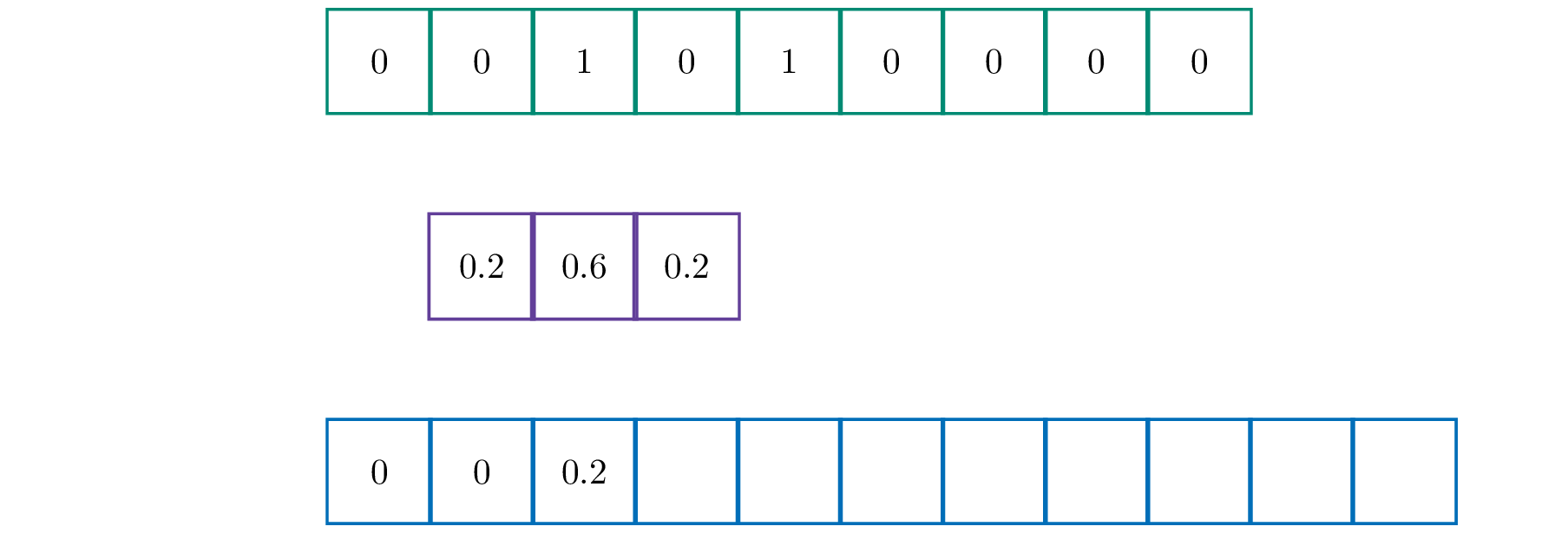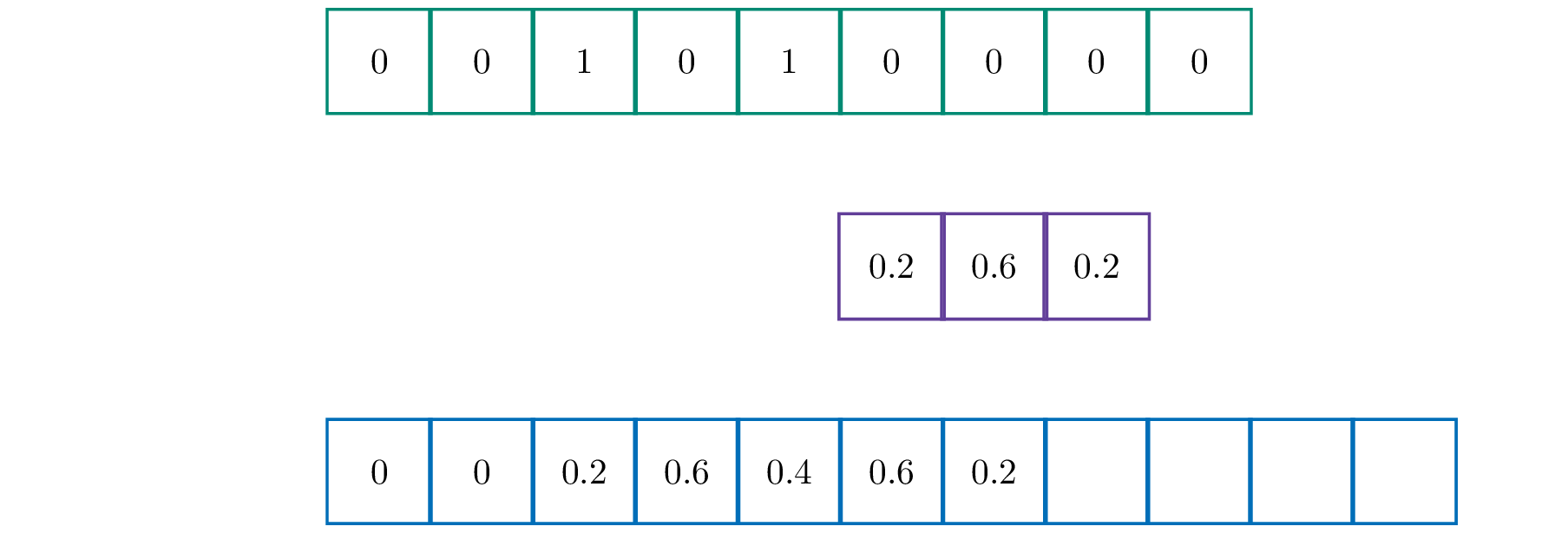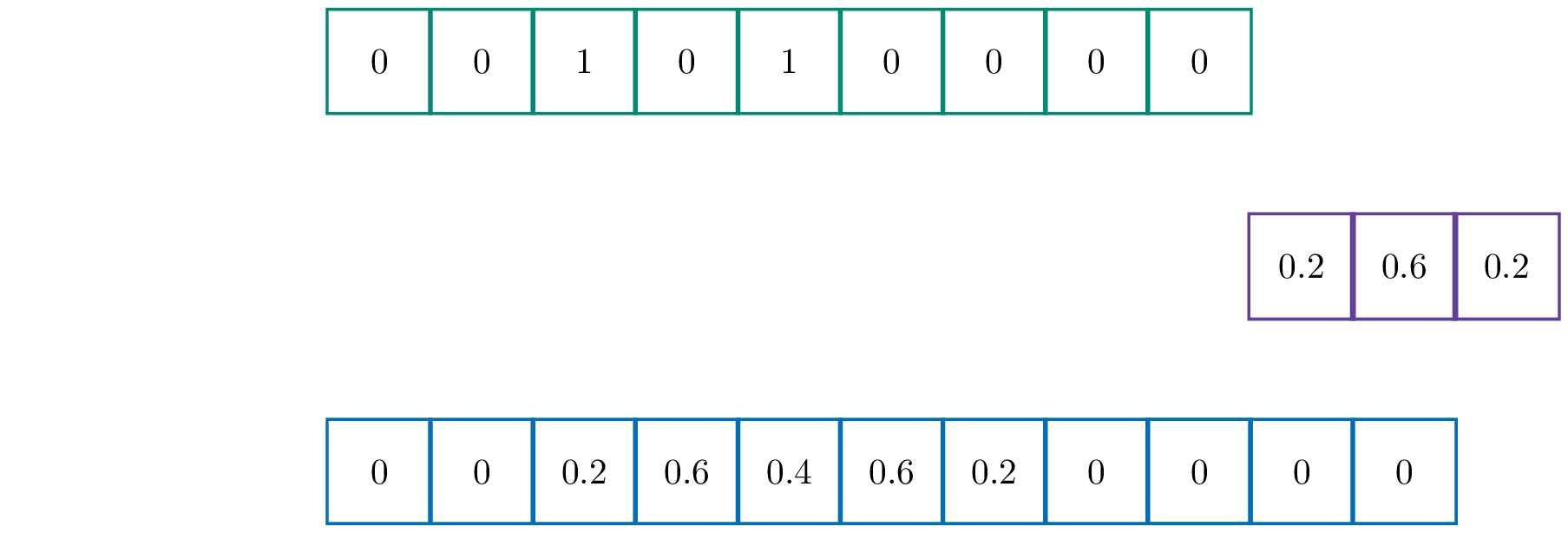
Zoals je merkt schuift de kernel in elke stap op. De waarden uit de bronlijst worden vervolgens vermenigvuldigd met de overeenkomstige waarden in de kernel en het resultaat wordt opgeteld. Het resultaat is een nieuwe lijst die als het ware een vloeiende versie is van de oorspronkelijke lijst.

Opgave

Schrijf een functie convolutie() die gegeven twee lijsten het convolutieproduct uitrekent. Zorg ervoor dat de getallen in de resulterende lijst afgerond worden op twee cijfers na de komma.

Voorbeeld

>>> convolutie( [0, 0, 1, 0, 1, 0, 0, 0, 0] , [0.2, 0.6, 0.2] )
[0.0, 0.0, 0.2, 0.6, 0.4, 0.6, 0.2, 0.0, 0.0, 0.0, 0.0]