Eenzijdig of tweezijdig toetsen?

De test in het captopril voorbeeld was een eenzijdige test. We wensen immers enkel te detecteren of de captopril behandeling de bloeddruk gemiddeld gezien doet dalen.

In andere gevallen of een andere context wenst men enkel een stijging te detecteren.
Stel dat men het bloeddrukverschil had gedefineerd als \(X_{i}^\prime=Y_{i}^\text{voor}-Y_{i}^\text{na}\) dan zouden positieve waarden aangeven dat er een bloeddrukdaling was na de behandeling van captopril: de bloeddruk bij aanvang is dan immers groter dan na de behandeling. De gemiddelde bloeddrukverandering in de populatie noteren we nu als \(\mu^\prime=\text{E}[X^*]\). In dat geval hadden we een eenzijdige test uit moeten voeren om \(H_0: \mu^\prime=0\) te testen tegen \(H_1: \mu^\prime>0\). Voor deze test kunnen we de p-waarde als volgt berekenen:

\[p=\text{P}_0\left[T\geq t\right].\]

We voeren nu de analyse uit in R op basis van de toevallige veranderlijke \(X^\prime\). We zullen nu het argument alternative="greater" gebruiken in de t.test functie zodat we de nulhypothese toetsen tegen het alternatief \(H_1: \mu^\prime>0\):

delta2 <- captopril$SBPb-captopril$SBPa
t.test(delta2,alternative="greater")

## 
##  One Sample t-test
## 
## data:  delta2
## t = 8.1228, df = 14, p-value = 5.732e-07
## alternative hypothesis: true mean is greater than 0
## 95 percent confidence interval:
##  14.82793      Inf
## sample estimates:
## mean of x 
##  18.93333

Uiteraard bekomen we met deze analyse exact dezelfde p-waarde en hetzelfde betrouwbaarheidsinterval. Enkel het teken is omgewisseld.

Naast eenzijdige testen kunnen eveneens tweezijdige testen worden uitgevoerd. Het had gekund dat de onderzoekers de werking van het nieuwe medicijn captopril wensten te testen, maar het werkingsmechanisme nog niet kenden in de ontwerpfase. In dat geval zou het eveneens interessant geweest zijn om zowel een stijging als een daling van de bloeddruk te kunnen detecteren. Hiervoor zou men een tweezijdige toetsstrategie moeten gebruiken waarbij men de nulhypothese

\[H_0: \mu=0\]

gaat testen versus het alternatieve hypothese

\[H_1: \mu\neq0,\]

zodat het gemiddelde onder de alternatieve hypothese verschillend is van \(0\). Het kan zowel een positieve of negatieve afwijking zijn en men weet niet bij aanvang van de studie in welke richting het werkelijk gemiddelde zal afwijken onder de alternatieve hypothese.

We kunnen tweezijdig testen op het \(\alpha=5\%\) significantieniveau door

  1. een kritieke waarde af te leiden:
    • Bij een tweezijdige test kan het effect onder de alternatieve hypothese zowel positief of negatief zijn. Hierdoor zullen we onder de nulhypothese de kans berekenen om onder de nulhypothese een effect te observeren dat meer extreem is dan het resultaat dat werd geobserveerd in de steekproef. In deze context betekent “meer extreem” dat de statistiek groter is in absolute waarde dan het geobserveerde resultaat, want zowel grote (sterk positieve) als kleine (sterk negatieve) waarden zijn een indicatie van een afwijking van de nulhypothese.
      • Om een kritieke waarde af te leiden,zullen we het significatie-niveau \(\alpha\) daarom verdelen over de linker en rechter staart van de verdeling onder \(H_0\). Gezien de t-verdeling symmetrisch is, volgt dat we een kritieke waarde \(c\) kiezen zodat er een kans is van \(\alpha/2=2.5\%\) dat \(T\geq c\) en er \(\alpha/2=2.5\%\) kans is dat \(T\leq -c\). We kunnen dit ook nog als volgt formuleren: Er is onder \(H_0\) \(\alpha=5\%\) kans dat \(\vert T\vert\geq c\) (zie Figuur 22).
  2. We kunnen ook gebruik maken van een tweezijdige p-waarde:
\[\begin{eqnarray*} p&=&\text{P}_0\left[T\leq -|t|\right] + \text{P}_0\left[T\geq |t|\right]\\ &=&\text{P}_0\left[\vert T\vert \geq \vert t \vert\right]\\ &=&\text{P}_0\left[T \geq \vert t \vert\right]\times 2. \end{eqnarray*}\]

We berekenen dus de kans dat de t-statistiek onder \(H_0\) meer extreem is dan de geobserveerde teststatistiek \(t\) in de steekproef. Waarbij meer extreem tweezijdig moet geïnterpreteerd worden. De teststatistiek onder \(H_0\) is meer extreem als hij groter is in absolute waarde dan \(\vert t \vert\), de geobserveerde test statistiek. Gezien de verdeling symmetrisch is, kunnen we ook eerst de kans in de rechter staart van de verdeling berekenen en deze kans vervolgens vermenigvuldigen met 2 zodoende een tweezijdige p-waarde te bekomen.

Als de onderzoekers niet vooraf gedefineerd hadden dat ze enkel een bloeddrukdaling wensten te detecteren, dan hadden ze dus een twee-zijdige test uitgevoerd. Merk op dat het argument alternative van de t.test functie een default waarde heeft alternative="two.sided" zodat er standaard tweezijdig wordt getoetst.

t.test(delta)

## 
##  One Sample t-test
## 
## data:  delta
## t = -8.1228, df = 14, p-value = 1.146e-06
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -23.93258 -13.93409
## sample estimates:
## mean of x 
## -18.93333

We bekomen nog steeds een exteem significant resultaat. De p-waarde is echter dubbel zo groot omdat we tweezijdig testen. We verkrijgen eveneens een tweezijdig betrouwbaarheidsinterval. De tweezijdige toetsstrategie wordt weergegeven in Figuur 22.

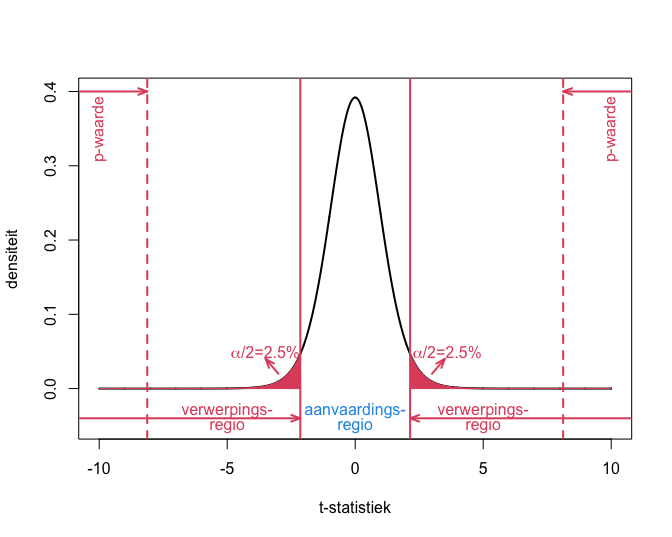
Figuur 22: Interpretatie van p-waarde, kritieke waarde, verwerpingsgebied, aanvaardingsgebied voor het captopril voorbeeld wanneer we een tweezijdige toets uitvoeren.

We kunnen ons nu de vraag stellen wanneer we eenzijdig of tweezijdig toetsen. Met een eenzijdige toets kan men gemakkelijker een alternatieve hypothese aantonen (op voorwaarde dat ze waar is) dan met een tweezijdige toets. Dit komt essentieel omdat bij zo’n toets alle informatie kan worden aangewend om in 1 enkele richting te zoeken. Precies daarom vergt de eenzijdige toets een extra beschouwing vóór de aanvang van de studie. Ook al hebben we sterke a priori vermoedens, vaak kunnen we niet zeker zijn dat dat zo is. Anders was er immers geen reden om dit te willen toetsen.

Als men een eenzijdige test voorstelt, maar men vindt een resultaat in de andere richting dat formeel statistisch significant is, dan is het niet geschikt om dit te zien als bewijs voor een werkelijk effect in die richting. Dat is omdat de onderzoekers die mogelijkheid uitgesloten hebben bij de planning van de studie en het resultaat daarom zó onverwacht is dat het als een vals positief resultaat kan gezien worden. Een eenzijdige test is om die reden niet aanbevolen. Een tweezijdige toets is altijd verdedigbaar omdat ze in principe toelaat om elke afwijking van de nulhypothese te detecteren. Ze worden daarom het meest gebruikt en ten zeerste aangeraden. Het is nooit toegelaten om een tweezijdige toets in een eenzijdige toets om te zetten op basis van wat men observeert in de gegevens! Anders wordt de type I fout van de toetsingsstrategie niet correct gecontroleerd.

Dat wordt geïllustreerd in de onderstaande simulatie. We evalueren twee strategieën, de correcte tweezijdige test en een test waar we eenzijdig toetsen op basis van het teken van het geobserveerde effect.

set.seed(115)
mu <- 0
sigma <- 9.0
nSim <- 1000
alpha <- 0.05
n <- 15
pvalsCor <-
    pvalsInCor <-
    array(0,nSim)

for (i in 1:nSim)
{
    x <- rnorm(n, mean = mu, sd = sigma)
    pvalsCor[i] <- t.test(x)$p.value

    if (mean(x)<0)
        pvalsInCor[i] <- t.test(
            x,
            alternative="less")$p.value else
        pvalsInCor[i] <- t.test(
            x,
            alternative="greater")$p.value
}
mean(pvalsCor < 0.05)

## [1] 0.049

mean(pvalsInCor < 0.05)

## [1] 0.106

We zien inderdaad dat de type I fout correct gecontroleerd wordt op het nominaal significantie-niveau \(\alpha\) wanneer we tweezijdig testen en dat dit helemaal niet het geval is wanneer we eenzijdige toetsen op basis van het teken van het geobserveerde effect.