De Pearson Chi-kwadraat test voor ongepaarde gegevens

We zullen een toets ontwikkelen voor het testen van associatie tussen de categorische blootstelling (bvb. variant, X) en de categorische uitkomst (bvb. ziekte, Y). Concreet zullen we

H_{0} : Er is geen associatie tussen X en Y vs H_{1} : X en Y zijn geassocieerd

testen.

Beschouw de rijtotalen $n_{andere} = a + c$ , $n_{leu,leu} = b + d$ enerzijds en de kolomtotalen $n_{contr} = a + b$ en $n_{case} = c + d$ anderzijds. Zij verstrekken informatie over de marginale verdeling van de blootstelling (bvb. variant, X) en de uitkomst (bvb. ziekte, Y), maar niet over de associatie tussen die veranderlijken. Als de nulhypothese waar is dat $X$ en $Y$ onafhankelijk zijn, dan verwacht men dat een proportie $(b + d) / n$ van $a + b$ controles met een Leu/Leu variant, of dat $(a + b) (b + d) / n$ een Leu/Leu variant hebben omdat een proportie $(b + d) / n$ van alle geobserveerde individuen een Leu/Leu variant heeft. Analoog kan men op basis van de marginale gegevens het verwachte aantal berekenen dat onder de nulhypothese in elke cel van de $2 \times 2$ tabel zou liggen. Dit verwachte aantal onder $H_{0}$ in de $(i, j)$ -de cel (conditioneel op de marges van de tabel) wordt aangeduid met $E_{i j}$ en is het product van het $i$ -de rijtotaal met het $j$ -de kolomtotaal gedeeld door het algemene totaal. In bovenstaand voorbeeld vinden we

$E_{11}$ = het verwachte aantal onder $H_{0}$ in de (1,1)-cel = 145 $\times$ 800/1372 = 84.55 ;
$E_{12}$ = het verwachte aantal onder $H_{0}$ in de (1,2)-cel = 145 $\times$ 572/1372 = 60.45 ;
$E_{21}$ = het verwachte aantal onder $H_{0}$ in de (2,1)-cel = 1227 $\times$ 800/1372 = 715.5 ;
$E_{22}$ = het verwachte aantal onder $H_{0}$ in de (2,2)-cel = 1227 $\times$ 572/1372 = 511.5 ;

Een toets van de nulhypothese gebeurt nu op basis van een vergelijking tussen de geobserveerde aantallen in cellen $(i, j),$ genoteerd met $O_{i j}$ en de verwachte aantallen $E_{i j}$ . In dat opzicht levert de toetsingsgrootheid

X^{2} = \frac{{(| O_{11} - E_{11} | - .5)}^{2}}{E_{11}} + \frac{{(| O_{12} - E_{12} | - .5)}^{2}}{E_{12}} + \frac{{(| O_{21} - E_{21} | - .5)}^{2}}{E_{21}} + \frac{{(| O_{22} - E_{22} | - .5)}^{2}}{E_{22}}

een goede discriminatie tussen de nulhypothese en de alternatieve hypothese. Men kan aantonen dat ze onder de nulhypothese bij benadering een zogenaamde $χ^{2}$ -verdeling volgt met 1 vrijheidsgraad. Deze verdeling neemt uiteraard alleen positieve waarden aan en is scheef naar rechts verdeeld, behalve als het aantal vrijheidsgraden groot is (minstens 100), in welk geval ze meer symmetrisch wordt.

Figuur 58 toont haar algemene vorm.

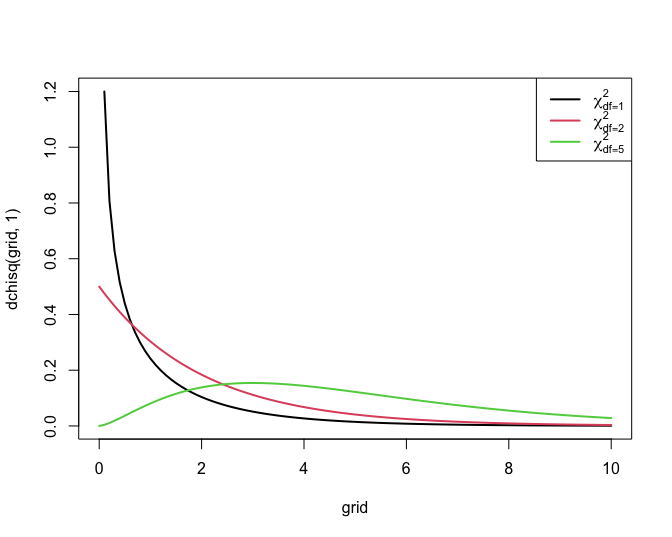
Figuur 58: Dichtheidsfuncties voor enkele Chi-kwadraat verdelingen

Een grote waarde van de toetsingsgrootheid geeft een indicatie van een afwijking van de nulhypothese. Concreet zal een toets op het $α 100 %$ significantieniveau de nulhypothese verwerpen zodra de geobserveerde waarde van de toetsingsgrootheid het $100 % (1 - α)$ -percentiel, $χ_{1, α}^{2}$ , van de $χ_{1}^{2}$ -verdeling overschrijdt. Ze kan niet verwerpen in het andere geval. De p-waarde voor een 2-zijdige toets is in dit geval de kans om een grotere waarde voor de toetsingsgrootheid te observeren dan de geobserveerde waarde $x^{2}$ als de nulhypothese waar is. Dit is de kans dat een $χ_{1}^{2}$ -verdeelde toevalsveranderlijke waarden groter dan $x^{2}$ aanneemt.

expected <- matrix(0, nrow = 2, ncol = 2)
for (i in 1:2)
    for (j in 1:2)
        expected[i,j] <- sum(brcaTab2[i,]) * sum(brcaTab2[,j]) / sum(brcaTab2)
expected

##          [,1]     [,2]
## [1,]  84.5481  60.4519
## [2,] 715.4519 511.5481

x2 <- sum((abs(brcaTab2 - expected) - .5)^2 / expected)
1-pchisq(x2, 1)

## [1] 0.481519

Omdat de observaties $O_{i j}$ in feite discrete getallen zijn, kan de toetsingsgrootheid $X^{2}$ slechts discrete waarden aannemen en kan een continue verdeling zoals de $χ_{1}^{2}$ -verdeling slechts een benadering zijn voor haar werkelijke verdeling. Om de discrete verdeling beter bij de continue $χ_{1}^{2}$ -verdeling te doen aansluiten, heeft men in de uitdrukking van de toetsingsgrootheid voor elke cel telkens 0.5 afgetrokken. Dit wordt een continuïteitscorrectie genoemd. In dit geval gaat het om de correctie van Yates en noemt men deze toets dan ook de Pearson Chi-kwadraat toets met Yates correctie. Wanneer de correctie niet gebruikt wordt (d.w.z. wanneer de getallen `0.5’ in de uitdrukking voor $X^{2}$ door 0 vervangen worden), dan spreekt men van de Pearson Chi-kwadraat toets. In R kan je deze toetsen uitvoeren door de optie op TRUE of FALSE te zetten:

chisq.test(brcaTab2)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  brcaTab2
## X-squared = 0.49542, df = 1, p-value = 0.4815

chisq.test(brcaTab2, correct = FALSE)

## 
##  Pearson's Chi-squared test
## 
## data:  brcaTab2
## X-squared = 0.62871, df = 1, p-value = 0.4278

Zelfs wanneer de continuïteitscorrectie wordt gebruikt, zal de $χ_{1}^{2}$ benadering voor de verdeling van de toetsingsgrootheid slechts verantwoord zijn als in geen enkele van de cellen het verwachte aantal onder $H_{0}$ kleiner is dan 5. Wanneer de $χ^{2}$ -benadering niet verantwoord is, kan men een exacte toets uitvoeren die rekening houdt met de echte mogelijke verdelingen van de marginale tellingen over de individuele cellen in de tabel. Dergelijke test maakt bijgevolg geen $χ^{2}$ -benadering voor de verdeling van de toetsingsgrootheid onder de nulhypothese. De test die met de exacte verdeling van de marginale tellingen over de individuele cellen rekening houdt, wordt in de literatuur Fisher’s exact test genoemd. De nulhypothese van deze test is eveneens dat $X$ en $Y$ onafhankelijk zijn, en de alternatieve hypothese dat $X$ en $Y$ afhankelijk zijn. Een nadeel van de exacte test, is dat ze conservatief is (d.w.z. dat ze een kleinere kans hebben op een Type I fout dan vooropgesteld, en bijgevolg een grotere kans op Type II fouten). In R bekomt men deze test als volgt:

fisher.test(brcaTab2)

## 
##  Fisher's Exact Test for Count Data
## 
## data:  brcaTab2
## p-value = 0.4764
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
##  0.7998798 1.6738449
## sample estimates:
## odds ratio 
##   1.153279

Merk op dat deze functie tevens 95% betrouwbaarheidsintervallen rapporteert voor de bijhorende odds ratio.