In zijn boek De blinde horlogemaker¹ (originele titel: The Blind Watchmaker) uit 1986 zegt Richard Dawkins:

I don't know who it was first pointed out that, given enough time, a monkey bashing away at random on a typewriter could produce all the works of Shakespeare. The operative phrase is, of course, given enough time. Let us limit the task facing our monkey somewhat. Suppose that he has to produce, not the complete works of Shakespeare but just the short sentence 'METHINKS IT IS LIKE A WEASEL', and we shall make it relatively easy by giving him a typewriter with a restricted keyboard, one with just the 26 (capital) letters, and a space bar. How long will he take to write this one little sentence?

Verderop argumenteert Dawkins dat dit een slechte analogie is voor evolutie, en stelt hij het volgende alternatief voor:

We again use our computer monkey, but with a crucial difference in its program. It again begins by choosing a random sequence of 28 letters, just as before … it duplicates it repeatedly, but with a certain chance of random error — 'mutation' — in the copying. The computer examines the mutant nonsense phrases, the 'progeny' of the original phrase, and chooses the one which, however slightly, most resembles the target phrase, 'METHINKS IT IS LIKE A WEASEL'.

Hij omschrijft daarna een computerprogramma waarmee hij zijn aap gesimuleerd heeft, en waarvan hij beweert dat het een half uur nodig had om tot de gewenste zin te komen omdat het geschreven was in de programmeertaal BASIC². Nadat hij zijn programma had herschreven in de programmeertaal Pascal³, duurde het nog slechts elf seconden om de gewenste zin te bekomen.

Dawkins liet echter na om de broncode van het computerprogramma in zijn boek op te nemen, noch om een formele omschrijving van het gebruikte algoritme te geven. Het boek bevat enkel de uitvoer van enkele simulatiestappen van het computerprogramma. Om het principe van evolutie te illustreren, vertrekt Dawkins vanaf de willekeurige zin

Y YVMQKZPFJXWVHGLAWFVCHQYOPY

Uit deze zin worden telkens nieuwe zinnen voortgebracht. Hierbij wordt de zin herhaaldelijk gedupliceerd, waarbij er een zekere kans is op een willekeurige fout — een mutatie — tijdens het kopieerproces. Na elke 10 generaties wordt het (beste) resultaat uitgeschreven:

Y YVMQKSPFTXWSHLIKEFV HQYSPY
YETHINKSPITXISHLIKEFA WQYSEY
METHINKS IT ISSLIKE A WEFSEY
METHINKS IT ISBLIKE A WEASES
METHINKS IT ISJLIKE A WEASEO
METHINKS IT IS LIKE A WEASEP

Op die manier werd de gewenste zin

METHINKS IT IS LIKE A WEASEL

bekomen na 64 generaties. Zonder een gedetailleerde omschrijving van het algoritme stond de procedure die gebruikt werd om de zinnen te genereren open voor heel wat verschillende interpretaties. De speculaties werden nog verder gevoed door een fragment in de BBC reeks die Richard Dawkins over zijn boek maakte, en waarin een simulatie van het programma op het scherm te zien is (zie onderstaande fragment vanaf 4:00).

Opgave

Wat Richard Dawkins in zijn boek omschrijft, is een voorloper van wat we vandaag een genetisch algoritme⁴ zouden noemen. Dit is een klasse van algoritmen die gebruikt worden om oplossingen te vinden voor optimalisatie- en zoekproblemen, waarbij uitgegaan wordt van ideeën uit de evolutietheorie zoals overerving, mutatie, natuurlijke selectie en crossover. Je opdracht bestaat erin enkele bouwstenen voor een genetisch algoritme te implementeren.

• Schrijf een functie fitness waaraan twee strings moeten doorgegeven worden. Indien de strings een verschillende lengte hebben, dan moet de functie een AssertionError opwerpen met de boodschap strings moeten even lang zijn. Anders moet de functie een natuurlijk getal teruggeven dat aangeeft op hoeveel posities eenzelfde karakter staat in de twee strings.

• Schrijf een functie mutatie waaraan een string moet doorgegeven worden. De functie heeft ook nog een tweede optionele parameter mutaties (standaardwaarde: 1) waaraan een getal $$m \in \mathbb{N}$$ kan doorgegeven worden. Als de gegeven string $$n \in \mathbb{N}$$ karakters lang is, dan moet de functie een string van $$n$$ hoofdletters en spaties teruggeven die in exact $$m$$ posities verschilt van de gegeven string. De gegeven string moet met andere woorden exact $$m$$ mutaties ondergaan hebben. Zorg ervoor dat elke positie van de gegeven string evenveel kans maakt om te muteren, en dat alle hoofdletters of de spatie evenveel kans maken om het karakter op een bepaalde positie te vervangen. Er moet uiteraard gelden dat $$0 \leq m \leq n$$. Indien dit niet het geval is, dan moet de functie een AssertionError opwerpen met de boodschap ongeldig aantal mutaties.

• Schrijf een functie crossover waaraan twee strings moeten doorgegeven worden. Indien de strings een verschillende lengte hebben, dan moet de functie een AssertionError opwerpen met de boodschap strings moeten even lang zijn. De functie heeft ook nog een derde optionele parameter punt, waaraan een getal $$c \in \mathbb{N}_0$$ kan doorgegeven worden. Als de gegeven strings beide $$n \in \mathbb{N}$$ karakters lang zijn, dan moet de functie een tuple van twee strings teruggeven die ontstaan na crossover van de gegeven strings met crossoverpunt op positie $$c$$. Deze crossoverprocedure wordt geïllustreerd in onderstaande figuur.

  

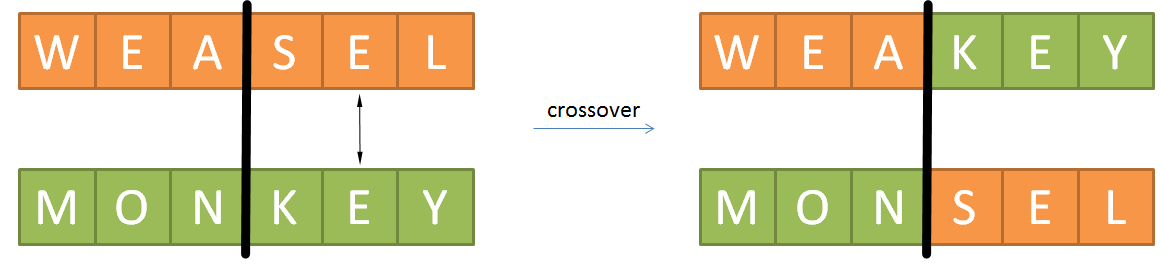
  We zetten de twee strings onder elkaar en trekken na $$c$$ karakters een verticale streep door de twee strings. De eerste string van het tuple wordt gevormd door het deel van de eerste gegeven string links van de streep, gevolgd door het deel van de tweede gegeven string rechts van de streep. De tweede string van het tuple wordt gevormd door het deel van de tweede gegeven string links van de streep, gevolgd door het deel van de eerste gegeven string rechts van de streep. Er moet gelden dat $$0 < c < n$$. Indien dit niet het geval is, dan moet de functie een AssertionError opwerpen met de boodschap ongeldig crossoverpunt. Indien er geen expliciete waarde wordt doorgegeven aan de parameter punt, dan moet een willekeurige waarde $$c \in \mathbb{N}_0$$ gekozen worden waarvoor geldt dat $$0 < c < n$$.

Je mag ervan uitgaan dat alle strings die als argument aan bovenstaande functies worden doorgegeven, enkel bestaan uit hoofdletters en spaties, en dat ze minstens twee karakters lang zijn. Deze voorwaarden hoef je dus niet expliciet te controleren.

Voorbeeld

>>> fitness('WEASEL', 'WETSEL')
5
>>> fitness('WEASEL', 'OECYEL')
3
>>> fitness('WEASEL', 'METHINKS')
Traceback (most recent call last):
AssertionError: strings moeten even lang zijn

>>> mutatie('WEASEL')
'WETSEL'
>>> mutatie('WEASEL', mutaties=3)
'OECYEL'
>>> mutatie('WEASEL', mutaties=13)
Traceback (most recent call last):
AssertionError: ongeldig aantal mutaties

>>> crossover('WEASEL', 'MONKEY', punt=3)
('WEAKEY', 'MONSEL')
>>> crossover('METHINKS', 'AARDVARK')
('MARDVARK', 'AETHINKS')
>>> crossover('WEASEL', 'METHINKS')
Traceback (most recent call last):
AssertionError: strings moeten even lang zijn
>>> crossover('WEASEL', 'MONKEY', punt=0)
Traceback (most recent call last):
AssertionError: ongeldig crossoverpunt
>>> crossover('WEASEL', 'MONKEY', punt=6)
Traceback (most recent call last):
AssertionError: ongeldig crossoverpunt