Je hebt drie proefbuizen met een maximale capaciteit van 3, 5 en 8 eenheden. De eerste twee proefbuizen zijn helemaal leeg en de derde is tot de rand gevuld met een vloeistof.
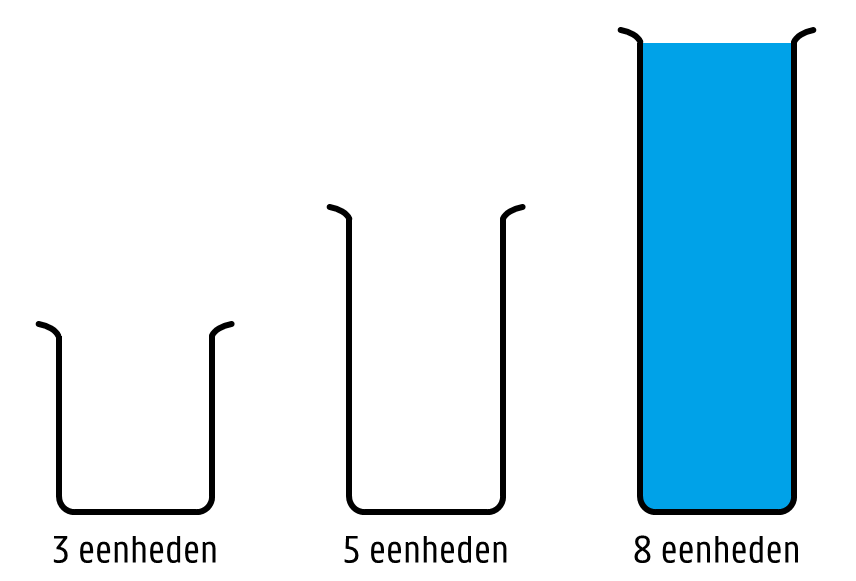
De proefbuizen hebben geen markeringen, waardoor het onmogelijk is om een exacte hoeveelheid vloeistof af te meten met een proefbuis die niet volledig vol is. Hoe kan je zonder morsen en in zo weinig mogelijk stappen exact 4 eenheden vloeistof afmeten als je in elke stap vloeistof kan gieten van een proefbuis (de bron) in een andere proefbuis (het doel) en daarbij maar mag stoppen bij welke van deze twee gevallen eerst gebeurt: de bron is leeg of het doel is vol?
Onderstaand schema geeft aan hoe je in 6 stappen exact 4 eenheden vloeistof kunt afmeten. Dit is ook het kleinste aantal stappen waarin dit kan, maar er zijn wel nog andere mogelijkheden om in 6 stappen exact 4 eenheden af te meten.
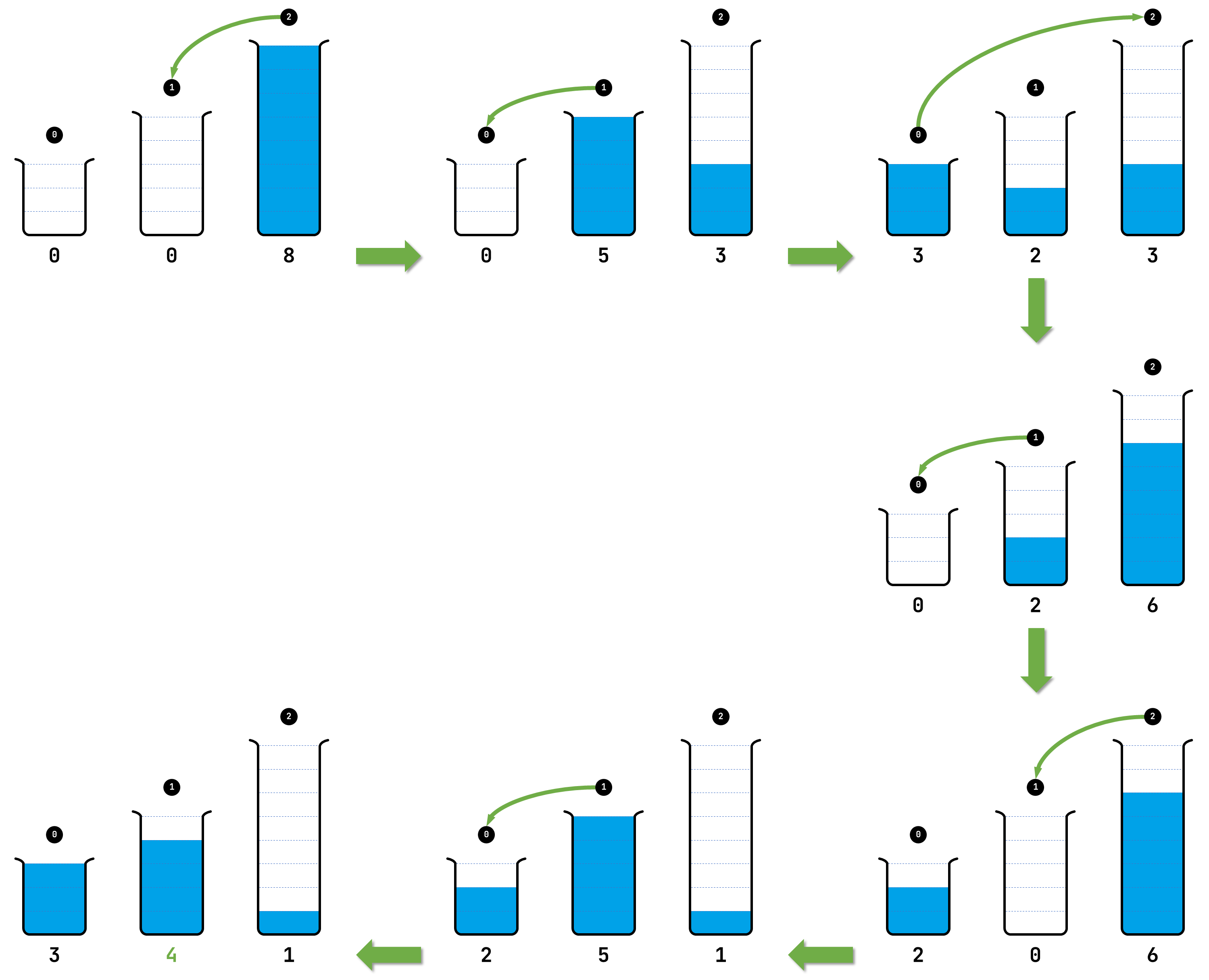
We hebben markeringen aangebracht om te tonen dat elke proefbuis in elke stap een geheel aantal eenheden vloeistof bevat. De dunne groene pijlen wijzen voor elke stap van de bron naar het doel.
Opgave
Dit raadsel kan veralgemeend worden naar $$n \in \mathbb{N}_0$$ proefbuizen, die we van links naar rechts nummeren vanaf nul. De capaciteit van de proefbuizen wordt beschreven door een tuple $$(c_0, c_1, \ldots, c_{n-1})$$, waarbij proefbuis $$i$$ maximaal $$c_i \in \mathbb{N}_0$$ (int) eenheden vloeistof kan bevatten ($$0 \leq i < n$$). De toestand van de proefbuizen op een bepaald moment wordt beschreven door een tuple $$(v_0, v_1, \ldots, v_{n-1})$$, waarbij proefbuis $$i$$ momenteel $$v_i \in \mathbb{N}$$ (int; $$0 \leq v_i \leq c_i$$) eenheden vloeistof bevat ($$0 \leq i < n$$). De capaciteit wordt dus beschreven als een toestand waarbij alle proefbuizen volledig gevuld zijn.
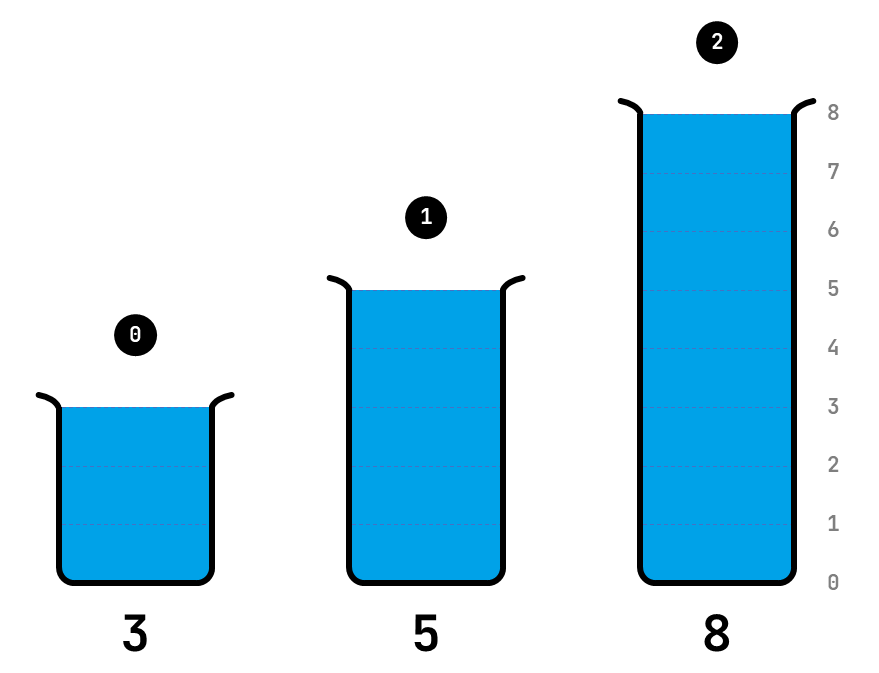
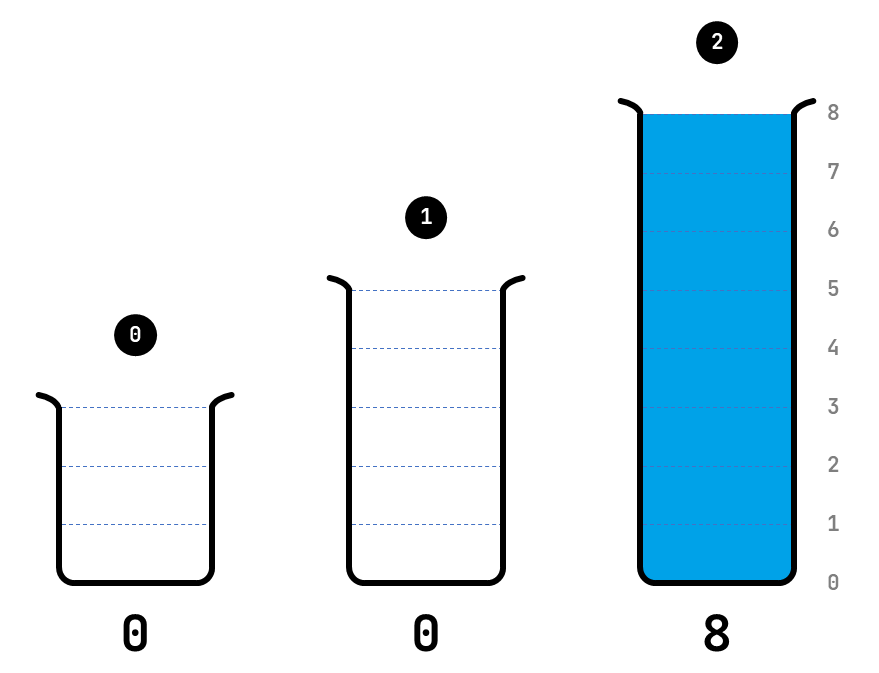
De drie proefbuizen uit de inleiding hebben capaciteit $$(3, 5, 8)$$ en bevinden zich initieel in toestand $$(0, 0, 8)$$.
Er bestaat een standaardprocedure om een oplossing van dit veralgemeend raadsel te vinden — als er een oplossing bestaat. Die procedure houdt een wachtrij $$Q$$ bij met toestanden die nog moeten verwerkt worden en ook de voorgangers van alle toestanden die ooit aan wachtrij $$Q$$ toegevoegd werden. Wachtrij $$Q$$ is een lijst (list) die initieel enkel de begintoestand bevat. De voorgangers houden we bij in een dictionary $$P$$ (dict) die toestanden afbeeldt op hun vorige toestand. Initieel beeldt dictionary $$P$$ enkel de begintoestand af op de waarde None, om aan te geven dat de begintoestand geen voorganger heeft.
Elke stap van de procedure verwerkt toestand $$p$$ aan het begin van wachtrij $$Q$$. Eerst wordt toestand $$p$$ aan het begin van wachtrij $$Q$$ verwijderd. Daarna worden alle mogelijke toestanden bepaald die kunnen volgen op toestand $$p$$. Een volgende toestand wordt bekomen door vloeistof te gieten van proefbuis $$x$$ (de bron) in proefbuis $$y$$ (het doel). Dit kan enkel als i) de bron $$x$$ en het doel $$y$$ verschillende proefbuizen zijn, ii) de bron $$x$$ niet leeg is, en iii) het doel $$y$$ niet vol is.
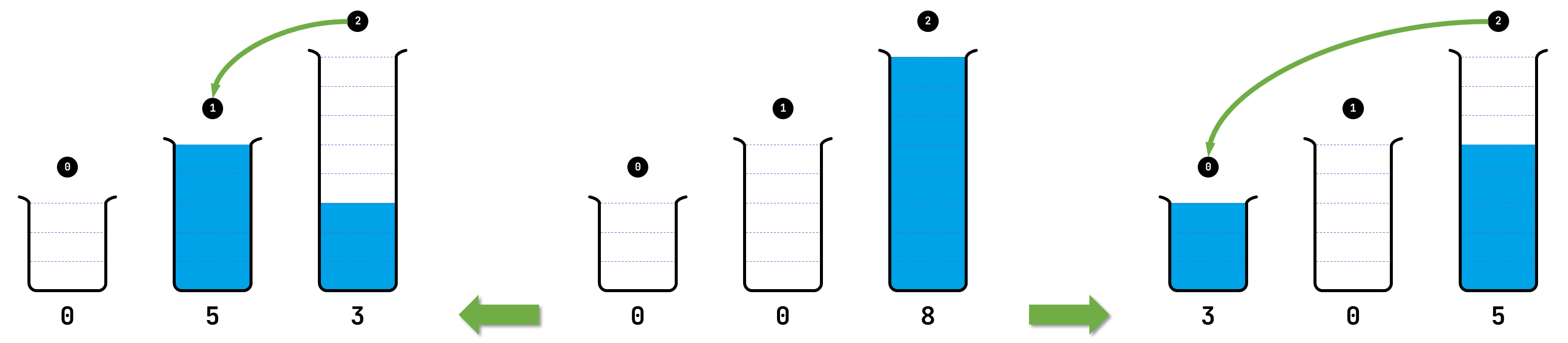
Onderstaande figuur illustreert dat de begintoestand $$(0, 0, 8)$$ van het raadsel uit de inleiding kan gevolgd worden door toestanden $$(0, 5, 3)$$ en $$(3, 0, 5)$$. Aan de linkerkant geeft de dunne groene pijl aan dat toestand $$(0, 5, 3)$$ volgt na toestand $$(0, 0, 8)$$ door vloeistof te gieten van proefbuis 2 in proefbuis 1. Aan de rechterkant geeft de dunne groene pijl aan dat toestand $$(3, 0, 5)$$ volgt na toestand $$(0, 0, 8)$$ door vloeistof te gieten van proefbuis 2 in proefbuis 0. Voor alle andere combinaties van een bron en een doel kan er niet gegoten worden in toestand $$(0, 0, 8)$$.
Ten slotte worden alle volgende toestanden van $$p$$ van klein naar groot verwerkt: die volgorde wordt bepaald door eerst de hoeveelheid vloeistof in de proefbuizen op positie $$0$$ te vergelijken, en zolang de proefbuizen op positie $$x$$ dezelfde hoeveelheid vloeistof bevatten vervolgens de hoeveelheid in de proefbuizen op positie $$x + 1$$ te vergelijken. Voor elke volgende toestand $$s$$ die nooit eerder aan wachtrij $$Q$$ toegevoegd werd, voegen we $$s$$ achteraan toe aan de wachtrij en onthouden we dat $$s$$ volgt op toestand $$p$$ door $$s$$ af te beelden op $$p$$ in dictionary $$P$$.
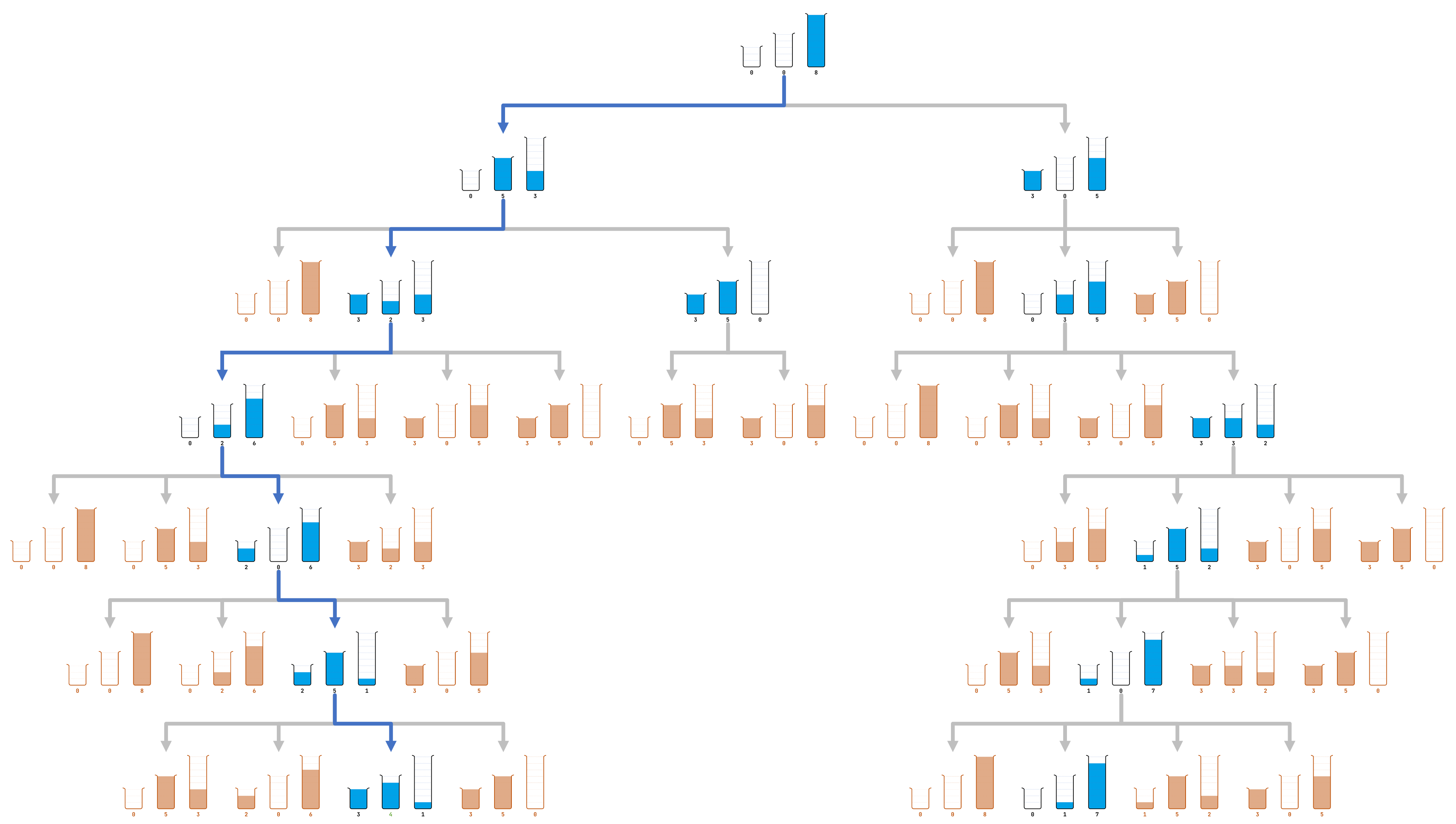
Hieronder tonen we hoe deze procedure verloopt voor het raadsel uit de inleiding. De begintoestand $$(0, 0, 8)$$ staat aan de bovenkant van de boomstructuur. Elke toestand is met pijlen verbonden met alle mogelijke toestanden die erop kunnen volgen. Die pijlen worden in dictionary $$P$$ bijgehouden. De volgorde waarin de toestanden aan wachtrij $$Q$$ toegevoegd en er ook weer uitgehaald worden, bekom je door de blauwe toestanden in de boomstructuur af te lopen in de gebruikelijke leesvolgorde: van links naar rechts en van boven naar onder. De volgende toestanden die niet verder verwerkt worden — en dus niet opnieuw aan wachtrij $$Q$$ toegevoegd worden — zijn oranje gekleurd in de boomstructuur.
Voor het raadsel uit de inleiding bevat onderstaande tabel voor de opeenvolgende stappen die de procedure doorloopt i) de toestand die moet verwerkt worden, ii) de toestanden die daarop kunnen volgen, en iii) de acties die moeten uitgevoerd worden op de wachtrij. De volgende toestanden die niet moeten verwerkt worden omdat ze in een vorige stap al eens aan de wachtrij werden toegevoegd, zijn oranje gekleurd. De toestanden die aan het begin van de wachtrij weggehaald worden, zijn doorgehaald en rood gekleurd. De toestanden die achteraan de wachtrij toegevoegd worden, zijn groen gekleurd.
| toestand | volgende toestanden | wachtrij |
|---|---|---|
| - | - | (0, 0, 8) |
| (0, 0, 8) | (0, 5, 3) (3, 0, 5) | (0, 0, 8) (0, 5, 3) (3, 0, 5) |
| (0, 5, 3) | (0, 0, 8) (3, 2, 3) (3, 5, 0) | (0, 5, 3) (3, 0, 5) (3, 2, 3) (3, 5, 0) |
| (3, 0, 5) | (0, 0, 8) (0, 3, 5) (3, 5, 0) | (3, 0, 5) (3, 2, 3) (3, 5, 0) (0, 3, 5) |
| (3, 2, 3) | (0, 2, 6) (0, 5, 3) (3, 0, 5) (3, 5, 0) | (3, 2, 3) (3, 5, 0) (0, 3, 5) (0, 2, 6) |
| (3, 5, 0) | (0, 5, 3) (3, 0, 5) | (3, 5, 0) (0, 3, 5) (0, 2, 6) |
| (0, 3, 5) | (0, 0, 8) (0, 5, 3) (3, 0, 5) (3, 3, 2) | (0, 3, 5) (0, 2, 6) (3, 3, 2) |
| (0, 2, 6) | (0, 0, 8) (0, 5, 3) (2, 0, 6) (3, 2, 3) | (0, 2, 6) (3, 3, 2) (2, 0, 6) |
| (3, 3, 2) | (0, 3, 5) (1, 5, 2) (3, 0, 5) (3, 5, 0) | (3, 3, 2) (2, 0, 6) (1, 5, 2) |
| (2, 0, 6) | (0, 0, 8) (0, 2, 6) (2, 5, 1) (3, 0, 5) | (2, 0, 6) (1, 5, 2) (2, 5, 1) |
| (1, 5, 2) | (0, 5, 3) (1, 0, 7) (3, 3, 2) (3, 5, 0) | (1, 5, 2) (2, 5, 1) (1, 0, 7) |
| (2, 5, 1) | (0, 5, 3) (2, 0, 6) (3, 4, 1) (3, 5, 0) | (2, 5, 1) (1, 0, 7) (3, 4, 1) |
| (1, 0, 7) | (0, 0, 8) (0, 1, 7) (1, 5, 2) (3, 0, 5) | (1, 0, 7) (3, 4, 1) (0, 1, 7) |
Er zijn twee mogelijke gevallen waarbij de procedure stopt. Als wachtrij $$Q$$ geen toestanden meer bevat, dan kunnen we geen stap meer zetten en besluiten dat de gevraagde hoeveelheid vloeistof niet kan afgemeten worden. Als toestand $$p$$ aan het begin van wachtrij $$Q$$ een proefbuis heeft die de gevraagde hoeveelheid vloeistof bevat, dan kunnen we dictionary $$P$$ gebruiken om (achterwaarts) de route te reconstrueren vanaf de begintoestand tot toestand $$p$$. Deze route beschrijft hoe we met zo weinig mogelijk keer gieten de gevraagde hoeveelheid vloeistof kunnen afmeten, en is dus een oplossing voor het raadsel.
Voor het raadsel uit de inleiding zien we in bovenstaande figuur dat toestand $$(3, 4, 1)$$ de eerste toestand aan het begin van de wachtrij is met een proefbuis die 4 eenheden vloeistof bevat. De blauwe pijlen tonen de route van begintoestand $$(0, 0, 8)$$ naar toestand $$(3, 4, 1)$$ die de oplossing van het raadsel beschrijft die door de standaardprocedure wordt gevonden: \[ (0, 0, 8) \longrightarrow (0, 5, 3) \longrightarrow (3, 2, 3) \longrightarrow (0, 2, 6) \longrightarrow (2, 0, 6) \longrightarrow (2, 5, 1) \longrightarrow (3, 4, 1)\]
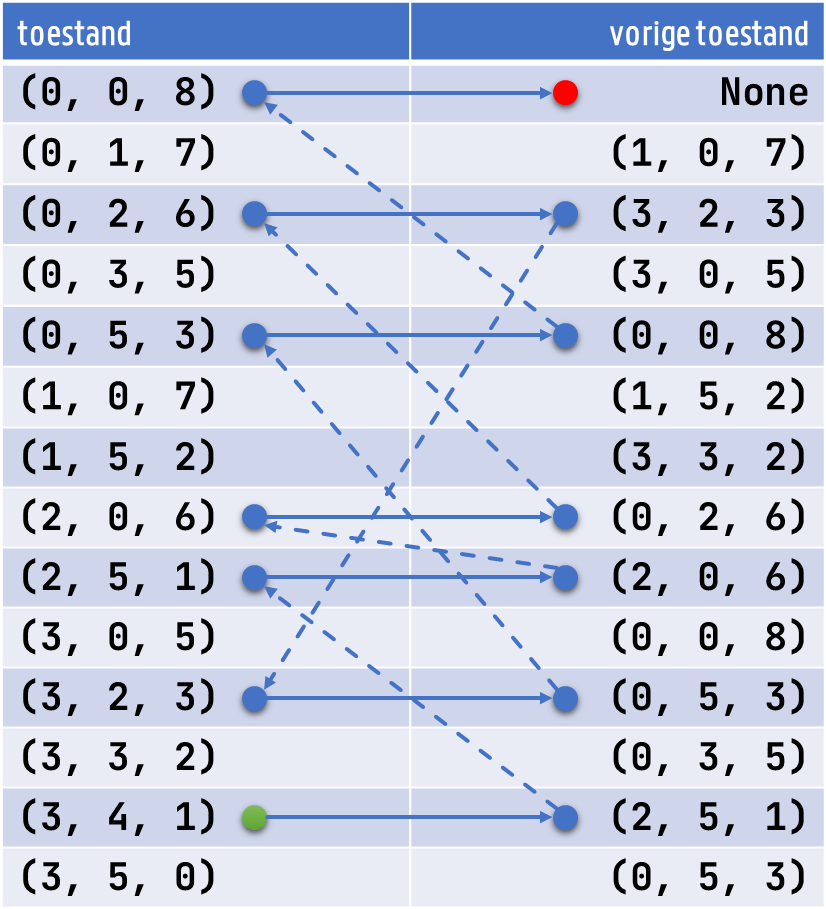
Dit is de inhoud van dictionary $$P$$ op het moment dat toestand $$(3, 4, 1)$$ op kop van de wachtrij staat bij het uitvoeren van de standaardprocedure voor het raadsel uit de inleiding. De blauwe pijlen geven aan hoe de route van begintoestand $$(0, 0, 8)$$ naar toestand $$(3, 4, 1)$$ achterwaarts kan gereconstrueerd worden door te beginnen bij toestand $$(3, 4, 1)$$ (groene cirkel) en telkens de vorige toestand op te zoeken tot aan de begintoestand die geen vorige toestand meer heeft (rode cirkel).
Gevraagd wordt:
-
Schrijf een functie gieten waaraan vier argumenten moeten doorgegeven worden: i) een toestand $$p$$ van proefbuizen, ii) de capaciteit $$c$$ van de proefbuizen, iii) het volgnummer $$x$$ van een proefbuis (de bron) en iv) het volgnummer $$y$$ van een proefbuis (het doel). Als het in toestand $$p$$ niet mogelijk is om vloeistof te gieten van bron $$x$$ in doel $$y$$, dan moet de waarde None teruggegeven worden. Anders moet de toestand van de proefbuizen teruggegeven worden nadat in toestand $$p$$ vloeistof werd gegoten van bron $$x$$ in doel $$y$$, waarbij pas gestopt werd als de bron leeg was of als het doel was vol was (zijnde welk van deze twee gevallen eerst gebeurde).
-
Schrijf een functie volgende_toestanden waaraan een toestand $$p$$ van proefbuizen en de capaciteit $$c$$ van de proefbuizen moeten doorgegeven worden. De functie moet een verzameling (set) doorgeven met alle mogelijke toestanden van de proefbuizen die na één keer gieten kunnen volgen op toestand $$p$$.
-
Schrijf een functie stap waaraan drie argumenten moeten doorgegeven worden: i) een wachtrij $$Q$$ (list), ii) een dictionary $$P$$ (dict) met voorgangers en iii) de capaciteit $$c$$ van de proefbuizen. De inhoud van wachtrij $$Q$$ en dictionary $$P$$ beschrijft een moment tijdens de procedure om het raadsel op te lossen. Daarbij mag ervan uitgaan worden dat wachtrij $$Q$$ niet leeg is, zonder dat dit expliciet moet gecontroleerd worden. De functie moet één stap uit de procedure uitvoeren, waarbij toestand $$p$$ aan het begin van wachtrij $$Q$$ weggehaald wordt en alle volgende toestanden van $$p$$ verwerkt worden zoals voorgeschreven door de procedure. Bij het uitvoeren van die stap moeten wachtrij $$Q$$ en dictionary $$P$$ indien nodig bijgewerkt worden. De functie moet niet expliciet iets teruggeven (lees: moet de waarde None teruggeven).
-
Schrijf een functie route waaraan een toestand $$p$$ van proefbuizen en een dictionary $$P$$ (dict) met voorgangers moeten doorgegeven worden. Daarbij beschrijft dictionary $$P$$ de voorgangers op een moment tijdens de procedure om een raadsel op te lossen en is toestand $$p$$ op dat moment eerder al aan de wachtrij toegevoegd. De functie moet een lijst (list) met toestanden teruggeven die de route beschrijft van de begintoestand van het raadsel tot toestand $$p$$, die uit dictionary $$P$$ kan gereconstrueerd worden. De dictionary $$P$$ met voorgangers mag door de functie niet gewijzigd worden.
-
Schrijf een functie oplossing waaraan drie argumenten moeten doorgegeven worden die een veralgemeend raadsel met proefbuizen beschrijven: i) de begintoestand $$p$$ van de proefbuizen, ii) de capaciteit $$c$$ van de proefbuizen en iii) een gevraagde hoeveelheid vloeistof $$v \in \mathbb{N}_0$$ (int). Als het raadsel geen oplossing heeft, dan moet de waarde None teruggegeven worden. Anders moet de functie de oplossing van het raadsel teruggeven die met de standaardprocedure gevonden wordt, voorgesteld als een lijst (list) van toestanden die een kortste route van opeenvolgende toestanden beschrijft.
Al deze functies mogen ervan uitgaan dat de argumenten die eraan doorgegeven worden geldig zijn, zonder dat dit expliciet moet gecontroleerd worden.
Voorbeeld
>>> gieten((0, 2, 6), (3, 5, 8), 2, 0)
(3, 2, 3)
>>> gieten((0, 2, 6), (3, 5, 8), 2, 1)
(0, 5, 3)
>>> gieten((3, 2, 3), (3, 5, 8), 1, 0)
>>> gieten((3, 2, 3), (3, 5, 8), 2, 2)
>>> volgende_toestanden((0, 0, 8), (3, 5, 8))
{(0, 5, 3), (3, 0, 5)}
>>> volgende_toestanden((0, 5, 3), (3, 5, 8))
{(3, 2, 3), (0, 0, 8), (3, 5, 0)}
>>> volgende_toestanden((3, 0, 5), (3, 5, 8))
{(0, 3, 5), (0, 0, 8), (3, 5, 0)}
>>> wachtrij = [(0, 0, 8)]
>>> voorganger = {(0, 0, 8): None}
>>> stap(wachtrij, voorganger, (3, 5, 8))
>>> wachtrij
[(0, 5, 3), (3, 0, 5)]
>>> voorganger
{(0, 0, 8): None, (0, 5, 3): (0, 0, 8), (3, 0, 5): (0, 0, 8)}
>>> stap(wachtrij, voorganger, (3, 5, 8))
>>> wachtrij
[(3, 0, 5), (3, 2, 3), (3, 5, 0)]
>>> voorganger
{(0, 0, 8): None, (0, 5, 3): (0, 0, 8), (3, 0, 5): (0, 0, 8), (3, 2, 3): (0, 5, 3), (3, 5, 0): (0, 5, 3)}
>>> route((3, 5, 0), voorganger)
[(0, 0, 8), (0, 5, 3), (3, 5, 0)]
>>> oplossing((0, 0, 8), (3, 5, 8), 4)
[(0, 0, 8), (0, 5, 3), (3, 2, 3), (0, 2, 6), (2, 0, 6), (2, 5, 1), (3, 4, 1)]
>>> oplossing((0, 5, 0, 17), (3, 5, 11, 17), 7)
[(0, 5, 0, 17), (0, 0, 5, 17), (0, 5, 5, 12), (0, 0, 10, 12), (0, 5, 10, 7)]
>>> oplossing((0, 0, 0, 0, 13), (5, 7, 7, 11, 13), 12)
[(0, 0, 0, 0, 13), (0, 0, 0, 11, 2), (5, 0, 0, 6, 2), (0, 0, 0, 6, 7), (5, 0, 0, 1, 7), (0, 0, 0, 1, 12)]