Een boek van kaft tot kaft doorlezen, beginnend bij de eerste bladzijde, omslaan, volgende bladzijde en zo verder tot de laatste bladzijde — dat is werkelijk niet meer van deze tijd. In plaats daarvan vatten we het paginanummer op als hyperlink: als we pagina 14 uit hebben, bladeren we 14 pagina's verder en lezen daar door.

In een boek met ouderwetse paginanummering zouden we dus van pagina 14 naar pagina 28 springen. Als een hyperlink de laatste pagina voorbijschiet, gaan we terug naar pagina 1 en tellen daar door. Dus als een boek 100 pagina's heeft, en we hebben pagina 74 uit, dan tellen we 26 pagina's door tot pagina 100, gaan bij pagina 1 verder en komen uit bij pagina 48 (want $$26 + 48 = 74$$). Let wel: zodra je op de laatste pagina komt (in dit geval pagina 100) is het uit met de pret, want die hyperlinkt per definitie naar zichzelf. Aangezien het zapleestraject van begin tot eind vastligt, is de enige vrijheidsgraad het aantal pagina's $$n$$. De vraag die zich dan stelt is of er waarden van $$n$$ zijn die een boek volledig zapleesbaar maken? Dat wil zeggen: geen enkele pagina blijft ongelezen.

Vervolgens stappen we af van de ouderwetse paginanummering. We mogen nu de paginanummers $$1, 2, \ldots, n$$ willekeurig over de $$n$$ pagina's verdelen. Het nummer dat op een pagina staat — bijvoorbeeld pagina 17 — is dan nog steeds een hyperlink. Je bladert dus na lezing 17 pagina's door. Maar dat zegt niets over het nummer van de pagina waarop je dan terechtkomt, want dat kan elk getal van 1 tot en met $$n$$ zijn. De vraag is dan voor welke waarden van $$n$$ en een gunstig gekozen volgorde van de paginanummers er boeken zijn die volledig zapleesbaar zijn? Alvast een voorschotje: voor een boek met 8 pagina's zijn er twee nummeringen mogelijk.

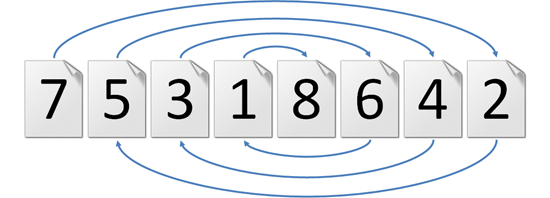
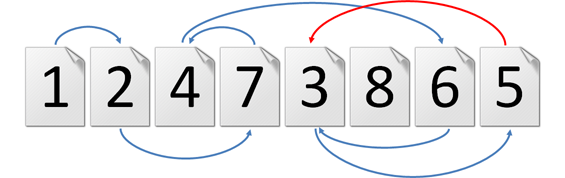
Opgave

Er kan aangetoond worden dat bij een ouderwetse paginanummering enkel de boeken met 1 en 2 pagina's zapleesbaar zijn. Bij boeken waarbij de paginanummering een permutatie vormt van de nummers $$1, 2, \ldots, n$$ hebben alle zapleesbare boeken steeds een even aantal pagina's $$n$$ als $$n > 1$$.

Voor een even aantal pagina's $$n$$ kan men een boek zapleesbaar maken door de paginanummers $$n-1, n-3, n-5, \ldots, 1$$ toe te kennen aan de pagina's op posities $$1, 2, \ldots, \frac{n}{2}$$, en door de paginanummers $$n, n-2, n-4, \ldots, 2$$ toe te kennen aan de pagina's $$\frac{n}{2}+1, \frac{n}{2}+2, \ldots, n$$.

Als het aantal pagina's $$n$$ een macht van twee is — met andere woorden als $$n = 2^m$$ voor een $$m \in \mathbb{N}$$ — dan bestaat er een tweede constructiemethode om het boek zapleesbaar te maken. Bij deze methode krijgt pagina 1 het paginanummer 1, en krijgt elke volgende pagina die je leest in zapleesvolgorde steeds één paginanummer hoger dan deze van de pagina die daarvoor werd gelezen.

Gevraagd wordt:

• Schrijf een functie iszapleesbaar waaraan een lijst (list) met $$n \in \mathbb{N}$$ paginanummers (int) moet doorgegeven worden. De functie moet een Booleaanse waarde (bool) teruggeven die aangeeft of een boek met deze paginanummering zapleesbaar is. Dat is het geval als de paginanummers een permutatie vormen van de getallen $$1, 2, \ldots, n$$ en als je bij het zaplezen (vertrekkend vanaf de eerste pagina) alle pagina's te lezen krijgt.

• Schrijf een functie zapboek waaraan het aantal pagina's $$n \in \mathbb{N}_0$$ (int) van een boek moet doorgegeven worden. De functie moet een lijst (list) met paginanummers (int) teruggeven die het boek zapleesbaar maakt. Voor een even aantal paginanummers of voor $$n=1$$ moet de eerste constructiemethode gebruikt worden. Als $$n$$ echter een macht van twee is, dan moet de lijst van paginanummers opgebouwd worden volgens de tweede constructiemethode die hierboven beschreven werd. Voor een oneven aantal paginanummers $$n > 1$$ moet een lege lijst als resultaat teruggegeven worden, omdat er in dat geval geen zapleesbaar boek kan geconstrueerd worden.

Voorbeeld

>>> iszapleesbaar([7, 5, 3, 1, 8, 6, 4, 2])
True
>>> iszapleesbaar([1, 2, 4, 7, 3, 8, 6, 5])
False
>>> iszapleesbaar([1, 2, 5, 3, 8, 7, 4, 6])
True
>>> iszapleesbaar([1, 1, 1, 1, 1, 1, 1, 1])
False

>>> zapboek(6)
[5, 3, 1, 6, 4, 2]
>>> zapboek(7)
[]
>>> zapboek(8)
[1, 2, 5, 3, 8, 7, 4, 6]