Als één van de laatste stappen van genetische recombinatie kunnen twee homologe chromosomen tijdens de meiose genetisch materiaal uitwisselen in een proces dat synapsis genoemd wordt. Door deze chromosomale crossover ontstaan gerecombineerde chromosomen. Crossover komt meestal voor wanneer overeenkomstige regio's van overeenkomstige chromosomen breken en zich daarna terug aanhechten aan het andere chromosoom.
Een theoretische beschrijving van crossover werd geïntroduceerd door Thomas Hunt Morgan, die zich daarbij liet inspireren op het werk van de Belgische professor Frans Alfons Janssens van de Katholieke Universiteit Leuven. Deze laatste had het fenomeen reeds in 1909 beschreven en noemde het chiasmatypie.
Opgave
In deze opgave stellen we een chromosoom voor als een lijst of een tuple van strikt stijgende gehele getallen (elk getal is dus groter dan het voorgaande getal). De punten waar twee chromosomen kunnen openbreken — en waar zich dus crossover kan voordoen — worden aangegeven door de gemeenschappelijke getallen in de twee corresponderende lijsten of tuples. Dit wordt geïllustreerd in onderstaande afbeelding, waarbij crossover kan voorkomen waar de twee chromosomen elkaar raken.
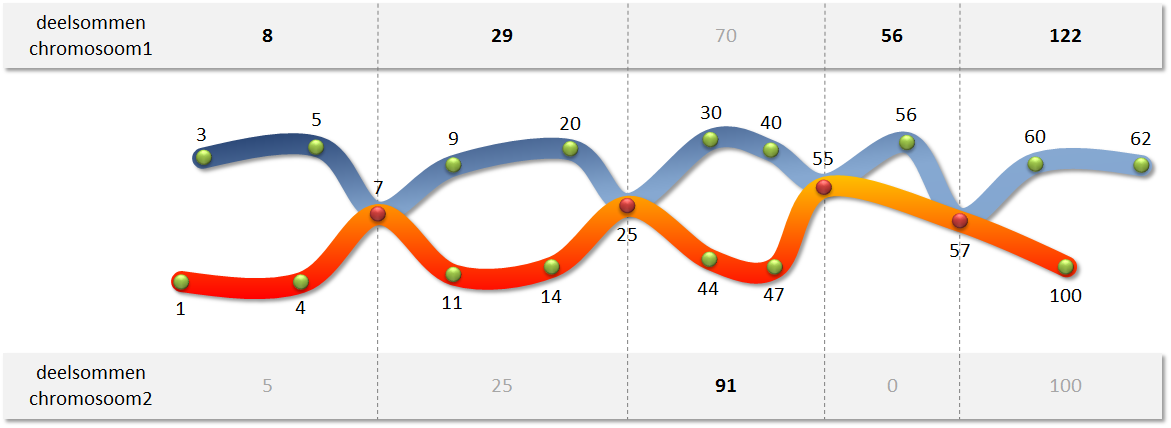
De chromosomen kunnen op de volgende manier doorlopen worden:
-
Als startpunt kan het begin (de linkerkant) van één van beide chromosomen gekozen worden.
-
Vanaf elk punt kan vooruit (naar rechts) gestapt worden.
-
Bij een crossoverpunt heb je de keuze om verder te stappen op hetzelfde chromosoom, of over te schakelen op het andere chromosoom.
Gevraagd wordt:
-
Schrijf een functie crossoverpunten waaraan twee chromosomen moeten doorgegeven worden. De functie moet teruggeven hoeveel crossoverpunten er zijn tussen deze chromosomen.
-
Schrijf een functie maximaleSom waaraan twee chromosomen moeten doorgegeven worden. De functie moet de maximale som bepalen van alle paden die op de hierboven beschreven manier kunnen doorlopen worden. In het bovenstaand voorbeeld wordt de maximale som 450 bereikt door het volgende pad te doorlopen:
3 + 5 + 7 + 9 + 20 + 25 + 44 + 47 + 55 + 56 + 57 + 60 + 62De maximale som wordt gevonden door de maximale deelsommen te bepalen van de fragmenten vóór het eerste crossoverpunt, tussen opeenvolgende crossoverpunten, en na het laatste crossoverpunt. Merk op dat het mogelijk is dat twee deelsommen gelijk zijn indien de eindpunten zelf crossoverpunten zijn, of indien twee crossoverpunten elkaar onmiddellijk opvolgen zonder tussenliggende punten.
Algoritme
Om de crossoverpunten te vinden, kan je gebruikmaken van het feit dat de getallen in de twee gegeven lijsten strikt stijgend zijn. Je kunt beide lijsten dan tegelijkertijd van links naar rechts doorlopen, waarbij je voor elke lijst afzonderlijk bijhoudt op welke positie je je momenteel bevindt. Ga telkens één stap vooruit in de lijst waar op de huidige positie het kleinste getal staat. Als je op de huidige positie in beide lijsten eenzelfde getal aantreft, dan heb je een crossoverpunt gevonden. Tijdens het doorlopen van beide lijsten kan je meteen ook al de deelsommen voor, tussen, en na de crossoverpunten bepalen.
Voorbeeld
>>> chromosoom1 = [3, 5, 7, 9, 20, 25, 30, 40, 55, 56, 57, 60, 62]
>>> chromosoom2 = [1, 4, 7, 11, 14, 25, 44, 47, 55, 57, 100]
>>> crossoverpunten(chromosoom1, chromosoom2)
4
>>> maximaleSom(chromosoom1, chromosoom2)
450
>>> chromosoom1 = [-5, 100, 1000, 1005]
>>> chromosoom2 = [-12, 1000, 1001]
>>> crossoverpunten(chromosoom1, chromosoom2)
1
>>> maximaleSom(chromosoom1, chromosoom2)
2100