Een telecommunicatiebedrijf wil bij het uitbouwen van een netwerk voor mobiele telefonie een aantal zendmasten neerplanten. Het wil de zendmasten op zo een manier plaatsen, dat de gemiddelde ontvangstkwaliteit over een reeks van ontvangstpunten zo groot mogelijk is.

Als een signaal wordt uitgezonden door een zendmast met coördinaten $$(x_z, y_z)$$, dan gaan we er voor deze opgave van uit dat de ontvangstkwaliteit $$s \in [0, 1]$$ in een ontvangstpunt met coördinaten $$(x_o, y_o)$$ enkel afhangt van de afstand $$r$$ tussen het ontvangstpunt en de zendmasten, en van een parameter $$\alpha$$ die de sterkte van de zendmasten aangeeft. Daarbij wordt de afstand gegeven door \[r = \sqrt{(x_o - x_z)^2 + (y_o - y_z)^2}\] We gaan er voor de eenvoud ook van uit dat alle zendmasten eenzelfde sterkte hebben. Elk model van zendmast kan daardoor omschreven worden door een signaalfunctie $$f(r, \alpha)$$. Deze functie neemt voor een punt op een gegeven afstand tot de zendmast een waarde tussen 0 en 1 aan die de ontvangststerkte aangeeft.

Verschillende functies die de ontvangststerkte $$s$$ van het signaal van een zendmast uitdrukken in functie van de afstand $$r$$ tot de zendmast, en dit voor zendmasten met sterkte $$\alpha = 2$$.

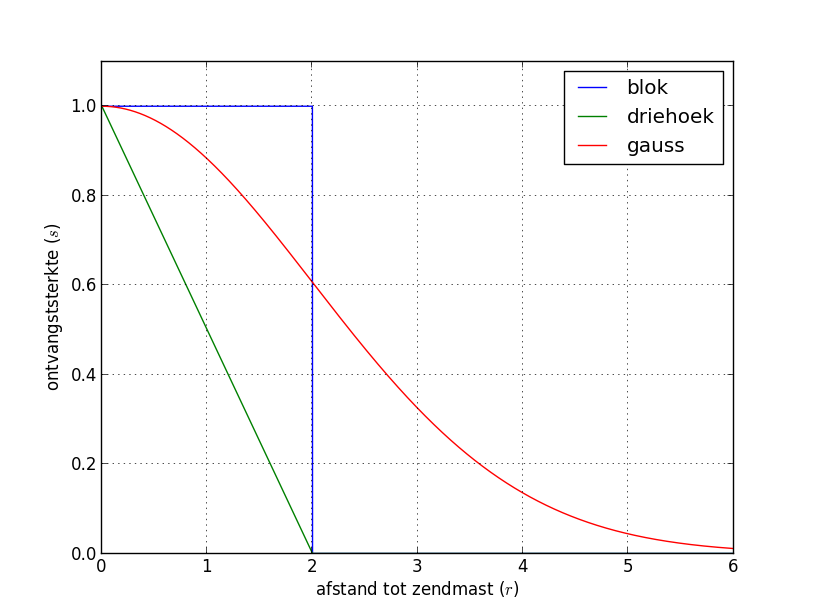
Bovenstaande figuur toont het verloop van de ontvangststerkte $$s$$ voor een aantal modellen van zendmasten, in functie van de afstand $$r$$ tot de zendmast:

blokvormige sterkte (blok): alle punten binnen straal $$\alpha$$ (inclusief de punten op de rand) hebben ontvangststerkte 1, en de punten daarbuiten hebben ontvangststerkte 0
driehoeksvormige sterkte (driehoek): de ontvangststerkte neemt lineair af van 1 op het punt van de zendmast tot 0 voor punten op afstand $$\alpha$$ van de zendmast; punten met een afstand groter dan $$\alpha$$ tot de zendmast hebben ook ontvangststerkte 0
sterkte volgens Gausscurve (gauss): de ontvangststerkte wordt gegeven door $$e^{\frac{-r^2}{2\alpha^2}}$$

Als een ontvangstpunt signalen ontvangt van meerdere zendmasten, dan is de ontvangststerkte op dat punt gelijk aan de maximale ontvangststerkte van de signalen van de individuele zendmasten.

Voorbereiding

In Python zijn functies zelf ook objecten, waardoor je ze kunt gebruiken zoals alle andere objecten. In het bijzonder kun je functies toekennen aan variabelen of doorgeven als argument aan andere functies. Bekijk bijvoorbeeld onderstaande drie functies.

def herhalen(waarde, functie, aantal):
    for i in range(aantal):
        waarde = functie(waarde)
    return waarde

def verhogen(waarde):
    return waarde + 1

def verlagen(waarde):
    return waarde - 1

Hieronder staat een voorbeeld van hoe deze functies gebruikt kunnen worden. Ga na hoe Python reageert als je achtereenvolgens de volgende instructies uitvoert binnen een interactieve Python sessie waarin je eerst zorgt dat bovenstaande functies gedefinieerd werden. Verzeker jezelf ervan dat je goed begrijpt waarom je een bepaalde waarde krijgt en wat er juist gebeurt in de interactieve sessie vooraleer je verder gaat met de eigenlijke opgave.

>>> verhogen(5)
>>> verlagen(101)
>>> herhalen(5, verhogen, 3)
>>> herhalen(5, verlagen, 3)
>>> herhalen(5, verlagen, verhogen(3))

Opgave

Schrijf drie functies blok, driehoek en gauss, die een implementatie vormen van de corresponderende signaalfuncties omschreven in de inleiding van deze opgave. Aan elke functie moeten twee argumenten doorgegeven worden: een afstand $$r$$ tussen een zendmast en een ontvangstpunt, en de sterkte $$\alpha$$ van de zendmast. Elke functie moet als resultaat de corresponderende ontvangststerkte teruggeven, als een reëel getal tussen 0 en 1.
Schrijf een functie ontvangstkwaliteit die de gemiddelde ontvangstkwaliteit teruggeeft, gemeten over een reeks ontvangstpunten. De functie heeft twee verplichte parameters zendmasten en ontvangstpunten waaraan respectievelijk een lijst van coördinaten van zendmasten en een lijst van coördinaten van ontvangstpunten moeten doorgegeven worden. Elke coördinaat wordt daarbij voorgesteld als een tuple $$(x, y)$$. De functie heeft ook twee optionele parameters. Een parameter alfa die de sterkte $$\alpha$$ van de zendmasten (standaardwaarde 5.0) aangeeft, en een parameter signaalfunctie waaraan een signaalfunctie $$f(r, \alpha)$$ kan doorgegeven worden die het type van de zendmasten modelleert (standaard worden zendmasten gebruikt met een blokvormige sterkte).

Voorbeeld

>>> blok(1.0, 2.0)
1.0
>>> driehoek(1.0, 2.0)
0.5
>>> gauss(1.0, 2.0)
0.8824969025845955

>>> zendmasten = [(0.0, 0.0), (5.0, 5.0), (3.0, 4.0)]
>>> ontvangstpunten = [(1.2, 4.3), (2.8, 3.3), (3.2, 0.7), (-1.0, -1.0), (10.0, 0.0)]
>>> ontvangstkwaliteit(zendmasten, ontvangstpunten)
0.8
>>> ontvangstkwaliteit(zendmasten, ontvangstpunten, alfa=3.0)
0.6
>>> ontvangstkwaliteit(zendmasten, ontvangstpunten, signaalfunctie=driehoek)
0.5102911527511019
>>> ontvangstkwaliteit(zendmasten, ontvangstpunten, signaalfunctie=gauss)
0.8121116675748477

Hieronder zie je een kaartje dat de situatie toont voor het eerste geval in de bovenstaande doctest. Nadat je je oplossing hebt ingediend, kan je ook zo'n kaartjes bekijken om je te helpen bij het debuggen. Door te klikken op de ontvangstpunten of de zendmasten krijg je extra informatie te zien.