Je kan een homothetische matrix ook terug gaan inkrimpen. Onderstaande kan je terug inkrimpen met factor 3.

Homothetie met factor 3.

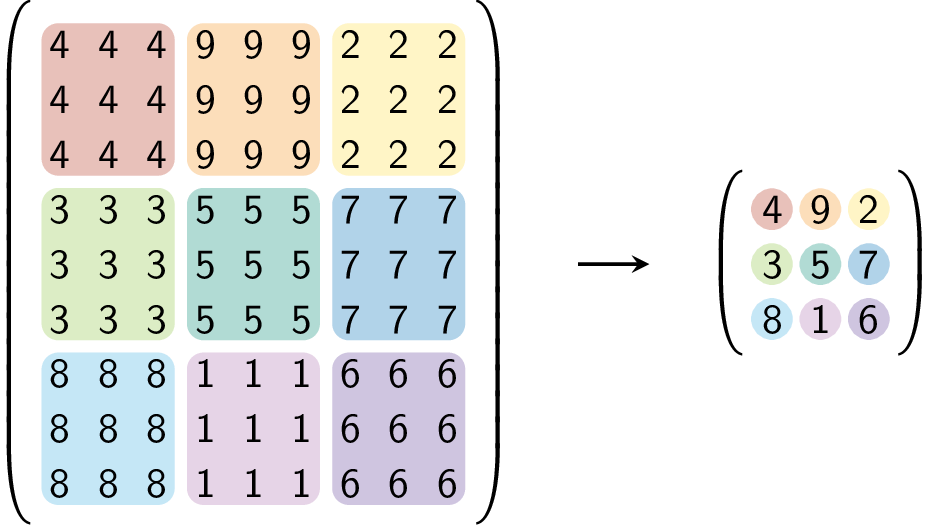
Gevraagd

Om deze oefening op te lossen schrijf je twee functies.

Schrijf eerst een functie bepaal_factor(matrix) die gegeven een matrix op zoek gaat naar de factor (k ⩾ 1) waarmee de matrix vergroot werd. Je retourneert dus het gehele getal k. Je mag ervan uit gaan dat de oorspronkelijke matrix uit verschillende gehele getallen werd opgebouwd, er zullen dus geen gelijke ‘blokken’ zijn.
Schrijf een functie inkrimpen(matrix) die de homothetische matrix gaat inkrimpen. Maak in deze functie gebruik van de vorige functie.

Bestudeer grondig onderstaande voorbeelden.

Voorbeeld 1

>>> bepaal_factor([[4, 4, 4, 9, 9, 9, 2, 2, 2],
                   [4, 4, 4, 9, 9, 9, 2, 2, 2],
                   [4, 4, 4, 9, 9, 9, 2, 2, 2],
                   [3, 3, 3, 5, 5, 5, 7, 7, 7],
                   [3, 3, 3, 5, 5, 5, 7, 7, 7],
                   [3, 3, 3, 5, 5, 5, 7, 7, 7],
                   [8, 8, 8, 1, 1, 1, 6, 6, 6],
                   [8, 8, 8, 1, 1, 1, 6, 6, 6],
                   [8, 8, 8, 1, 1, 1, 6, 6, 6]])
3

>>> inkrimpen([[4, 4, 4, 9, 9, 9, 2, 2, 2],
               [4, 4, 4, 9, 9, 9, 2, 2, 2],
               [4, 4, 4, 9, 9, 9, 2, 2, 2],
               [3, 3, 3, 5, 5, 5, 7, 7, 7],
               [3, 3, 3, 5, 5, 5, 7, 7, 7],
               [3, 3, 3, 5, 5, 5, 7, 7, 7],
               [8, 8, 8, 1, 1, 1, 6, 6, 6],
               [8, 8, 8, 1, 1, 1, 6, 6, 6],
               [8, 8, 8, 1, 1, 1, 6, 6, 6]])
[[4, 9, 2],
 [3, 5, 7],
 [8, 1, 6]]

Voorbeeld 2

>>> bepaal_factor([[4, 9, 2],
                   [3, 5, 7],
                   [8, 1, 6]])
1

>>> inkrimpen([[4, 9, 2],
               [3, 5, 7],
               [8, 1, 6]])
[[4, 9, 2],
 [3, 5, 7],
 [8, 1, 6]]